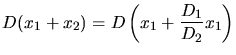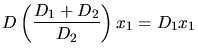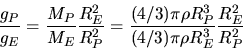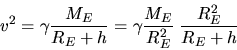Lösungen zur Übung Nr.4
Besprechung: Donnerstag, d. 17. November 2005
Aufgabe 1:
a) Die Feder wird in zwei gleich lange Teile unterteilt.
Abbildung 1:
Hintereinanderschaltung zweier Federn
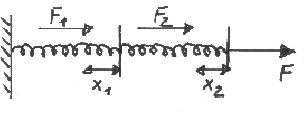 |
An beiden Federn wirkt jetzt die gleiche Kraft, daher
Daher folgt die Beziehung zwischen den Auslenkungen der beiden Federn:
Die Gesamtauslenkung beider Ferdern ist die Summe der Einzelauslenkungen, d.h.
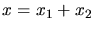 . Daher gilt:
. Daher gilt:
Zum Schluss haben wir hierbei eine Beziehung aus der ersten Gleichung benutzt. Hieraus können wir folgern:
In unserer Aufgabe ist noch speziell
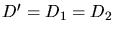 , daher
, daher 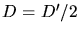 und
und 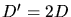 .
.
b) Jetzt kommen wir zur Parallelschaltung der beiden halben Federn.
Abbildung 2:
Parallel montierte Federn
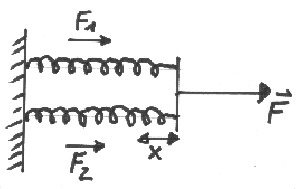 |
Übt man auf dieses System eine Kraft 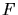 aus, so ist diese die Summe aus den Kräften an den Einzelfedern,
aus, so ist diese die Summe aus den Kräften an den Einzelfedern,
Die Federkonstante des parallel geschalteten Systems ist also
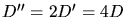 .
.
Aufgabe 2:
Während das Seil auf den Boden fällt, wirken zwei Kräfte: Erstens das Gewicht von dem bereits auf dem Boden liegenden
Teil des Seils und zweitens die durch den Impulsverlust des herunterfallenden Seils erzeugte Kraft. Wir betrachten ein
Element des Seils mit Masse 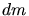 und Länge
und Länge 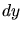 , das gerade den Boden erreicht.
Die Masse dieses Teilstücks ist
, das gerade den Boden erreicht.
Die Masse dieses Teilstücks ist 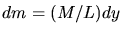 und die Kraft durch den Impulsverlust ist
und die Kraft durch den Impulsverlust ist
Hierbei ist 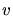 die Geschwindigkeit, mit der dieses Massenelement den Boden erreicht. Diese Geschwindigkeit ist von der
Höhe abhängig, in der das Element gestartet ist und beträgt
die Geschwindigkeit, mit der dieses Massenelement den Boden erreicht. Diese Geschwindigkeit ist von der
Höhe abhängig, in der das Element gestartet ist und beträgt 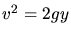 , wobei
, wobei 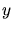 die Länge des Seilstückes
ist, das bereits auf dem Boden liegt, und daher die Fallhöhe des Seilelementes
die Länge des Seilstückes
ist, das bereits auf dem Boden liegt, und daher die Fallhöhe des Seilelementes 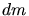 ist. Wir erhalten also
ist. Wir erhalten also
Die Gesamtkraft ergibt sich aus der Summe dieser Kraft und dem Gewicht des bereits auf dem Boden liegenden
Teil des Seilstückes:
Das Verhältnis der Gesamtkraft zu dem bereits auf dem Boden liegenden Gewicht ist also
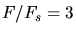 .
.
Aufgabe 3:
Die Massendichten von Erde und Planet sollten gleich sein, aslo
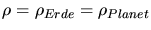 . Für die
Schwereberschleunigung an der Oberfläche des Planeten gilt dann:
. Für die
Schwereberschleunigung an der Oberfläche des Planeten gilt dann:
mit des Masse 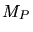 und Radius
und Radius 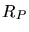 des Planeten. Für das Verhältnis der Schwerebeschleunigungen auf
Planet und Erde gilt dann
des Planeten. Für das Verhältnis der Schwerebeschleunigungen auf
Planet und Erde gilt dann
oder
Da
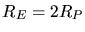 sein sollte, folgt also
sein sollte, folgt also
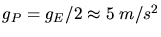 .
.
Aufgabe 4:
Wenn der Körper auf einer Kreisbahn laufen soll, muß die Radialbeschleunigung
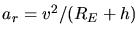 gleich der
Schwerebeschleunigung
gleich der
Schwerebeschleunigung
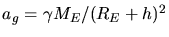 sein. Also
sein. Also
Die Geschwindigkeit folgt aus
oder
wobei also 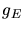 die Schwerebeschleunigung auf der Erdoberfläche ist. Einsetzen der Zahlenwerte ergibt
die Schwerebeschleunigung auf der Erdoberfläche ist. Einsetzen der Zahlenwerte ergibt
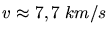
Harm Fesefeldt
2005-11-18