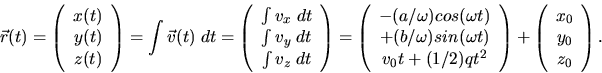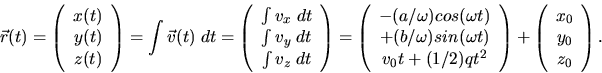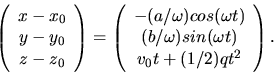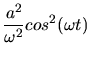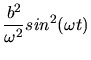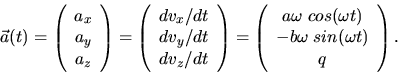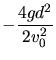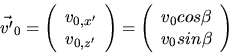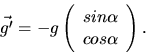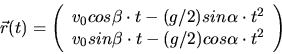Übung Nr.3
Besprechung: Donnerstag, d. 10. November 2005
Aufgabe 1:
a) Gesucht ist der Vektor
Dieses schreiben wir noch in der Form
b) Aus der vorherigen Formel ersehen wir, daß
Daher ist
Dieses ist aber nichts anderes als die Gleichung einer Ellipse mit den Achsen 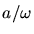 und
und 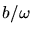 und dem Mittelpunkt
und dem Mittelpunkt
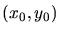 .
.
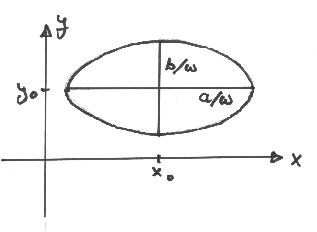
Abbildung 1:
Graphische Darstellung einer Ellipse
 |
c) Für die Beschleunigung müssen wir die Geschwindigkeit nach der Zeit ableiten:
Aufgabe 2:
Zur Lösung nehmen wir das Haus 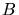 einfach weg. Wir erhalten dann eine Wurfparabel, die bei
einfach weg. Wir erhalten dann eine Wurfparabel, die bei 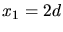 den Wert
den Wert 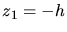 haben
muß.
haben
muß.
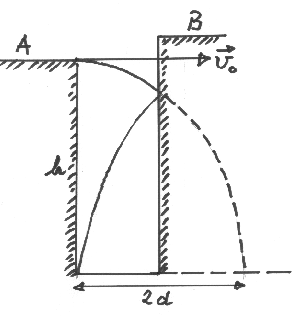
Abbildung 2:
Wurfparabel mit horizontaler Anfangsgeschwindigkeit
 |
Mit Formel (15) aus den Skript Teil 3 erhalten wir (beachte 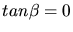 und
und 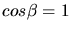 )
)
und
Aufgabe 3:
Diese Aufgabe kann auf zwei verschiedenen Wegen gelöst werden. Man könnte einmal die im Skript Kap.3, Formel (15) angegebene
Bahnkurve
verwenden. Man beachte allerdings, daß wir den Winkel 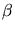 in der Formel im Skript durch den Winkel
in der Formel im Skript durch den Winkel
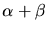 ersetzen
mußten. Weiter kann man den Schnittpunkt
ersetzen
mußten. Weiter kann man den Schnittpunkt
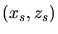 dieser Wurfparabel mit der Geraden
dieser Wurfparabel mit der Geraden
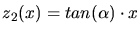 bestimmen.
Die Wurfweite ist dann
bestimmen.
Die Wurfweite ist dann
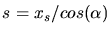 . Wir wollen die Rechnung hier nicht durchziehen, da man auf mühsame trigonometrische
Audrücke geführt wird. Eleganter und einfacher ist die folgende Lösung:
. Wir wollen die Rechnung hier nicht durchziehen, da man auf mühsame trigonometrische
Audrücke geführt wird. Eleganter und einfacher ist die folgende Lösung:
Wir führen ein neues Bezugssystem ein, bei dem die 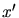 - Achse entlang des Abhanges zeigt und
- Achse entlang des Abhanges zeigt und 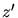 senkrecht dazu steht.
senkrecht dazu steht.
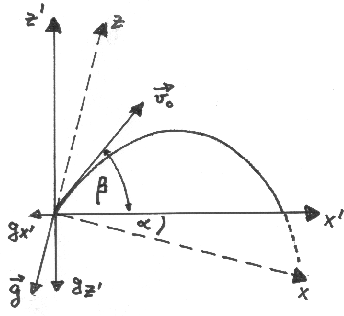
Abbildung 3:
Rotation des Bezugssystems
 |
In der folgenden Rechnung bedeutet der Strich also keine Ableitungen, sondern die physikalischen Größen im gedrehten System.
Die Geschwindigkeit des Balles beim Abschuss ist jetzt (die 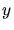 - Komponenten schreiben wir nicht mit):
- Komponenten schreiben wir nicht mit):
und die Gravitationsbeschleunigung
Die Gleichung (13) im Skript verändert sich zu
Der Ball trifft wieder auf den Abhang, wenn 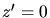 wird. Daraus folgt die Zeit
wird. Daraus folgt die Zeit 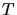 bis zum Auftreffen:
bis zum Auftreffen:
Diese Zeit setzen wir in die 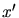 - Komponente der Bahnkurve ein und erhalten sofort
- Komponente der Bahnkurve ein und erhalten sofort
Da wir gleich noch nach 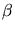 ableiten wollen, schreiben wir übersichtlicher (man beachte
ableiten wollen, schreiben wir übersichtlicher (man beachte
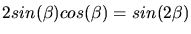 )
)
Die maximale Weite erhält man aus der Extremalbedingung
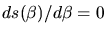 ,
,
oder auch
Daraus folgt die einfache Bedingung:
Diese Gleichung wir gelöst durch
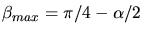 (siehe Bronstein, Taschenbuch der Mathematik).
Der Abschusswinkel mit maximaler Weite ist also
(siehe Bronstein, Taschenbuch der Mathematik).
Der Abschusswinkel mit maximaler Weite ist also
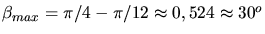 .
.
Harm Fesefeldt
2005-11-11