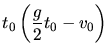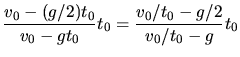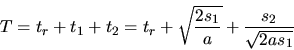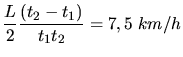Lösungen zur Übung Nr.2
Besprechung: Donnerstag, d. 3. November 2005
Aufgabe 1:
Mit dem Index 1 bezeichnen wir alle Koordinaten des ersten Steines, mit dem Index 2 die des zweiten. Die Orts- Zeit- Funktionen
lauten dann:
Hierbei ist 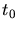 die Zeit, die der zweite Stein später gestartet ist,
die Zeit, die der zweite Stein später gestartet ist, 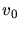 seine Anfangsgeschwindigkeit.
Beide sind am gleichen Ort, wenn
seine Anfangsgeschwindigkeit.
Beide sind am gleichen Ort, wenn 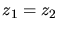 ist, d.h.
ist, d.h.
Diese Gleichung muß nach 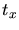 aufgelöst werden:
aufgelöst werden:
In der letzten Schreibweise sieht man sehr schön, daß es im Wesentlichen auf das Verhältnis 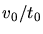 ankommt.
Mit den angegebenen Zahlenwerten
ankommt.
Mit den angegebenen Zahlenwerten
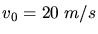 ,
,
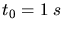 und
und
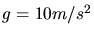 folgt die
Zeit
folgt die
Zeit
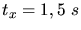 . Die beiden Steine kreuzen sich nur dann, wenn
. Die beiden Steine kreuzen sich nur dann, wenn
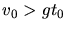 ist. Im Falle
ist. Im Falle
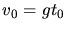 wird die Zeit Unendlich, für
wird die Zeit Unendlich, für
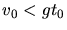 wird sie negativ.
wird sie negativ.
b) Der Überholvorgang findet bei einer Tiefe von
statt.
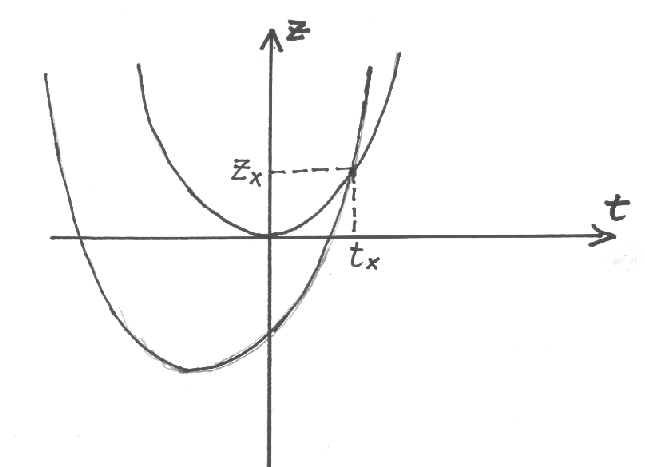
c) Beide Orts- Zeit- Funktionen sind Parabeln und nach oben geöffnet.
Abbildung 1:
Die beiden Parabeln im Vergleich
 |
Aufgabe 2:
Die Beschleunigungsstrecke
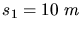 und die Strecke mit gleichbleibender Geschwindigkeit
und die Strecke mit gleichbleibender Geschwindigkeit
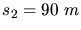 können wir mit den jeweiligen Zeiten
können wir mit den jeweiligen Zeiten 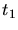 und
und 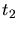 schreiben:
schreiben:
Hierbei ist also 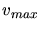 die Geschwindigkeit am Ende der Beschleunigungsstrecke. Dieses Gleichungssystem können wir
nach
die Geschwindigkeit am Ende der Beschleunigungsstrecke. Dieses Gleichungssystem können wir
nach 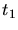 und
und 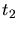 auflösen:
auflösen:
Ausserdem braucht der Läufer noch die Reaktionszeit 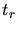 . Somit ist die Gesamtzeit
. Somit ist die Gesamtzeit 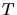 gegeben durch
gegeben durch
Einsetzen der gegebenen Zahlenwerte liefert:
Die Gesamtzeit bleibt also unter 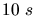 , sofern die Reaktionszeit
, sofern die Reaktionszeit
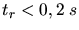 ist.
ist.
Aufgabe 3:
Sei 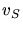 die Geschwindigkeit des Stromes und
die Geschwindigkeit des Stromes und 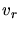 die Geschwindigkeit des Dampfers relativ zum Wasser. Dann sind
die Geschwindigkeiten
die Geschwindigkeit des Dampfers relativ zum Wasser. Dann sind
die Geschwindigkeiten 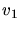 und
und 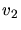 relativ zum Ufer auf der Hin- bzw. Rückfahrt:
relativ zum Ufer auf der Hin- bzw. Rückfahrt:
Mit
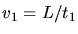 und
und
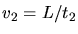 folgt:
folgt:
Dieses Gleichunfgssystem lösen wir nach 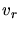 und
und 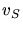 auf:
auf:
Die Durchschnittsgeschwindigkeit ist
Aufgabe 4; (Knobelaufgabe)
Zur Lösung der Aufgabe klappen wir die Seitenwände des Aquariums einfach auf (vergessen Sie aber nicht, vorher das Wasser
herauszulassen !!):
Abbildung:
Aquarium mit zwei aufgeklappten Wänden
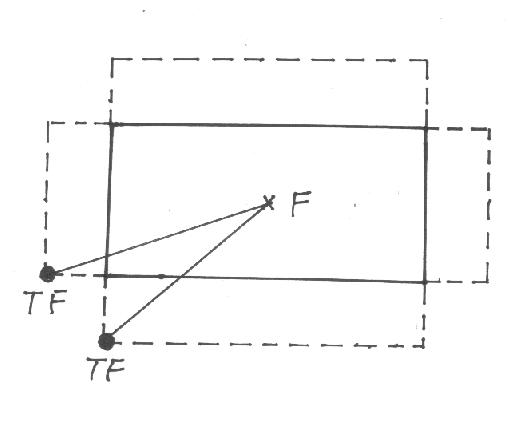 |
Wir erhalten dann zwei Möglichkeiten, um auf einem geraden Weg vom Schlafplatz 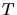 zum Futternapf
zum Futternapf 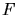 zu kommen, von denen der
Weg
zu kommen, von denen der
Weg 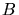 mit
mit 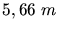 offensichtlich der kürzere ist. Dafür braucht er die Zeit
offensichtlich der kürzere ist. Dafür braucht er die Zeit
Harm Fesefeldt
2005-11-04