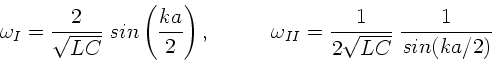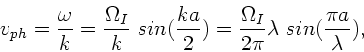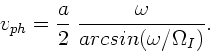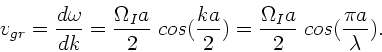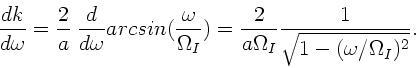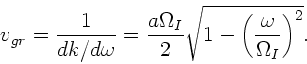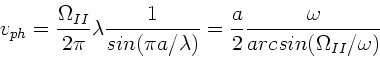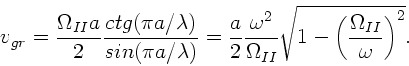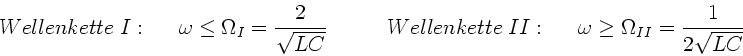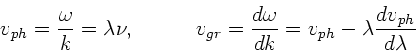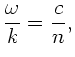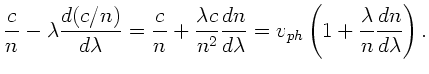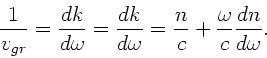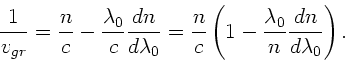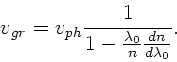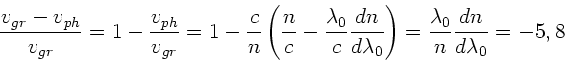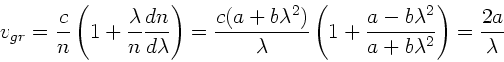Weitere Aufgaben
Aufgabe 1: (8 Punkte)
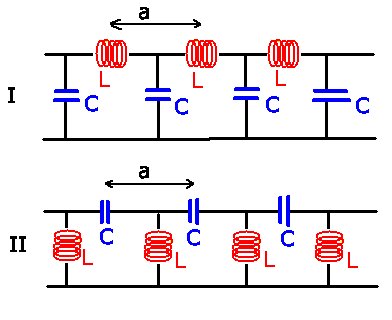
Gegeben seien die beiden folgenden Wellenketten I und II mit
unendlich vielen Gliedern, wobei 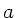 der räumliche Abstand zwischen
aufeinanderfolgenden Induktivitäten
der räumliche Abstand zwischen
aufeinanderfolgenden Induktivitäten 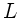 b.z.w. Kapazitäten
b.z.w. Kapazitäten 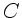 ist.
Ohmsche Widerstände können vernachlässigt werden.
ist.
Ohmsche Widerstände können vernachlässigt werden.
Man kann zeigen, daß die Dispersion in den beiden Wellenketten durch
gegeben ist (siehe z.B Berkeley Physics Course, Band 3).
a) Berechnen Sie die Phasen- und Gruppengeschwindigkeit als Funktion der
Wellenlänge 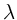 und der Frequenz
und der Frequenz 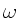 für diese beiden
Wellenketten.
für diese beiden
Wellenketten.
b) Wellen mit welchen Frequenzen werden ungedämpft durchgelassen ?
c) Wie groß ist insbesondere die Phasen- und Gruppengeschwindigkeit
der beiden Wellenleiter bei den Grenzfreqenzen
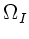 und
und 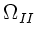 .
.
Aufgabe 2: (6 Punkte)
Gelbes Natriumlicht der Wellenlänge 589,6 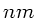 wird durch
wird durch 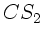 gelenkt. Der Brechungsindex bei dieser Wellenlänge beträgt
gelenkt. Der Brechungsindex bei dieser Wellenlänge beträgt 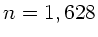 und die Dispersion
und die Dispersion
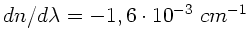 . Um
wieviel Prozent unterscheiden sich Wellen- und Gruppengeschwindigkeit ?
. Um
wieviel Prozent unterscheiden sich Wellen- und Gruppengeschwindigkeit ?
Aufgabe 3: (6 Punkte)
In einigen Tabellen wird der Brechungsindex mit
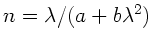 als Funktion der Wellenlänge
als Funktion der Wellenlänge 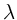 in
dem Material angegeben.
in
dem Material angegeben.
a) Wie hängt die Gruppengeschwindigkeit von dieser Wellenlänge ab ?
b) Für welchen Wellenlängenbereich kann diese Formel nur gelten ?
Lösungen
Aufgabe 1: (8 Punkte)
a) Die Phasengeschwindigkeit ist allgemein definiert als
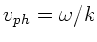 , in diesem Fall also bei der
Wellenkette I:
, in diesem Fall also bei der
Wellenkette I:
mit
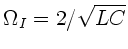 . Wegen
. Wegen
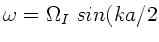 folgt
folgt
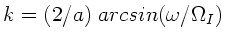 und daher auch
und daher auch
Für die Gruppengeschwindigkeit erhalten wir zunächst als Funktion
der Wellenlänge
Um 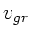 als Funktion der Frequenz zu bestimmen, bemerken wir zunächst,
daß
als Funktion der Frequenz zu bestimmen, bemerken wir zunächst,
daß
Daher folgt
Mit einer ähnlichen Rechnung folgt für den Wellenleiter II:
mit
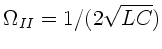 , und
, und
b) Beide Wellenketten besitzen Grenzfrequenzen, außerhalb deren
die Wellen gedämpft werden. Diesen Sachverhalt erkennt man
folgendermaßen. Falls
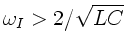 oder
oder
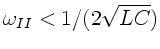 , so muß
, so muß
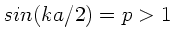 sein. Dann
ist aber
sein. Dann
ist aber 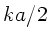 eine komplexe Zahl, d.h
eine komplexe Zahl, d.h 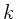 ist komplex. Setzt man
dieses in eine Lösung
ist komplex. Setzt man
dieses in eine Lösung
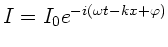 ein,
so erhält man einen Dämpfungsterm, d.h. der Strom wird gedämpft.
Die Frequenzbereiche, bei denen sich die Wellen ungedämpft fortplanzen
können, sind daher
ein,
so erhält man einen Dämpfungsterm, d.h. der Strom wird gedämpft.
Die Frequenzbereiche, bei denen sich die Wellen ungedämpft fortplanzen
können, sind daher
c) Bei den Grenzfrequenzen verschwinden in beiden Fällen die
Gruppengeschwindigkeiten, während die Phasengeschwindigkeiten
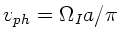 für die Wellenkette I und
für die Wellenkette I und
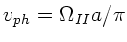 für die Wellenkette II werden.
für die Wellenkette II werden.
Vorbemerkung zu Aufgabe 2 und 3:
Zwischen 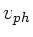 und
und 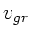 bestehen folgende Zusammenhänge:
bestehen folgende Zusammenhänge:
Für Lichtwellen gilt noch
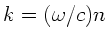 mit dem Brechungsindex
mit dem Brechungsindex 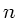 ,
wobei man beachten muß, daß
,
wobei man beachten muß, daß 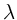 die Wellenlänge in dem
Material ist.
die Wellenlänge in dem
Material ist. 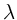 ist dann insbesondere nicht die Vakuumwellenlänge.
Phasen- und Gruppengeschwindigkeit sind
ist dann insbesondere nicht die Vakuumwellenlänge.
Phasen- und Gruppengeschwindigkeit sind
Im allgemeinen wird bei Disperionsformeln 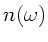 oder
oder 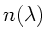 allerdings die Vakuumwellenlänge
allerdings die Vakuumwellenlänge
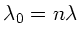 gemeint.
Dann erhalten wir eine andere Formel für die Gruppengeschwindigkeit.
Zunächst ist
gemeint.
Dann erhalten wir eine andere Formel für die Gruppengeschwindigkeit.
Zunächst ist
Wegen
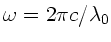 folgt
folgt
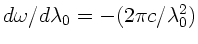 und daher
und daher
Dieses kann man auch schreiben als
Aufgabe 2: (6 Punkte)
In diesem Beispiel ist mit 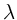 offensichtlich die
Vakuumwellenlänge gemeint. Daher
offensichtlich die
Vakuumwellenlänge gemeint. Daher
Aufgabe 3: (6 Punkte)
a) Im Gegensatz zu Aufgabe 2 ist hier ausdrücklich die Wellenlänge
in dem Material gemeint. Daher folgt mit
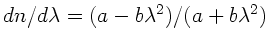 :
:
b) Damit 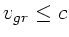 ist, muß
ist, muß
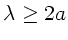 sein. Nur für diesen
Wellenlängenbereich kann diese Formel gelten.
sein. Nur für diesen
Wellenlängenbereich kann diese Formel gelten.
Harm Fesefeldt
2007-12-20