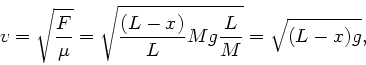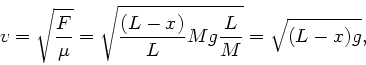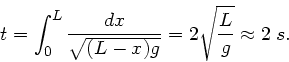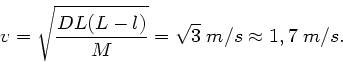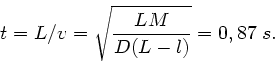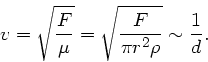Wiederholungsaufgaben
Aufgabe 1: (7 Punkte)
Ein schweres Drahtseil der Länge 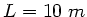 hängt unter dem
Einfluß der Schwerkraft an einem Aufhängepunkt. Das untere Ende
des Seils ist frei. Welche Zeit benötigt eine transversale Welle,
um vom befestigten Ende des Seils zum freien Ende zu gelangen ?
hängt unter dem
Einfluß der Schwerkraft an einem Aufhängepunkt. Das untere Ende
des Seils ist frei. Welche Zeit benötigt eine transversale Welle,
um vom befestigten Ende des Seils zum freien Ende zu gelangen ?
Aufgabe 2: (7 Punkte)
Eine Feder mit der Federkonstanten 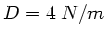 und der
Länge
und der
Länge 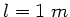 wird durch eine Kraft auf insgesamt
wird durch eine Kraft auf insgesamt
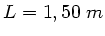 gedehnt. Die Masse der Feder beträgt
gedehnt. Die Masse der Feder beträgt 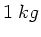 .
.
a) Wie groß ist die Phasengeschwindigkeit für eine transversale
Welle auf der Feder ?
b) Welche Zeit braucht diese Welle, um vom einen Ende der Feder zum
anderen Ende zu gelangen ?
Aufgabe 3: (6 Punkte)
Eine Guitarre hat sechs Saiten in der Tonfolge 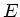 ,
, 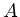 ,
, 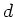 ,
, 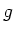 ,
,
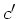 und
und 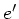 , d.h. die ersten fünf sind im Abstand von Quarten,
die letzte als große Terz gestimmt. Eine Quarte entspricht dem
Frequenzverhältnis
, d.h. die ersten fünf sind im Abstand von Quarten,
die letzte als große Terz gestimmt. Eine Quarte entspricht dem
Frequenzverhältnis
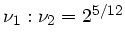 , eine große Terz
dem Verhältnis
, eine große Terz
dem Verhältnis
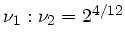 .
Berechnen Sie die notwendigen Drahtdurchmesser, wenn alle Saiten mit
der gleichen Kraft
.
Berechnen Sie die notwendigen Drahtdurchmesser, wenn alle Saiten mit
der gleichen Kraft 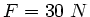 gespannt sind, die Phasengeschwindigkeiten
den Frequenzverhältnissen entsprechen sollen und der dünnste Draht
gespannt sind, die Phasengeschwindigkeiten
den Frequenzverhältnissen entsprechen sollen und der dünnste Draht
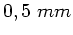 Durchmesser hat.
Durchmesser hat.
Lösungen
Aufgabe 1: (7 Punkte)
Die Phasengeschwindigkeit ist in diesem Beispiel nicht mehr
konstanr, da die Spannungskraft an einem bestimmten Punkt des
Seils durch das Gewicht des unterhalb dieses Punktes hängenden
Teilstückes 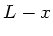 gegeben ist. Wir messen also
gegeben ist. Wir messen also 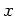 vom Aufhängepunkt
ab. Diese Kraft ist
vom Aufhängepunkt
ab. Diese Kraft ist
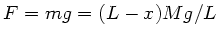 . Die Phasengeschwindigkeit
wird dann
. Die Phasengeschwindigkeit
wird dann
wobei wir für die lineare Massendichte 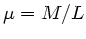 gesetzt haben.
Die Zeit zum Durchlaufen der Welle über das gesamte Seil ist dann
gesetzt haben.
Die Zeit zum Durchlaufen der Welle über das gesamte Seil ist dann
Aufgabe 2: (7 Punkte)
Wie in Aufgabe 1 ist die Phasengeschwindigkeit durch
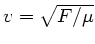 gegeben, mit der linearen Massendichte
gegeben, mit der linearen Massendichte 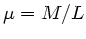 . Die Spannungskraft
ist
. Die Spannungskraft
ist 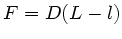 und daher
und daher
Die Zeit wird zu
Interessant ist, daß diese Zeit für eine sehr stark gespannte
Feder 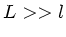 nicht mehr von
nicht mehr von 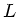 abhängt. Die Phasengeschwindigkeit
wird um denselben Betrag größer wie die Länge zunimmt.
abhängt. Die Phasengeschwindigkeit
wird um denselben Betrag größer wie die Länge zunimmt.
Aufgabe 3: (6 Punkte)
Die Phasengeschwindigkeit ist
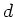 ist hierbei der Durchmasser des Drahtes. Dann folgt der Reihe nach:
ist hierbei der Durchmasser des Drahtes. Dann folgt der Reihe nach:
Harm Fesefeldt
2007-12-04