Übung Nr. 1
Abgabetermin: Mittwoch, den 8. November 2000
Aufgabe 1: (5 Punkte)
Zeigen Sie, daß die Überlagerung folgender harmonischer Wellen
mit
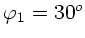 ,
,
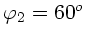 und
und
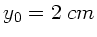 wieder eine harmonische Welle ist. Wie groß sind die Phasenkonstante und
Amplitude der resultierenden Welle ?
wieder eine harmonische Welle ist. Wie groß sind die Phasenkonstante und
Amplitude der resultierenden Welle ?
Aufgabe 2: (6 Punkte)
a) Wie lautet die eindimensionale Wellengleichung
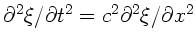 in den Koordinaten
in den Koordinaten 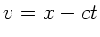 und
und 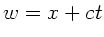 ?
?
b) Zeigen Sie, daß
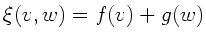 die allgemeinste Lösung dieser
Wellengleichung ist !
die allgemeinste Lösung dieser
Wellengleichung ist !
Aufgabe 3: (4 Punkte)
Ein schweres Seil der Länge 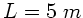 ist mit einem Ende an der Decke
eines Hörsaals befestigt und hängt unter dem Einfluß der Schwerkraft
frei herab. Wie lange dauert es, bis ein kurzer transversaler Wellenpuls
vom unteren Ende des Seils bis zur Decke und wieder zurück läuft ?
ist mit einem Ende an der Decke
eines Hörsaals befestigt und hängt unter dem Einfluß der Schwerkraft
frei herab. Wie lange dauert es, bis ein kurzer transversaler Wellenpuls
vom unteren Ende des Seils bis zur Decke und wieder zurück läuft ?
Aufgabe 4: (5 Punkte)
a) Eine Feder der Länge 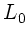 wird auf die Länge
wird auf die Länge 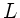 gedehnt. Die Masse
der Feder sei
gedehnt. Die Masse
der Feder sei 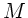 und die Federkonstante
und die Federkonstante 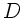 . Berechnen Sie die
Phasengeschwindigkeiten für longitudinale und transversale Wellen auf der
Feder.
. Berechnen Sie die
Phasengeschwindigkeiten für longitudinale und transversale Wellen auf der
Feder.
b) Welche Bedingung muß im Grenzfall erfüllt sein, damit beide
Phasengeschwindigkeiten von Teil a) gleich sind ?
Harm Fesefeldt
2007-11-28