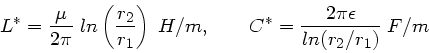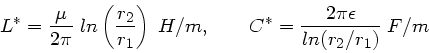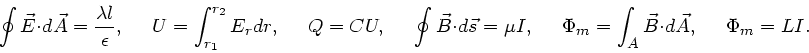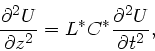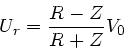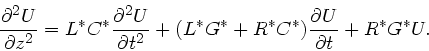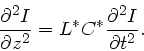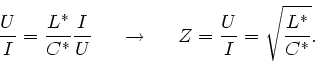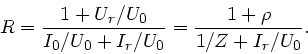Ergänzungen zur Signalübertragung auf Kabeln
Die Signalübertragung auf Kabeln ist eines der wichtigsten Gebiete
der Experimentalphysik und Informatik. Insbesondere das Koaxialkabel
gehört zum Standard eines jeden Labors.
Aufgabe 1: Zeigen Sie, daß die Induktivitätsbelegung
und Kapazitätsbelegung eines Koaxialkabels durch
gegeben sind. Zur Erinnerung seien die folgenden Formeln noch einmal
zusammengefaßt:
Im folgenden Ersatzschaltbild berücksichtigen wir neben der
Induktivitätsbelegung und der Kapazitätsbelegung noch den Omschen
Widerstand pro Längeneinheit 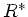 , sowie die Leitfähigkeit
pro Längeneinheit
, sowie die Leitfähigkeit
pro Längeneinheit 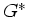 durch das Dielektrikum.
durch das Dielektrikum.
Die Differenz der Spannung und des Stromes pro Längeneinheit sind
dann durch
gegeben. Daraus folgen die beiden gekoppelten Differentialgleichungen
Aufgabe 2: Wie lautet die allgemeine Wellengleichung für die
Spannung 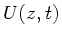 ?
?
Für das verlustfreie Kabel wird 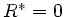 und
und
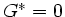 gesetzt. Dann gilt die Wellengleichung (siehe Aufgabe 2)
gesetzt. Dann gilt die Wellengleichung (siehe Aufgabe 2)
mit der Phasengeschwindigkeit
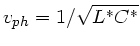 .
Für das verlustfreie Kabel (und nur für dieses) hat man also keine
Dispersion.
.
Für das verlustfreie Kabel (und nur für dieses) hat man also keine
Dispersion.
Aufgabe 3: Wie lautet die Wellengleichung für den Strom 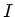 beim verlustfreien Kabel ?
beim verlustfreien Kabel ?
In der Ableitung dieser Wellengleichungen wurde die spezielle
Geometrie des Kabel nicht betrachtet. Entsprechende Gleichungen
gelten also für alle Kabel mit konstanter paralleler Geometrie,
bei denen 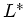 ,
, 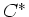 ,
, 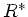 und
und 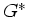 nicht von
der Ausbreitungsrichtung
nicht von
der Ausbreitungsrichtung 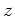 abhängen.
Die Phasengeschwingkeit ist andererseits auch durch die
Ausbreitungsgeschwindigkeit der elektromagnetischen Welle im Dielektrikum
gegeben. Diese ist aber
abhängen.
Die Phasengeschwingkeit ist andererseits auch durch die
Ausbreitungsgeschwindigkeit der elektromagnetischen Welle im Dielektrikum
gegeben. Diese ist aber
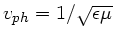 .
Daher muß auch
.
Daher muß auch
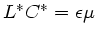 sein.
sein.
Die charakteristische Impedanz eines Kabels ist definiert durch
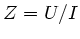 .
.
Aufgabe 4: Zeigen Sie, daß für die charakteristische Impedanz
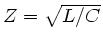 gilt.
gilt.
Typische Koaxialkabel haben eine Impedanz zwischen 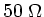 und
und
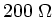 . Die allgemeine Lösung der Wellengleichung für
die Spannung ist
. Die allgemeine Lösung der Wellengleichung für
die Spannung ist
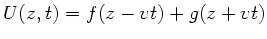 , d.h. eine
Überlagerung der einlaufenden Welle mit einer reflektierten Welle.
, d.h. eine
Überlagerung der einlaufenden Welle mit einer reflektierten Welle.
Aufgabe 5: Auf einer Leitung mit Impedanz 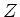 läuft ein
Spannungspuls
läuft ein
Spannungspuls 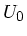 auf einen Abschlußwiderstand
auf einen Abschlußwiderstand 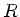 zu. Zeigen
Sie, daß der reflektierte Puls durch
zu. Zeigen
Sie, daß der reflektierte Puls durch
gegeben ist.
Wir sehen also, daß man einen reflektionsfreien Abschluß nur für
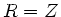 erhält (siehe auch Aufgabe 3 der Heimübungen). Weitere
Anwendungen dieser Formel sind in der folgenden ehemaligen
Klausuraufgabe gegeben:
erhält (siehe auch Aufgabe 3 der Heimübungen). Weitere
Anwendungen dieser Formel sind in der folgenden ehemaligen
Klausuraufgabe gegeben:
Aufgabe 6: Zwei Koaxialkabel mit den Impedanzen 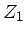 und
und
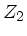 sollen miteinander verbunden werden. Ein Signal wird vom ersten
Leiter in den zweiten Leiter geschickt. Damit keine Reflexionen
auftreten, müssen Sie die Verbindungsstelle mit einem ohmschen
Widerstand
sollen miteinander verbunden werden. Ein Signal wird vom ersten
Leiter in den zweiten Leiter geschickt. Damit keine Reflexionen
auftreten, müssen Sie die Verbindungsstelle mit einem ohmschen
Widerstand 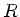 in einer geeigneten Scahltung überbrücken.
Wie sieht die Schaltung aus und wie groß muß der Widerstand
in einer geeigneten Scahltung überbrücken.
Wie sieht die Schaltung aus und wie groß muß der Widerstand 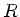 sein, wenn a)
sein, wenn a) 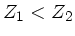 und b)
und b) 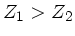 ist ?
ist ?
Lösungen
Aufgabe 2: Einsetzen von
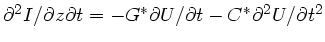 und
und
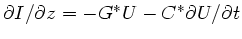 in die
Gleichung
in die
Gleichung
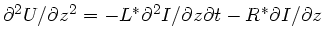 liefert die Wellengleichung
liefert die Wellengleichung
Der Term
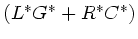 ist offensichtlich ein Dämpfungsterm.
ist offensichtlich ein Dämpfungsterm.
Aufgabe 3: Die Herleitung ist exakt gleich der Herleitung in
Aufgabe 2, nur das 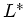 und
und 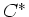 bzw
bzw 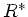 und
und 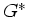 vertauscht werden müssen.
Dieses führt aber zum gleichen Endergebnis. Daher (für das verlustfreie
Kabel):
vertauscht werden müssen.
Dieses führt aber zum gleichen Endergebnis. Daher (für das verlustfreie
Kabel):
Aufgabe 4: Wir nehmen eine Lösung
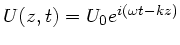 und
und
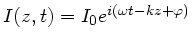 , wobei der Strom
also phasenverschoben gegenüber der Spannung sein kann. Dann ist
, wobei der Strom
also phasenverschoben gegenüber der Spannung sein kann. Dann ist
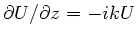 ,
,
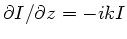 ,
,
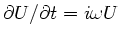 und
und
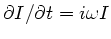 . Einsetzen dieser Ausdrücke in
. Einsetzen dieser Ausdrücke in
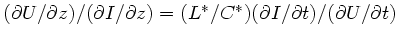 ergibt:
ergibt:
Aufgabe 5: Für den einlaufenden Puls gilt
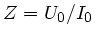 ,
für den reflektierten entsprechend
,
für den reflektierten entsprechend
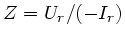 . Ströme
haben eine Richtung, daher ein Minuszeichen ! Im Widerstand gilt
. Ströme
haben eine Richtung, daher ein Minuszeichen ! Im Widerstand gilt
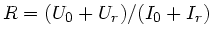 . Zusatzfrage: Warum warum muß
der reflektierte Strom hier positiv eingesetzt werden ? Aus der letzten
Formel erhalten wir mit dem Reflexionskoeffizienten
. Zusatzfrage: Warum warum muß
der reflektierte Strom hier positiv eingesetzt werden ? Aus der letzten
Formel erhalten wir mit dem Reflexionskoeffizienten
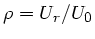 :
:
Wegen
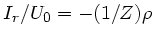 folgt
folgt
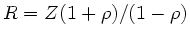 .
Dieser Ausdruck kann in bekannter Weise umgeformt werden in
.
Dieser Ausdruck kann in bekannter Weise umgeformt werden in
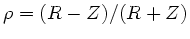 .
.
Aufgabe 6:
a) Wenn 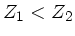 ist, so sieht das Signal eine größere
Impedanz. Die Impedanz muß also reduziert werden. Dieses erreicht man durch
eine Parallelschaltung des Widerstandes
ist, so sieht das Signal eine größere
Impedanz. Die Impedanz muß also reduziert werden. Dieses erreicht man durch
eine Parallelschaltung des Widerstandes 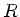 .
.
Dann folgt
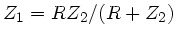 und
und
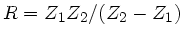 .
.
b) Im Fall 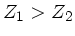 muß die Impedanz vergrößert werden, daher
benötigt man eine Serienschaltung:
muß die Impedanz vergrößert werden, daher
benötigt man eine Serienschaltung:
In diesem gilt also:
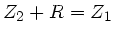 und
und
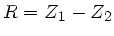 .
.
Harm Fesefeldt
2007-12-19