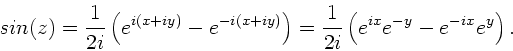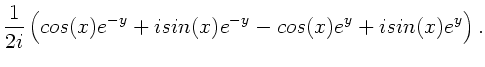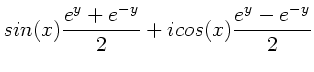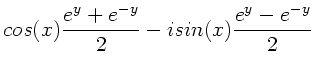Rechenübungen am 25. Oktober 2000
Aufgabe 1:
Gegeben sei eine harmonische Schallwelle der Form
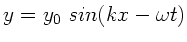 mit der Frequenz
mit der Frequenz
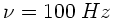 und Schallgeschwindigkeit
und Schallgeschwindigkeit 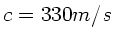 . Berechnen Sie die a) Kreisfrequenz
. Berechnen Sie die a) Kreisfrequenz
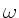 , b) Wellenlänge
, b) Wellenlänge  , c) Schwingungsdauer
, c) Schwingungsdauer 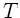 und
d) Wellenzahl
und
d) Wellenzahl 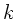 . e) Wie sieht die Funktion aus, wenn sich die Welle in
entgegengesetzter Richtung fortpflanzt ?
. e) Wie sieht die Funktion aus, wenn sich die Welle in
entgegengesetzter Richtung fortpflanzt ?
Aufgabe 2:
Eine bestimmte Welle kann durch den Ausdruck
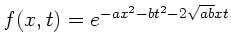 beschrieben werden
(
beschrieben werden
(
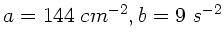 ).
).
a) In welche Richtung läuft diese Welle ?
b) Wie groß ist die Phasengeschwindigkeit ?
c) Skizzieren Sie die Welle zur Zeit 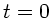 und
und 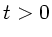 .
.
d) Erfüllt diese Welle die Wellengleichung ?
e) Handelt es sich hierbei um eine harmonische Welle ?
Aufgabe 3:
Gegeben sei das Wellenpaket
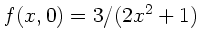 zur Zeit
zur Zeit 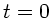 .
Wie lauten die Wellen mit diesem Profil, die sich mit der Geschwindigkeit
.
Wie lauten die Wellen mit diesem Profil, die sich mit der Geschwindigkeit
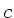 in positiver und negativer
in positiver und negativer 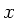 - Richtung bewegen ?
- Richtung bewegen ?
Aufgabe 4:
Zeigen Sie, daß
 Lösungen der
Wellengleichung sind.
Lösungen der
Wellengleichung sind.
Aufgabe 5:
Leiten Sie die Beziehungen
aus der Eulerschen Formel
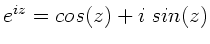 ab.
ab.
Aufgabe 6:
Schreiben Sie die Funktionen 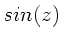 und
und 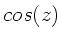 als Summe ihrer Real-
und Imaginärteile.
als Summe ihrer Real-
und Imaginärteile.
Aufgabe 7:
Beweisen Sie, daß die Multiplikation einer harmonischen Welle mit  mit einer Phasenverschiebung um
mit einer Phasenverschiebung um 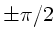 gleichwertig ist.
gleichwertig ist.
Aufgabe 8:
Wir betrachten zwei Wellen
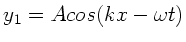 und
und
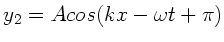 . Mit komplexer Schreibweise
zeige man, daß die Überlagerung beider Wellen eine stehende Welle
. Mit komplexer Schreibweise
zeige man, daß die Überlagerung beider Wellen eine stehende Welle
 ergibt.
ergibt.
Lösungen
Aufgabe 1:
a)
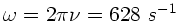
b)
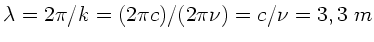
c)
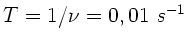
d)
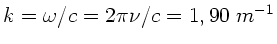
e)
 .
.
Aufgabe 2:
a) Wegen
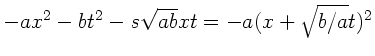 kann man diesen Wellenpuls auch schreiben als
kann man diesen Wellenpuls auch schreiben als
Die Welle läuft als in negativer 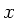 - Richtung.
- Richtung.
b) Die Phasengeschwindigkeit ist
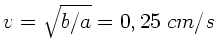 .
.
c)
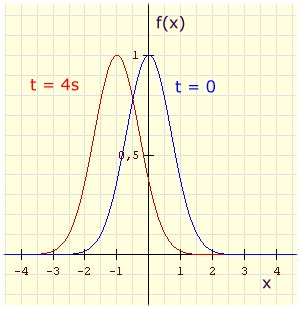
d) Jede Funktion 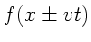 erfüllt die Wellengleichung
erfüllt die Wellengleichung
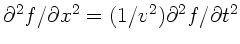 .
.
Es handelt sich nicht um eine harmonische Welle, sondern um eine Summe
(unendlich vieler) harmonischer Wellen (Fourier- Zerlegung, das kriegen wir
später).
Aufgabe 3:
![$f(x,t) = 3/[2(x \pm ct)^{2} + 1]$](img35.gif) , wobei das negative Vorzeichen für
die Ausbreitung in positiver Richtung und das positive Vorzeichen für die
Ausbreitung in negativer Richtung gilt.
, wobei das negative Vorzeichen für
die Ausbreitung in positiver Richtung und das positive Vorzeichen für die
Ausbreitung in negativer Richtung gilt.
Aufgabe 4:
Die ersten und zweiten partiellen Ableitungen der Funktion sind:
Einsetzen dieser Ausdrücke in die Wellengleichung beweist die angegebene
Behauptung.
Aufgabe 5:
Wir schreiben
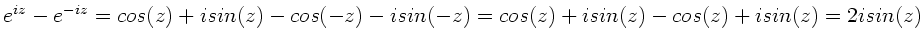 oder
oder
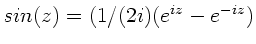 . Entsprechend für die zweite
Gleichung.
. Entsprechend für die zweite
Gleichung.
Aufgabe 6:
Wir verwenden die Formeln der vorherigen Aufgabe 5 und setzen auf der
rechten Seite 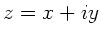 mit reellem
mit reellem 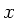 und
und 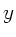 .
.
Für 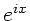 und
und 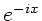 verwenden wir wiederum die Eulerschen Formeln
und erhalten
verwenden wir wiederum die Eulerschen Formeln
und erhalten
Sortieren nach 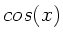 und
und 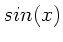 ergibt dann
ergibt dann
Aufgabe 7:
Sei
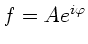 , dann ist
, dann ist
 .
Wegen
.
Wegen
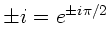 folgt
folgt
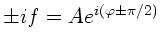 .
.
.
Aufgabe 8:
Die Überlagerung lautet in komplexer Schreibweise
![$y = A e^{ikx}[e^{i\omega t} + e^{-i \omega t} e^{i \pi}]$](img64.gif) . Wegen
. Wegen
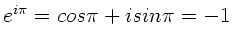 folgt
folgt
![$y = A e^{ikx} [ e^{i\omega t} - e^{-i\omega t}]
= A e^{ikx} 2i \; sin(\omega t)$](img66.gif) . Anwendung der Eulerschen Formel auf
. Anwendung der Eulerschen Formel auf
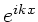 ergibt
ergibt
![$y = A[2i \; cos(kx) sin(\omega t) - 2 sin(kx)sin(\omega t)]$](img68.gif) .
Der Realteil dieses Ausdrucks ist
.
Der Realteil dieses Ausdrucks ist
 .
.
Harm Fesefeldt
2007-11-30
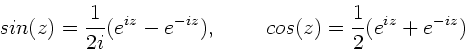
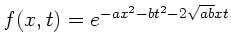 beschrieben werden
(
beschrieben werden
(
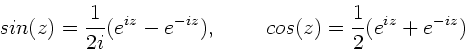
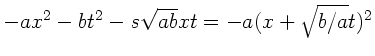 kann man diesen Wellenpuls auch schreiben als
kann man diesen Wellenpuls auch schreiben als
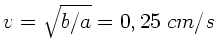 .
. 
![]() erfüllt die Wellengleichung
erfüllt die Wellengleichung
![]() .
.
![]() , wobei das negative Vorzeichen für
die Ausbreitung in positiver Richtung und das positive Vorzeichen für die
Ausbreitung in negativer Richtung gilt.
, wobei das negative Vorzeichen für
die Ausbreitung in positiver Richtung und das positive Vorzeichen für die
Ausbreitung in negativer Richtung gilt.