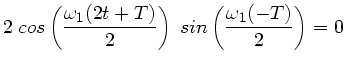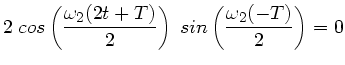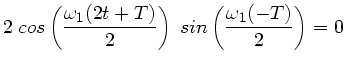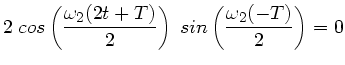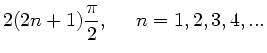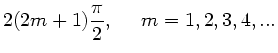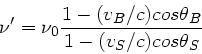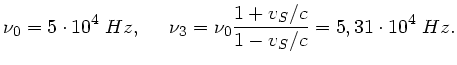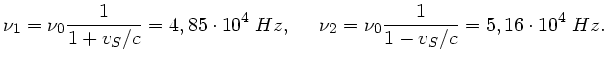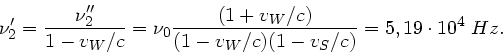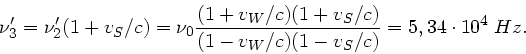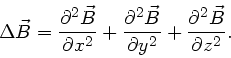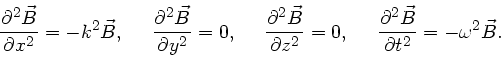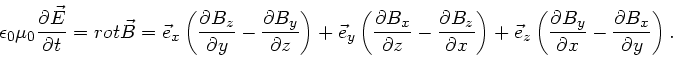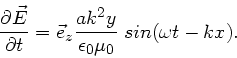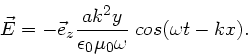Lösungsvorschläge zur Übung Nr. 4
Besprechung: Mittwoch, den 29. November 2000
Aufgabe 1: (6 Punkte)
Sei
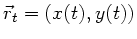 der Bahnpunkt zur Zeit
der Bahnpunkt zur Zeit 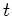 , so muß es
bei einer periodischen Bahn einen späteren Zeitpunkt
, so muß es
bei einer periodischen Bahn einen späteren Zeitpunkt 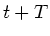 mit
konstantem
mit
konstantem 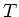 geben, für den
geben, für den
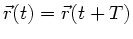 oder auch
oder auch
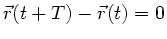 gilt.
Die letzte Gleichung können wir mit Hilfe trigonometrischer Formeln
schreiben als
gilt.
Die letzte Gleichung können wir mit Hilfe trigonometrischer Formeln
schreiben als
Diese Bedingungen sind erfüllt, wenn gleichzeitig
Daher muß
eine rationale Zahl sein. Die obigen Bedingsgleichungen sind auch
erfüllt, wenn
Die Zahlen
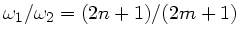 sind allerdings
in der ersten Lösung bereits enthalten.
sind allerdings
in der ersten Lösung bereits enthalten.
Aufgabe 2: (7 Punkte)
Wir gehen von der in der Vorlesung angegebenen Formel
aus.
a) Die Geschwindigkeit der Fledermaus 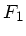 ist
ist
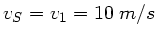 und ihre Senderfrequenz
und ihre Senderfrequenz
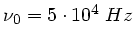 . Betrachten wir zunächst die
Fledermaus
. Betrachten wir zunächst die
Fledermaus 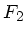 . Sie bewegt sich nicht, also ist
. Sie bewegt sich nicht, also ist 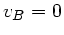 . Sie hört einmal
die direkt von
. Sie hört einmal
die direkt von 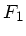 kommenden Frequenzen. Diese sind wegen
kommenden Frequenzen. Diese sind wegen
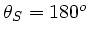 und damit
und damit
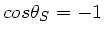 durch
durch
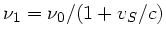 gegeben. Die Wand wirkt als Empfänger der Frequenz
gegeben. Die Wand wirkt als Empfänger der Frequenz
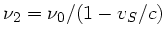 . In diesem Fall ist ebenfalls
. In diesem Fall ist ebenfalls 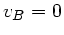 , aber
, aber
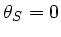 und damit
und damit
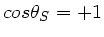 . Diese Wellen werden reflektiert
und ebefalls von
. Diese Wellen werden reflektiert
und ebefalls von 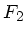 empfangen. Die Fledermaus
empfangen. Die Fledermaus 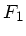 hört einmal die
Frequenz
hört einmal die
Frequenz 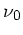 in ihrem eigenen Ruhesystem. Zum anderen hört sie die von der Wand
reflektierten Wellen, allerdings als Beobachter mit der Geschwindigkeit
in ihrem eigenen Ruhesystem. Zum anderen hört sie die von der Wand
reflektierten Wellen, allerdings als Beobachter mit der Geschwindigkeit
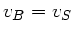 und
und
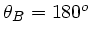 oder
oder
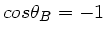 , d.h.
, d.h.
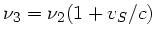 . Zusammngefaßt erhalten wir:
. Zusammngefaßt erhalten wir:
b) Die Frequenzen 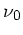 und
und 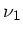 ändern sich nicht. Die Wand mit
ändern sich nicht. Die Wand mit
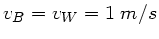 wirkt jetzt als Empfänger der Frequenz
wirkt jetzt als Empfänger der Frequenz
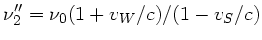 und als Sender der Frequenz
und als Sender der Frequenz
Daraus folgt für die Grequenz 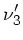 :
:
Die Änderungen sind also sehr klein, trotzdem können Fledermäuse
diese wahrnehmen.
Aufgabe 3: (7 Punkte)
a) Nach Vorlesung ergibt die Anwendung des Laplace- Operators auf einen Vector
Obwohl die 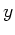 - Komponente des
- Komponente des 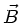 - Feldes ausser von
- Feldes ausser von
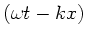 noch von
noch von 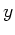 abhängt, ist trotzdem
abhängt, ist trotzdem
Einsetzen in die Wellengleichung ergibt
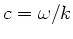 ist aber die Phasengeschwindigkeit der elektromagnetischen
Wellen.
ist aber die Phasengeschwindigkeit der elektromagnetischen
Wellen.
b) Im freien Raum (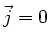 ) lautet die vierte Maxwellsche Gleichung
) lautet die vierte Maxwellsche Gleichung
Die einzig nicht verschwindende Ableitung ist im vorliegenden Problem
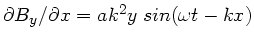 . Daher folgt
. Daher folgt
Integration über die Zeit liefert bei Vernachlässigung der
Integrationskonstanten
Harm Fesefeldt
2007-12-14