Übung Nr.11
Abgabetermin: Montag, d. 11. Juli 2005
Aufgabe 1: (5 Punkte)
a) Beim Natrium beträgt die Fermi- Energie
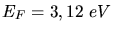 und die Dichte
und die Dichte
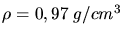 . Berechnen Sie aus diesen Angaben die Anzahl der Leitungselektronen
pro Atom.
. Berechnen Sie aus diesen Angaben die Anzahl der Leitungselektronen
pro Atom.
b) Berechnen Sie den Anteil der Leitungselektronen in Natrium, deren Energien bei Zimmertemperatur
größer als die Fermi- Energie 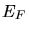 ist.
ist.
Aufgabe 2: (5 Punkte)
Berechnen Sie die mittlere Energie eines Leitungselektrons in Natrium bei niedrigen
Temperaturen (
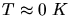 ).
).
Aufgabe 3: (5 Punkte)
Legt man an ein Metall ein Magnetfeld an, so stellen sich die Spins der Leitungselektronen parallel
bzw. antiparallel zum Feld ein. Man erhält dann verschiedene Zustandsdichten
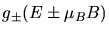 für die Elektronen der beiden Spinstellungen
(siehe Abbildung unten auf dieser Seite). Berechnen Sie
hieraus die paramagnetische Suszeptibilität von Kupfer (
für die Elektronen der beiden Spinstellungen
(siehe Abbildung unten auf dieser Seite). Berechnen Sie
hieraus die paramagnetische Suszeptibilität von Kupfer (
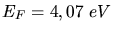 ) bei niedrigen Temperaturen.
(Anmerkung: Beachten Sie bei der Lösung, daß für fast alle Energien und technisch
herstellbare Magnetfelder
) bei niedrigen Temperaturen.
(Anmerkung: Beachten Sie bei der Lösung, daß für fast alle Energien und technisch
herstellbare Magnetfelder
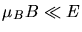 ist, in der Abbildung ist
ist, in der Abbildung ist 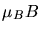 viel zu groß gezeichnet).
viel zu groß gezeichnet).
Aufgabe 4: (5 Punkte)
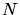 unterscheidbare Atome sind auf zwei Energieniveaus
unterscheidbare Atome sind auf zwei Energieniveaus 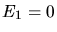 und
und 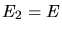 verteilt.
Die Energieniveaus seien nicht entartet.
verteilt.
Die Energieniveaus seien nicht entartet.
a) Zeigen Sie, daß die Energie 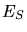 des Systems bei der Temperatur
des Systems bei der Temperatur 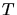 durch
durch
gegeben ist.
b) Berechnen Sie die spezifische Wärme 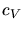 für dieses System.
für dieses System.
c) Skizzieren Sie die Lösung für 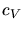 als Funktion von
als Funktion von 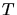 .
.
Harm Fesefeldt
2005-07-05