Übung Nr.4
Abgabetermin: Montag, d. 23. Mai 2005
Aufgabe 1: (5 Punkte)
Ein paralleles Bündel monoenergetischer Elektronen der Energie 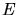 fällt senkrecht
auf einen Schirm mit einem langen Spalt der Breite
fällt senkrecht
auf einen Schirm mit einem langen Spalt der Breite 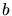 . Berechnen Sie die Verteilung
der Elektronen in der Beugungsfigur, die im Abstand
. Berechnen Sie die Verteilung
der Elektronen in der Beugungsfigur, die im Abstand 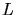 vom Schirm entsteht.
Wie groß ist insbesondere der Abstand des ersten Minimums vom Hauptmaximum.
vom Schirm entsteht.
Wie groß ist insbesondere der Abstand des ersten Minimums vom Hauptmaximum.
Aufgabe 2: (8 Punkte)
Ein Teilchen mit der Energie 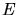 bewegt sich in einem eindimensionalen Potential
bewegt sich in einem eindimensionalen Potential 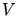 , das durch
, das durch
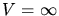 für
für 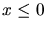 ,
, 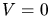 für
für 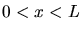 und
und 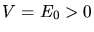 für
für
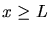 gegeben ist.
gegeben ist.
a) Zeigen Sie, daß das Teilchen im Fall 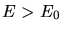 ein kontinuierliches Energiespektrum
besitzt.
ein kontinuierliches Energiespektrum
besitzt.
b) Lösen Sie die Schrödingergleichung für den Fall 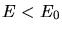 und zeigen
Sie, daß das Energiespektrum diskret ist und nur endlich viele Werte hat.
Hier genügt eine graphische Darstellung einer möglicherweise transzendenten Gleichung.
(Anleitung: Transformieren Sie die Gleichung auf eine Form
und zeigen
Sie, daß das Energiespektrum diskret ist und nur endlich viele Werte hat.
Hier genügt eine graphische Darstellung einer möglicherweise transzendenten Gleichung.
(Anleitung: Transformieren Sie die Gleichung auf eine Form
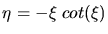 , und zwar so,
daß
, und zwar so,
daß
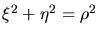 gilt, wobei
gilt, wobei 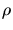 nicht mehr von
nicht mehr von 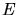 abhängt. Aus den Schnittpunkten
dieser beiden Gleichungen kann man die erlaubten Werte von
abhängt. Aus den Schnittpunkten
dieser beiden Gleichungen kann man die erlaubten Werte von 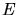 bestimmen)
bestimmen)
c) Welcher Bedingung muß 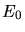 genügen, damit überhaupt diskrete Energiewerte auftreten
genügen, damit überhaupt diskrete Energiewerte auftreten ?
Vergleichen Sie Ihr Ergebnis mit der Heisenbergschen Unschärferelation.
?
Vergleichen Sie Ihr Ergebnis mit der Heisenbergschen Unschärferelation.
d) Skizzieren Sie die ersten drei Wellenfunktionen und berechnen Sie die Aufenthaltswahrscheinlichkeit
in Abhängigkeit von 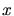 und
und 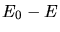 .
.
Aufgabe 3: (7 Punkte)
a) Transformieren Sie mit
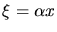 die Schrödingergleichung des eindimensionalen
harmonischen Oszillators in die Form
die Schrödingergleichung des eindimensionalen
harmonischen Oszillators in die Form
Geben Sie 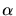 und
und 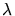 an.
an.
b) Die Eigenfunktionen haben dann die allgemeine Form
Berechnen Sie die ersten drei Eigenfunktionen (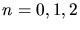 ) und
zeigen Sie, daß die Anzahl der Knoten mit
) und
zeigen Sie, daß die Anzahl der Knoten mit 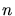 übereinstimmt.
übereinstimmt.
c) Zeigen Sie, daß die ersten beiden Eigenfunktionen orthogonal sind.
d) Berechnen Sie die Erwartungswerte 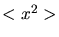 für die ersten beiden Zustände und
schreiben Sie diese Erwartungswerte als Funktion der Energie des Zustandes.
für die ersten beiden Zustände und
schreiben Sie diese Erwartungswerte als Funktion der Energie des Zustandes.
Harm Fesefeldt
2005-05-11