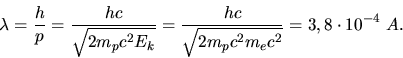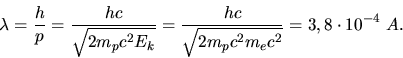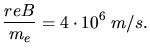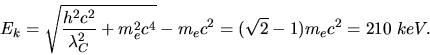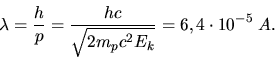Rechenübung am 3/4. Mai 2005
Relativistisch oder nichtrelativistisch, das ist hier die Frage.
Aufgabe 1:
Welche de-Broglie Wellenlänge hat ein Proton, dessen kinetische Energie gleich der
Ruheenergie eines Elektrons ist ?
Aufgabe 2:
Ein Elektron bewegt sich in einem homogenen Magnetfeld der Feldtärke
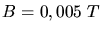 auf einer
Kreisbahn mit dem Radius
auf einer
Kreisbahn mit dem Radius 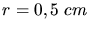 . Welche de-Broglie Wellenlänge hat das Elektron
. Welche de-Broglie Wellenlänge hat das Elektron ?
?
Aufgabe 3:
Welche kinetische Energie hat ein Elektron, dessen de-Broglie Wellenlänge gleich der
Compton- Wellenlänge ist ?
Aufgabe 4:
Berechnen Sie die de-Broglie Wellenlängen für folgende Teilchen:
a) Staubkorn mit 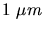 Durchmesser,
Durchmesser,
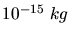 Masse und
Masse und 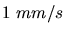 Geschwindigkeit.
Geschwindigkeit.
b) thermisches Neutron mit Ruheenergie 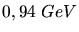 bei einer Temperatur von
bei einer Temperatur von 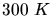 .
.
c) Elektron mit einer kinetischen Energie von 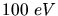 .
.
d) Elektron mit Gesamtenergie von 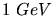 .
.
e) Proton mit kinetischer Energie von 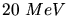 .
.
Lösungen
Aufgabe 1
Die Ruhemasse des Elektrons ist klein gegenüber der Ruhemasse des Protons. Daher
kann nichtrelativistisch gerechnet werden.
Aufgabe 2:
Aus Lorentzkraft und Zentrifugalkraft berechnen wir die Geschwindgkeit
(
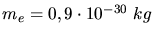 ,
,
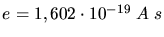 ). Das ist also
). Das ist also
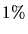 der Lichtgeschwindigkeit, also geht die Rechnung wiederum nichtrelativistisch.
der Lichtgeschwindigkeit, also geht die Rechnung wiederum nichtrelativistisch.
Mit
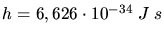 folgt
folgt
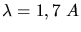 .
.
Aufgabe 3:
Da
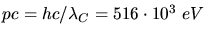 praktisch gleich der
Ruhemasse des Elektrons ist, muss relativistisch gerechnet werden.
Mit
praktisch gleich der
Ruhemasse des Elektrons ist, muss relativistisch gerechnet werden.
Mit
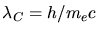 gilt
gilt
Aufgabe 4:
a) Offensichtlich nichtrelativistisch. Mit
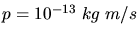 folgt
folgt
b) Auch hier natürlich nichtrelativistisch. Aus
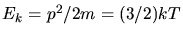 folgt
folgt
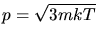 . Daher
. Daher
c) Auch hier nichtrelativistisch. Mit
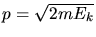 folgt
folgt
d) Die Gesamtenergie ist sehr viel grösser als die Ruheenergie, hier muss relativistisch
gerechnet werden, in diesem Fall kann man die Ruhemasse sogar vernachlässigen.
und daher
e) Die Energie von 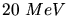 sieht zwar gross aus, ist aber gegenüber der Ruhemasse
des Protons klein. Daher auch hier nichtrelativistisch.
sieht zwar gross aus, ist aber gegenüber der Ruhemasse
des Protons klein. Daher auch hier nichtrelativistisch.
Harm Fesefeldt
2005-05-04