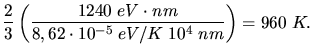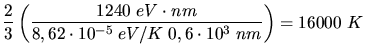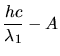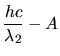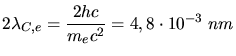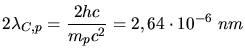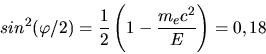Rechenübung am 19/20. April 2005
Vermischte Aufgaben über Photonen, Photoeffekt und Comptoneffekt
Aufgabe 1:
Berechnen Sie die Wellenlänge und den Impuls eines Photons, dessen Energie gleich der
Ruheenergie des Elektrons ist.
Aufgabe 2:
Bei welcher Temperatur wird die mittlere Energie eines Moleküls eines idealen Gases gleich der
mittleren Energie eines Photons der Strahlung
a) des menschlichen Körpers (
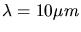 ),
),
b) des sichtbaren Lichtes (
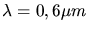 ) ?
) ?
Aufgabe 3:
Eine Metallfläche wird mit Licht der Wellenlänge 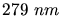 und
und 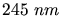 bestrahlt.
Die jeweiligen Bremsspannungen sind
bestrahlt.
Die jeweiligen Bremsspannungen sind 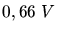 und
und 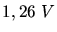 . Berechnen Sie hieraus die
Plancksche Konstante und die Austrittsarbeit des Metalls.
. Berechnen Sie hieraus die
Plancksche Konstante und die Austrittsarbeit des Metalls.
Aufgabe 4:
Vergleichen Sie die maximale Wellenlängenänderung bei der Compton- Streuung von Photonen an freien
Elektronen mit der an Protonen ?
Aufgabe 5:
Ein Photon mit der Energie 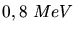 wird an einem freien Elektron gestreut. Die Wellenlänge des gestreuten
Photons ist gleich der Comptonwellenlänge. Unter welchem Winkel wird das Photon gestreut ?
wird an einem freien Elektron gestreut. Die Wellenlänge des gestreuten
Photons ist gleich der Comptonwellenlänge. Unter welchem Winkel wird das Photon gestreut ?
Aufgabe 6:
Bestimmen Sie den Zusammenhang zwischen der Energie des Rückstoßelektrons beim Comptoneffekt
als Funktion des Streuwinkels des Photons.
Lösungen
Aufgabe 1:
Die Energie eines Photons ist
In dieser Aufgabe soll
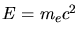 sein, dann ist
sein, dann ist
Den Impuls des Photons rechnen wir mit
Nach Aufgabenstellung sollte wieder
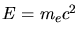 sein, daher
sein, daher
Hier verwendet man üblicherweise die Standardeinheiten mit
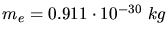 und
und
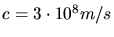 , daher
, daher
Aufgabe 2:
Aus
folgt:
Wir verwenden
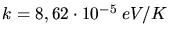 und erhalten
und erhalten
Aufgabe 3:
Aus den Angaben der Aufgabe erhalten wir das Gleichungssystem
mit der Austrittarbeit 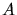 , den Wellenlängen
, den Wellenlängen 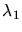 und
und 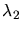 und mit den dazugehörigen
Bremsspannungen
und mit den dazugehörigen
Bremsspannungen 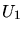 und
und 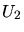 .
.
Berechnung von 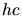 :
:
Berechnung von 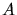 :
:
Aufgabe 4:
Bei der Comptonstreuung am Proton muss man die Componwellenlänge des Protons benutzen:
Die maximale Wellenlängenänderung erhält man für
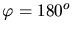 oder
oder
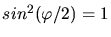 .
Daher
.
Daher
Aufgabe 5:
Wir benutzen die allgemeine Formel
In dieser Aufgabe soll
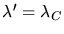 sein, d.h.
sein, d.h.
Mit
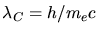 und
und
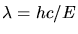 erhalten wir
erhalten wir
und damit
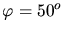 .
.
Aufgabe 6:
Wir schreiben den Energiesatz in der Form
mit der kinetischen Energie 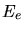 des Rückstosselektrons. Daraus folgt auch
des Rückstosselektrons. Daraus folgt auch
Wir müssen jetzt das 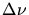 umformen, um einen Ausdruck mit
umformen, um einen Ausdruck mit
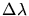 zu
gewinnen:
zu
gewinnen:
Wir schreiben dieses um und erhalten
Eingesetzt in die obige Gleichung und Beachtung von
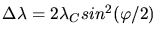 führt auf
führt auf
Das Elektron erhält maximale Energie für
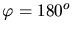 , daher
, daher
Für energiereiche Photonen ist
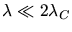 und daher
und daher
Bei hohen Energien geht die Comptonkante in den Photopeak über.
Harm Fesefeldt
2005-04-20