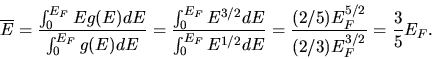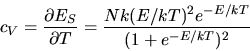Übung Nr.11
Abgabetermin: Montag, d. 11. Juli 2005
Aufgabe 1: (5 Punkte)
a) In der Vorlesung wurde argumentiert, dass bei den Elementen der ersten Gruppe
(Na, K u.s.w.) ein Elektron pro Atom im Leitungsband ist. In dieser Aufgabe wollen wir
uns davon überzeugen, das die angegebenen Formeln der gleiche Ergebnis liefern.
Die Anzahl der Atome pro Volumeneinheit ist für  :
:
Für die weiteren Aufgaben berechnen wir den konstanten Faktor in der Zustandsdichte:
Die Anzahl der Leitungselektronen pro Volumeneinheit ist für niedrige Temperaturen
 :
:
Hierbei haben wir also benutzt, dass 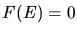 für
für 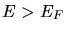 und
und
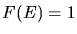 für
für 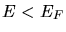 ist. Dann erhalten wir
ist. Dann erhalten wir
Nach dieser Rechnung ist also etwa 1 Leitungselektron pro Atom im Leitungsband.
Diese Zahl sollte weitgehend temperaturunabhängig sein,
da auch bei höheren Temperaturen nur wenige weiteren Elektronen ins Leitungsband
kommen können.
b) Wir bilden das Integral über die Fermi- Verteilung.
Wir approximieren
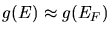 in der Nähe der Fermi- Kante.
Mit
in der Nähe der Fermi- Kante.
Mit
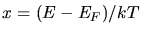 kann das Integral geschrieben werden als
kann das Integral geschrieben werden als
Das sind also 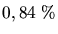 der gesamten Leitungselektronen.
der gesamten Leitungselektronen.
Aufgabe 2: (5 Punkte)
Die Anzahl der Leitungselektronen pro Volumen 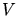 und pro Energieintervall
und pro Energieintervall 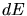 ist
ist
Auch hier approximieren wir wieder 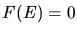 für
für 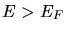 und
und 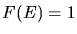 für
für
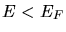 . Dann erhalten wir für den Mittelwert der Energie der Elektronen im Leitungsband:
. Dann erhalten wir für den Mittelwert der Energie der Elektronen im Leitungsband:
Aufgabe 3: (5 Punkte)
Wir bezeichnen die Zustandsdichten der Elektronen mit
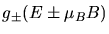 und machen eine Taylor- Entwicklung
und machen eine Taylor- Entwicklung
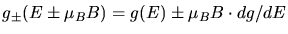 .
Die Magtnetisierung ist dann
.
Die Magtnetisierung ist dann
Der Faktor 1/2 tritt auf, da wir in der ursprünglichen Zustandsdichte wegen der zwei Spinstellungen
einen Faktor 2 haben. Einsetzen der Taylor- Entwicklung ergibt dann
Mit
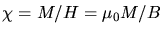 und
und
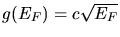 (siehe Aufgabe 1) folgt
(siehe Aufgabe 1) folgt
Kupfer ist natürlich ein ganz schlechtes Beispiel, da es bekanntlich diamagnetisch ist.
Bei Eisen beobachtet man einen Wert von
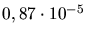 .
.
Aufgabe 4: (5 Punkte)
Am einfachsten verifiziert man die Formel rückwärts. Mit
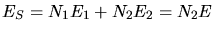 folgt
folgt
oder
Da
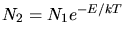 gilt, ist die Formel also richtig.
gilt, ist die Formel also richtig.
b) Die Ableitung der Gesamtenergie nach der Temperatur ergibt
Dieses ist die Schottky- Spez. Wärme und wird bei paramagnetischen Festkörpern bei niedrigen
Temperaturen beobachtet. Die Energiewerte korrespondieren zu der Energieaufspaltung der
magnetischen Momente parallel und antiparallel zum Magnetfeld, siehe Aufgabe 3.
Harm Fesefeldt
2005-07-12
![]() und pro Energieintervall
und pro Energieintervall ![]() ist
ist