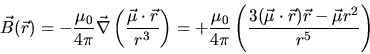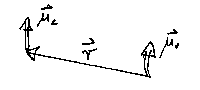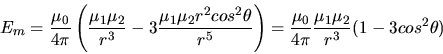Übung Nr.9
Abgabetermin: Montag, d. 27. Juni 2005
Aufgabe 1: (5 Punkte)
a) Die Summe aus der Energieverschiebung durch Spin- Bahn Kopplung,
und der relativistischen Korrektur
soll die gesamte Feinstrukturaufspaltung ergeben. Wir prüfen dieses getrennt für die beiden
Fälle 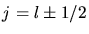 .
.
Sei zunächst 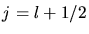 . Dann ist
. Dann ist
Für die Feinstrukturformel folgt dann
Wir ziehen 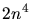 vor die Klammer und bringen die beiden ersten Terme auf einen Hauptnenner:
vor die Klammer und bringen die beiden ersten Terme auf einen Hauptnenner:
Beim zweiten Fall 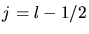 erhalten wir ähnlich
erhalten wir ähnlich
und
b) Wenn der Korrekturm in der FS- Formel verschwinden soll, muß
oder
sein. Da andererseits
so würden wir für den Gesamtdrehimpuls erhalten:
Dieser offensichtliche Widerspruch zeigt, daß unsere angenommene Behauptung nicht möglich ist.
Aufgabe 2: (5 Punkte)
Zunächst müssen die Formeln für das Wasserstoffatom auf die Wasserstoff- ähnlichen
Atome umgeschrieben werden. Dazu muß 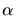 durch
durch 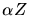 ersetzt werden.
Man sieht dieses sofort, wenn man die Definition von
ersetzt werden.
Man sieht dieses sofort, wenn man die Definition von 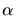 anschreibt:
anschreibt:
das eine 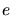 ist die Ladung des Elektrons, das andere
ist die Ladung des Elektrons, das andere 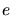 die Ladung des Protons.
Für Kerne mit
die Ladung des Protons.
Für Kerne mit 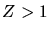 geht dieses über in
geht dieses über in
Die Energieeigenwerte sind dann
und die Feinstruktur- Korrektur
Insgesamt sind unsere Energiewerte also
Mit
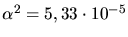 und
und
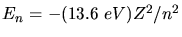 können wir
schreiben
können wir
schreiben
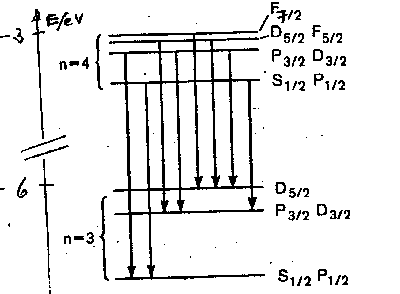
Für 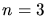 folgt:
folgt:
Entsprechend für 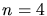 :
:
Skizze:
b) Mit den Auswahlreglen
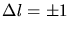 und
und
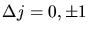 erhält man die
in der obigen Skizze eingezeichneten 8 Übergänge. Da die Feinstrukturformel für jedes
erhält man die
in der obigen Skizze eingezeichneten 8 Übergänge. Da die Feinstrukturformel für jedes
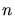 und jedes
und jedes 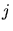 einen anderen Wert liefert, sind die Frequenzen für alle
erlaubten Übergänge verschieden, man erhält also auch 8 verschiedene Spektrallinien.
einen anderen Wert liefert, sind die Frequenzen für alle
erlaubten Übergänge verschieden, man erhält also auch 8 verschiedene Spektrallinien.
Aufgabe 3: (5 Punkte)
a) Das Magnetfeld eines Dipols ist
Die Wechselwirkungsenergie zweier Dipole ist dann
Skizze:
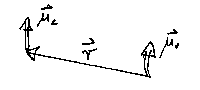
Aus dem Ergebnis
folgt das Maximum bei
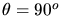 und das Minimum bei
und das Minimum bei
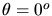 oder
oder 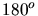 .
.
b) Für das Elektron gilt:
Für das Proton entsprechend mit 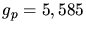 und
und
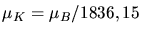 :
:
Die maximale Energie ist
Für das Minimum erhalten wir
Aufgabe 4: (5 Punkte)
Die Korrektur von der Hyperfeinstruktur beträgt
a) Der Abstand aufeinanderfolgender Energieniveaus ist also
b) Es muß einen minimalen Gesamtdrehimpuls geben, diesen nennen wir 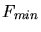 .
Damit erhalten wir mit der Intervallregel das überbestimmte lineare Gleichungssystem:
.
Damit erhalten wir mit der Intervallregel das überbestimmte lineare Gleichungssystem:
mit den Unbekannten 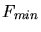 und
und 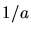 .
. 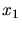 bis
bis 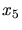 sind die in der Aufgabe angegeben Abstände
zwischen den Niveaus. Mit einem Least Square Fit erhalten wir
sind die in der Aufgabe angegeben Abstände
zwischen den Niveaus. Mit einem Least Square Fit erhalten wir
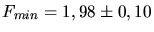 und
und
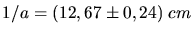 oder
oder
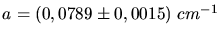 . Daraus folgt der Kerspin
zu
. Daraus folgt der Kerspin
zu
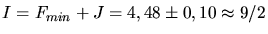 .
.
Harm Fesefeldt
2005-06-30
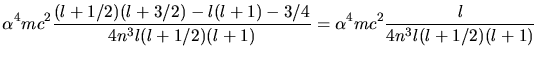
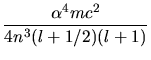
![\begin{displaymath}
E_{n,j} = E_{n} \left[ 1 + \frac{\alpha^{2} Z^{2}}{n^{2}} \left( \frac{n}{j+1/2} - \frac{3}{4}
\right) \right]
\end{displaymath}](img27.gif)
![\begin{displaymath}
E_{n,j} = -(13,6 \; eV) \frac{4}{n^{2}} \left[ 1 + \frac{2,1...
...}}{n^{2}}
\left( \frac{n}{j+1/2} - \frac{3}{4} \right) \right]
\end{displaymath}](img30.gif)

![]() und
und
![]() erhält man die
in der obigen Skizze eingezeichneten 8 Übergänge. Da die Feinstrukturformel für jedes
erhält man die
in der obigen Skizze eingezeichneten 8 Übergänge. Da die Feinstrukturformel für jedes
![]() und jedes
und jedes ![]() einen anderen Wert liefert, sind die Frequenzen für alle
erlaubten Übergänge verschieden, man erhält also auch 8 verschiedene Spektrallinien.
einen anderen Wert liefert, sind die Frequenzen für alle
erlaubten Übergänge verschieden, man erhält also auch 8 verschiedene Spektrallinien.