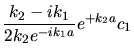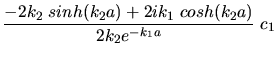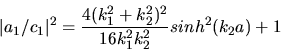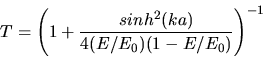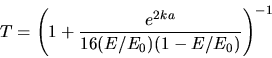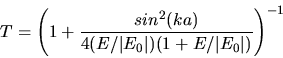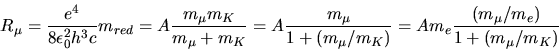Lösungen zur Übung Nr.5
Abgabetermin: Montag, d. 30. Mai 2005
Aufgabe 1: (6 Punkte)
a) Die Schrödinger Gleichung für die drei Bereiche
hat die Lösungen
mit
 und
und
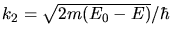 .
Die Durchlasswahrscheinlichkeit ist
.
Die Durchlasswahrscheinlichkeit ist
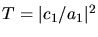 . Gesucht ist also eine Beziehung zwischen
. Gesucht ist also eine Beziehung zwischen
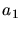 und
und  .
.
Zunächst ist 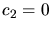 da rechts vom Potentialwall keine nach links laufende
Welle existiert. Aus den Stetigkeitsbedindungen folgt:
da rechts vom Potentialwall keine nach links laufende
Welle existiert. Aus den Stetigkeitsbedindungen folgt:
Wer hier mit allgemeinen Methoden zur Lösung des Geichungssystems anfängt, hat natürlich
verloren. Aus den ersten beiden Bedingungsgleichungen gewinnt man eine Beziehung für
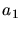 in Anhängigkeit von
in Anhängigkeit von 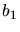 und
und  :
:
Aus den beiden letzten Gleichungen kann man sofort 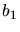 und
und  als Funktion von
als Funktion von
 darstellen:
darstellen:
Einsetzen in die erste Gleichung führt bereits auf die Lösung
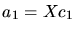 .
Hiermit ist die Aufgabe im Prinzip gelöst und verdient die volle Punktzahl. Alles weitere kann
mit extra Punkten honoriert werden. Am besten schreibt man
.
Hiermit ist die Aufgabe im Prinzip gelöst und verdient die volle Punktzahl. Alles weitere kann
mit extra Punkten honoriert werden. Am besten schreibt man
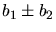 sofort als
Hyperbelfunktionen:
sofort als
Hyperbelfunktionen:
Einsetzen dieser Werte in die obige Gleichung für 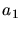 und sortieren nach Real- und
Imaginärteil liefert
und sortieren nach Real- und
Imaginärteil liefert
Bildung des Betragsquadrates und Beachtung von
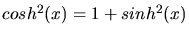 (daher kommt die
einsame 1 in der Formel) liefert
(daher kommt die
einsame 1 in der Formel) liefert
Nach Einsetzen der Werte für 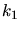 und
und  kann man dieses umschreiben in
kann man dieses umschreiben in
mit
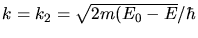 .
.
b) Zunächst ist
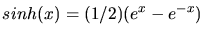 und daher
und daher
Wenn 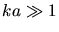 ist, kann der zweite Term gegenüber dem ersten vernachlässigt werden und
wir erhalten
ist, kann der zweite Term gegenüber dem ersten vernachlässigt werden und
wir erhalten
und daher
Bei unser obigen Annahme ist nun aber auch der zweite Term in der Klammer sehr viel grösser
als 1, wir können die 1 in der Klammer vernachlässigen und erhalten
Unsere Annahme ist also
Die Ausdehnung des Potentials muss also sehr viel größer als die Wellenlänge sein.
Aufgabe 2: (5 Punkte)
a) In der Ableitung von Aufgabe ändert sich, daß man  durch
durch 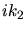 und
und 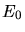 durch
durch 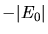 ersetzen
muß, daher (wieder mit
ersetzen
muß, daher (wieder mit  :
:
und
mit
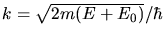 .
.
b) Die Reflektion verschwindet, wenn 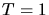 wird, d.h. für
wird, d.h. für 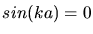 oder
oder  .
Das kann man in Wellenlängen ausdrücken,
.
Das kann man in Wellenlängen ausdrücken,
 oder mit der Energie des Teilchens durch
oder mit der Energie des Teilchens durch
Ähnliches gilt natürlich für den positiven Potentialwall, wenn 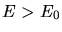 ist.
ist.
Aufgabe 3: (4 Punkte)
Wir erinnern uns an die Formel im Skript:
wobei die Energieabhängigkeit und alle weiteren Konstanten in das  aufgenommen wurden.
Mit
aufgenommen wurden.
Mit
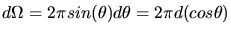 können wir schreiben
können wir schreiben
Das Integral ist dann
mit
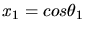 und
und
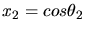 .
Aus der Messung zwischen
.
Aus der Messung zwischen 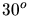 und
und 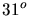 folgt mit
folgt mit 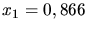 und
und 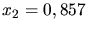 , dass
, dass
a) Den Erwartungswert der Zählrate für Winkel größer als 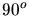 berechnen wir mit
berechnen wir mit
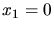 und
und 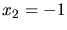 zu
zu
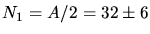 .
.
b) Beim Winkelintervall zwischen 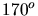 und
und 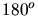 folgt mit
folgt mit
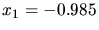 und
und
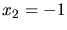 , dass
, dass
 .
Wir erwarten hier also eine Zählrate von entweder
.
Wir erwarten hier also eine Zählrate von entweder 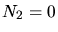 oder
oder 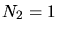 , in seltenen
Fällen auch mehr (Poisson- Verteilung).
, in seltenen
Fällen auch mehr (Poisson- Verteilung).
Aufgabe 4: (5 Punkte)
In unser bisherigen Ableitungen für das Wasserstoffatom muß einfach die Masse
des Elektrons durch die Masse des Muons b.z.w. durch die reduzierte Masse
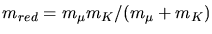 ersetzt werden. Nach Skript ist dann
ersetzt werden. Nach Skript ist dann
Also
Ohne Bewegung des Kerns hätten wir
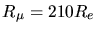 herausbekommen, der Unterschied ist
also nicht vernachlässigbar. Die Ionisierungsenergie ist
herausbekommen, der Unterschied ist
also nicht vernachlässigbar. Die Ionisierungsenergie ist
und die Wellenlänge des Überganges vom ersten angeregten Zustand zum Grundzustand
Harm Fesefeldt
2005-06-01