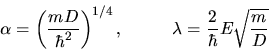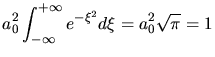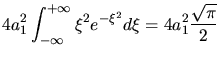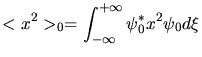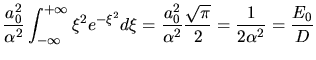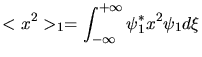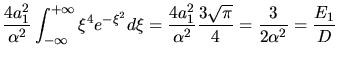Lösungen zur Übung Nr.4
Abgabetermin: Montag, d. 23. Mai 2005
Aufgabe 1: (5 Punkte)
Wir teilen den Spalt in 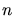 Teile auf, dann können wir für die Teilwelle vom Ort
Teile auf, dann können wir für die Teilwelle vom Ort 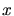 schreiben (siehe Abbildung 1):
schreiben (siehe Abbildung 1):
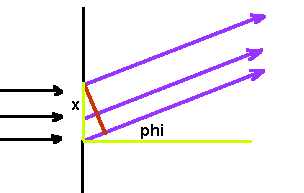
Abbildung 1: Zur Interferenz am Spalt
Berücksichtigt man die Interferenz aller Spaltelemente, so folgt
Das konjugiert Komplexe hiervon ist
Für die Wahrscheinlichkeitsdichte erhalten wir:
Mit
 kann das umgeformt werden auf
kann das umgeformt werden auf
Minima (Nullstellen) erhalten wir für
Für 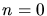 werden Zähler und Nenner Null, der Grenzwert geht bekanntlich gegen
werden Zähler und Nenner Null, der Grenzwert geht bekanntlich gegen 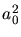 und
ergibt das Hauptmaximum. Der Abstand des ersten Minimums vom Hauptmaximum ist dann
und
ergibt das Hauptmaximum. Der Abstand des ersten Minimums vom Hauptmaximum ist dann
Aufgabe 2: (8 Punkte)
a) Für 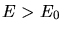 erhalten wir die beiden Gleichungen
erhalten wir die beiden Gleichungen
mit den Lösungen
mit
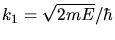 und
und
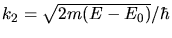 .
Die Randbedingung
.
Die Randbedingung
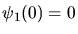 erzwingt
erzwingt 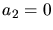 und
und
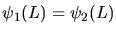 ergibt die Gleichung
ergibt die Gleichung
Aus der dritten Bedingung
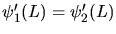 erhalten wir eine zweite Gleichung
erhalten wir eine zweite Gleichung
Weitere Randbedingungen sind nicht vorhanden. Wir haben also lediglich zwei Gleichungen mit 3 Unbekannten
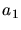 ,
, 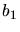 und
und  . Daher ist jeder Wert von
. Daher ist jeder Wert von 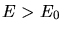 möglich.
möglich.
b) Für 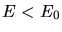 erhalten wir
erhalten wir
mit
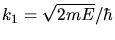 und
und
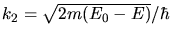 . Die Lösungen sind
. Die Lösungen sind
Wieder muss 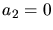 sein. Im Gegensatz zu Teil a) kann man hier sofort
sein. Im Gegensatz zu Teil a) kann man hier sofort  setzen, da
setzen, da
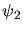 sonst nicht normierbar ist. Wie erhalten also
sonst nicht normierbar ist. Wie erhalten also
Die weiteren Randbedingungen
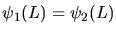 und
und
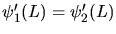 führen auf
führen auf
Hieraus folgt:
Setzen wir 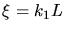 und
und
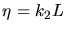 , so ist
, so ist
Das ist offensichtlich die Gleichung eines Kreis mit Radius 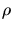 . In einer Skizze mit Achsen
. In einer Skizze mit Achsen  und
und
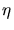 tragen wir die Gleichungen
tragen wir die Gleichungen
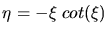 und
und
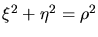 auf.
Da nur Werte
auf.
Da nur Werte 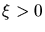 und
und 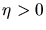 in Frage kommen, erhält man in der Skizze von
Abbildung 2 also lediglich 3 erlaubte Energiewerte.
in Frage kommen, erhält man in der Skizze von
Abbildung 2 also lediglich 3 erlaubte Energiewerte.
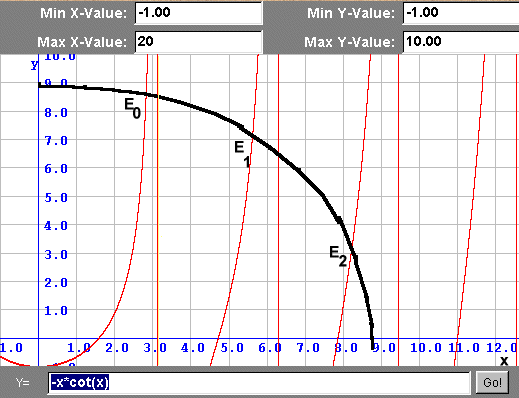
Abbildung 2:
Konstruktionsskizze zur Bestimmung der erlaubten Energiewerte
c) Wenn  wird, gibt es keine Schnittpunkte mehr für
wird, gibt es keine Schnittpunkte mehr für 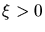 und
und 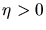 . Damit
überhaupt diskrete Energiewerte auftreten, muß also
. Damit
überhaupt diskrete Energiewerte auftreten, muß also
oder
sein. Aus der Heisenbergschen Unschärferelation können wir eine ähnliche Beziehung
für die Unschärfe der kinetische Energie 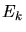 und des Ortes abschätzen
und des Ortes abschätzen
In der Literatur findet man gelegentlich Interpretationsversuche zu dieser Ähnlichkeit,
die mir allerdings nicht besonders einleuchtend erscheinen. Tatsache ist jedoch, das
für 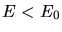 das Maximum der Aufenthaltswahrscheinlichkeit im Potential liegen
müsste, und damit stetige Randbedingungen nicht mehr erfüllt werden können
(siehe Abbildung 3 für den Fall
das Maximum der Aufenthaltswahrscheinlichkeit im Potential liegen
müsste, und damit stetige Randbedingungen nicht mehr erfüllt werden können
(siehe Abbildung 3 für den Fall
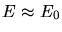 ).
).
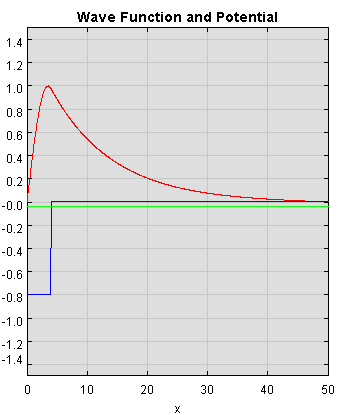
Abbildung 3:
Die erste Wellenfunktion für das minimale Potential
d) Die Aufenthaltswahrscheinlichkeiten sind
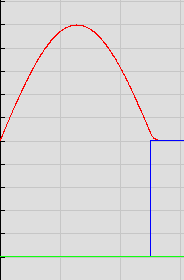
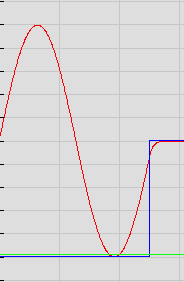

Abbildung 4:
Skizze der ersten drei Wellenfunktionen
Wer hier auch noch die Normierungskonstanten ausrechnet, kriegt einen Extrapunkt.
Aufgabe 3: (7 Punkte)
a) Wir rechnen rückwärts. Mit
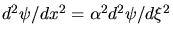 folgt:
folgt:
oder
Vergleich mit
liefert:
Mit
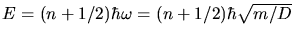 kann man auch schreiben
kann man auch schreiben
b) An der vorherigen Formel sieht man, daß auch  in den Eigenfunktionen vorkommt,
nämlich im Index
in den Eigenfunktionen vorkommt,
nämlich im Index 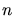 . Die ersten drei Eigenfunktionen sind:
. Die ersten drei Eigenfunktionen sind:
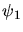 hat keine Nullstelle,
hat keine Nullstelle, 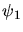 hat eine Nullstelle bei
hat eine Nullstelle bei  ,
,
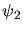 hat 2 Nullstellen bei
hat 2 Nullstellen bei
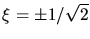 .
.
c) Es ist
da der Integrand eine symmetrisch ungerade Funktion ist.
d) Zur weiteren Berechnung der Erwartungswerte müssen wir zunächst die Normierungen
 und
und 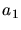 bestimmen. Für die auftretenden bestimmten Integrale verwenden
wir Integraltafeln (siehe z.B. Bronstein - Semendjajew). Wegen
bestimmen. Für die auftretenden bestimmten Integrale verwenden
wir Integraltafeln (siehe z.B. Bronstein - Semendjajew). Wegen
folgt
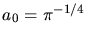 und
und
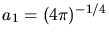 . Die Erwartungswerte sind dann
. Die Erwartungswerte sind dann
Wir erhalten also die klassischen Beziehungen
Man sieht insbesondere noch mal, daß 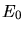 und
und 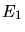 die Gesamtenergien des Teilchens sind,
also Summe aus kinetischer und potentieller Energie.
die Gesamtenergien des Teilchens sind,
also Summe aus kinetischer und potentieller Energie.
Harm Fesefeldt
2005-05-24

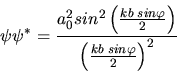
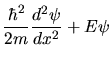
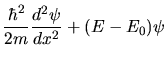

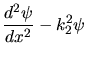

![]() wird, gibt es keine Schnittpunkte mehr für
wird, gibt es keine Schnittpunkte mehr für ![]() und
und ![]() . Damit
überhaupt diskrete Energiewerte auftreten, muß also
. Damit
überhaupt diskrete Energiewerte auftreten, muß also

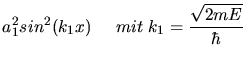
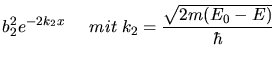



![]() folgt:
folgt: