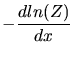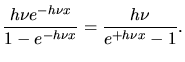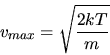Lösungen zur Übung Nr.3
Abgabetermin: Montag, d. 9. Mai 2005
Aufgabe 1
Im allgemeinen findet man in der Literatur Herleitungen über die Wellenzahlen 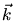 .
Man kann das allerdings auch im normalen Ortsraum herleiten. Im folgenden zeigen wir
eine Kurzform der Herleitung aus dem Buch von Hänsel und Neumann (Spectrum- Verlag).
Wir betrachten einen kantenförmigen Hohlraum mit Kantenlänge
.
Man kann das allerdings auch im normalen Ortsraum herleiten. Im folgenden zeigen wir
eine Kurzform der Herleitung aus dem Buch von Hänsel und Neumann (Spectrum- Verlag).
Wir betrachten einen kantenförmigen Hohlraum mit Kantenlänge 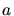 . Die
Bedingung für eine stehende Welle ist:
. Die
Bedingung für eine stehende Welle ist:
wobei 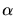 ,
, 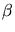 , und
, und 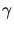 die Richtungswinkel sind. Daraus folgt
die Richtungswinkel sind. Daraus folgt
Wegen
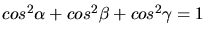 und
und
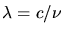 folgt
folgt
Dieses ist die Gleichung einer Kugel mit Radius
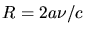 . In der Näherung
grosser Dichten ist die Anzahl der Moden gleich dem Volumen dieser Kugel,
allerdings nur ein Achtel davon, da
. In der Näherung
grosser Dichten ist die Anzahl der Moden gleich dem Volumen dieser Kugel,
allerdings nur ein Achtel davon, da
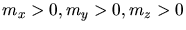 sein sollte.
sein sollte.
Die Modendichte ist dann
Beachtet man noch zwei Polarisationsrichtungen, so folgt endlich
b) Wir setzen 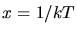 und
und
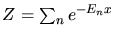 , dann ist
, dann ist
Mit
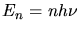 kann man schreiben
kann man schreiben
Der in der Mitte stehende Summe ist nämlich die geometrische Reihe. Wir bilden jetzt
den Logarithmus von 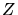 und bilden die Ableitung nach
und bilden die Ableitung nach 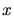 :
:
Also ist
Aufgabe 2:
a) Alle Strahlung, die in eine Fläche 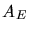 auf der Erde fällt, kommt aus
einer Fäche
auf der Erde fällt, kommt aus
einer Fäche 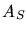 von der Sonnenoberfläche. Aus der Geometrie des Problems
folgt
von der Sonnenoberfläche. Aus der Geometrie des Problems
folgt
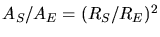 . Hierbei ist
. Hierbei ist 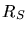 der Radius der
Sonne und
der Radius der
Sonne und 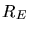 der Abstand der Erde vom Sonnenmittelpunkt. Die Leistungsbilanz ist
der Abstand der Erde vom Sonnenmittelpunkt. Die Leistungsbilanz ist
wobei
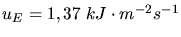 die gemessene Energiestromdichte
auf der Erde ist. Daraus folgt
die gemessene Energiestromdichte
auf der Erde ist. Daraus folgt
Mit
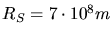 ,
,
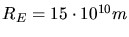 und
und
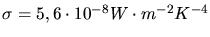 folgt
folgt
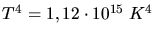 und
und 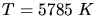 .
.
b) Die gesamte absgestrahlte Energie in der Zeit 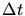 ist
ist
mit der Oberfläche
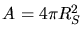 der Sonne. Dann gilt die Energiebilanz
der Sonne. Dann gilt die Energiebilanz
Mit
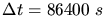 und
und 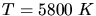 folgt
folgt
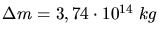 .
Dieses Wert scheint zunächst unheimlich groß zu sein. Fragt man sich allerdings,
in wie vielen Jahren die Masse um
.
Dieses Wert scheint zunächst unheimlich groß zu sein. Fragt man sich allerdings,
in wie vielen Jahren die Masse um 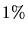 abgenommen hat, so kommt man bei der
Masse der Sonne von
abgenommen hat, so kommt man bei der
Masse der Sonne von
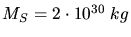 auf den beruhigenden Wert
von etwa
auf den beruhigenden Wert
von etwa 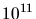 Jahren.
Jahren.
Aufgabe 3:
a) Die Maxwellsche Geschwindigkeitsverteilung ist
Die Transformation auf die Wellenlänge 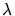 lautet:
lautet:
Den letzten Faktor nennt man auch Jakobi- Determinante.
Wegen
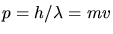 gilt
gilt
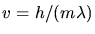 und
und
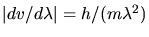 . Einsetzen in die obige Formel führt auf
. Einsetzen in die obige Formel führt auf
b) Das Maximum dieser Verteilung erhält man aus der Bedingung
Nach einer kleinen Rechnung folgt:
Wenn man zunächst den wahrscheinlichsten Wert der Geschwindigkeit berechnet oder die
Jakobi- Determinante vergisst, erhält man
Rechnet man für diesen Wert die de-Broglie Wellenlänge aus, erhält man
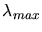 und
und
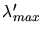 sind offensichtlich nicht identisch, sie unterscheiden sich
voneinander durch einen Faktor
sind offensichtlich nicht identisch, sie unterscheiden sich
voneinander durch einen Faktor 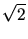 .
.
Aufgabe 4:
a) Bei einer Emissionsdauer von 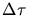 hat das Photon eine Länge von
hat das Photon eine Länge von
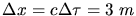 .
.
b) Aus 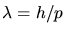 rechnen wir aus, daß
rechnen wir aus, daß
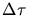 ist offensichtlich die volle Breite in der Unschärfe. Daher
schreiben wir
ist offensichtlich die volle Breite in der Unschärfe. Daher
schreiben wir
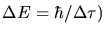 :
:
Nach unser Herleitung ist dieses die halbe Breite (Standardabweichung) der Unschärfe.
Bemerkung: Die Unschärferelationen verbinden Grössen miteinander, die sonst
nicht miteinander verbunden sind. Die Unschärfe (Fehler) abhängiger Grössen
muss natürlich weiterhin mit der normalen Fehlerrechnung behandelt werden.
Zusatzaufgabe in der Übungsstunde (siehe auch Aufgabe 3)
Zeigen Sie, daß die Maxima der spektralen Energiedichten
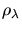 und
und 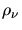 bei verschiedenen Wellenlängen liegen.
bei verschiedenen Wellenlängen liegen.
Lösung
Das Integral über
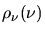 und
und
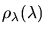 muß gleich sein,
muß gleich sein,
Daraus folgt
und (siehe auch Aufgabe 3)
Wir schreiben die Energiedichte in der Form
Dann gilt
Bedingung für Maximum ist
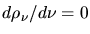 , daraus folgt
, daraus folgt
Setzen wir hier jetzt die Wellenlänge mit
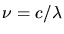 ein so erhalten wir
eine Bestimmungsgleichung für
ein so erhalten wir
eine Bestimmungsgleichung für 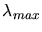 :
:
Die Energiedichte
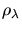 bekommen wir mit
bekommen wir mit
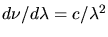 zu
zu
Wir bilden die Ableitung und setzen diese gleich Null:
Dann erhalten wir eine zweite Bestimmungsgleichung für 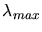 :
:
Diese unterscheidet sich von der ersten Bestimmungsgleichung durch einen Faktor 5
statt einem Faktor 3 vor dem ersten Term. Daher sind die beiden Lösungen
nicht identisch.
Harm Fesefeldt
2005-05-12