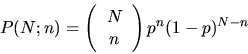Lösungen zur Übung Nr.2
Abgabetermin: Montag, d. 2. Mai 2005
Aufgabe 1
Die Impulsänderung der 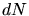 Photonen ist
Photonen ist
wobei 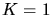 für eine total absorbierende und
für eine total absorbierende und 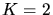 für eine total reflektierende
Fläche ist. Der Druck
für eine total reflektierende
Fläche ist. Der Druck 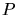 ist
ist
Auf der anderen Seite ist die Intensität durch
gegeben. Eliminieren von 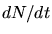 in den letzten beiden Gleichungen
ergibt dann
in den letzten beiden Gleichungen
ergibt dann
Aufgabe 2:
a) Die Änderung der Photonenenergie muss gleich der vom Gravitationsfeld geleisteten
Arbeit sein, daher
Mit
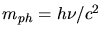 folgt
folgt
Die Integration ergibt
mit dem Radius 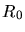 der Sonne und dem Abstand
der Sonne und dem Abstand 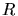 von Sonne und Erde. Da
von Sonne und Erde. Da 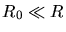 ,
kann man schreiben:
,
kann man schreiben:
Umformen nach der Wellenlänge und Reihenentwicklung ergibt
und daher
Einsetzen der Zahlenwerte,
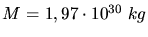 ,
,
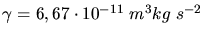 und
und
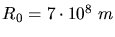 ergibt dann
ergibt dann
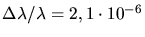 .
.
b) Die Wellenlängenverschiebung verschwindet, wenn der Stern sich mit einer bestimmten
Geschwindigkeit auf uns zubewegt. Dank des Dopplereffektes kann die Wellenlängenänderung
gerade wieder kompensiert werden. Bei der Sonne kann das nicht passieren, aber bei einigen
Sternen kommt das offensichtlich vor.
Aufgabe 3:
Die 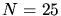 Photonen, die auf die Kathode fallen, sind unabhängig voneinander. Die Wahrscheinlichkeit
für die Erzeugung eines Photoelektrons ist für jedes Photon durch
Photonen, die auf die Kathode fallen, sind unabhängig voneinander. Die Wahrscheinlichkeit
für die Erzeugung eines Photoelektrons ist für jedes Photon durch 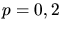 gegeben.
Dann ist die Wahrscheinlichkeit für das Auftreten von
gegeben.
Dann ist die Wahrscheinlichkeit für das Auftreten von 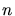 Photoelektronen
durch die Binominalverteilung
Photoelektronen
durch die Binominalverteilung
gegeben. Für kleine Werte von 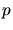 kann man die Poissonsche Näherung
kann man die Poissonsche Näherung
verwenden. In unserer Aufgabe ist diese Näherung allerdings nicht anwendbar.
Da in der Binominalverteilung extrem hohe Potenzen auftreten können, rechnet man am besten
zunächst den Logarithmus von 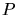 aus:
aus:
und berechnet dann 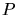 durch die Exponentialfunktion.
Kein Puls wird nach Aufgabenstellung für
durch die Exponentialfunktion.
Kein Puls wird nach Aufgabenstellung für 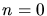 und
und 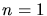 erzeugt, daher
erzeugt, daher
Aufgabe 4:
a) Die allgemeine Formel der Bragg- Reflexion ist
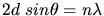 , wobei
, wobei
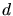 der Abstand der Gitterebenen,
der Abstand der Gitterebenen, 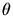 der Glanzwinkel und
der Glanzwinkel und 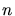 die Ordnung ist.
In erster Ordnung ist also
die Ordnung ist.
In erster Ordnung ist also
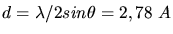 . Diese Lösung entspricht
dem Fall, daß der an der zweiten Ebene reflektierte Strahl um genau ein Wellenlenänge
phasenverschoben ist.
. Diese Lösung entspricht
dem Fall, daß der an der zweiten Ebene reflektierte Strahl um genau ein Wellenlenänge
phasenverschoben ist.
b) Das zweite Maximum bei sonst gleichen Bedingungen wie in a) beobachtet man in der
Simulation bei etwa 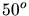 . Dieses ist offensichtlich der Glanzwinkel zweiter Ordnung
(
. Dieses ist offensichtlich der Glanzwinkel zweiter Ordnung
(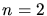 ). Dieser ist
). Dieser ist
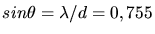 und
und
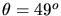 . Weitere
Ordnungen sind in diesem Fall nicht möglich, da z.B. für
. Weitere
Ordnungen sind in diesem Fall nicht möglich, da z.B. für 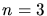 folgt:
folgt:
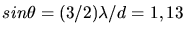 .
.
c) Allgemein ist
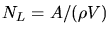 , wobei
, wobei 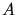 das Atomgewicht und
das Atomgewicht und 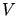 das Volumen
des Moleküls ist. Für
das Volumen
des Moleküls ist. Für 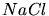 ist
ist
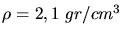 und
und 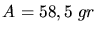 .Rechnet man
mit dem Kugelvolumen
.Rechnet man
mit dem Kugelvolumen
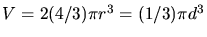 , so erhält man
, so erhält man
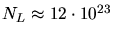 , offensichtlich einen Faktor 2 zu groß. Den richtigen Wert
erhält man mit dem Quadervolumen
, offensichtlich einen Faktor 2 zu groß. Den richtigen Wert
erhält man mit dem Quadervolumen 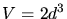 , nämlich
, nämlich
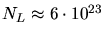 .
.
Harm Fesefeldt
2005-05-04