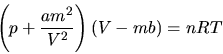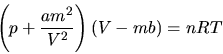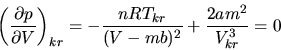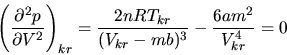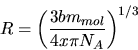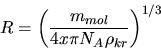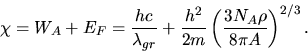Übung Nr.1
Abgabetermin: Montag, d. 25. April 2005
Aufgabe 1: (5 Punkte)
Wir schreiben die van der Waals- Gleichung in der Form
wobei 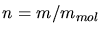 die Anzahl der Mole ist und
die Anzahl der Mole ist und 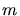 die Masse des Gases bezeichnet. Wir schreiben
die Masse der Gase, um mit
die Masse des Gases bezeichnet. Wir schreiben
die Masse der Gase, um mit
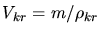 das kritische Volumen durch
das kritische Volumen durch 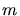 ausdrücken zu
können. Der kritische Punkt ist bekanntlich der Punkt K, indem die Isotherme einen Wendepunkt
mit horizontaler Tangente hat. Wir schreiben
ausdrücken zu
können. Der kritische Punkt ist bekanntlich der Punkt K, indem die Isotherme einen Wendepunkt
mit horizontaler Tangente hat. Wir schreiben 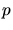 als Funktion von
als Funktion von 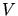 und erhalten
und erhalten
Im kritischen Punkt gilt
Da die Steigung der kritischen Isotherme in K auch noch das Vorzeichen wechselt, muß auch
gelten. Aus den letzten beiden Gleichungen erhält man
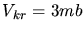 . Mit
. Mit
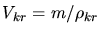 gilt dann
gilt dann
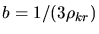 . Das Korrekturglied
. Das Korrekturglied 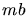 in der Gleichung ist das kleinste Volumen, daß das Gas
einnehmen kann. Es ist ein gewisses Vielfaches des Eigenvolumens,
in der Gleichung ist das kleinste Volumen, daß das Gas
einnehmen kann. Es ist ein gewisses Vielfaches des Eigenvolumens,
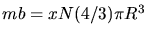 mit
der Anzahl der Moleküle
mit
der Anzahl der Moleküle 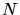 . Die beste Beschreibung erhält man mit
. Die beste Beschreibung erhält man mit 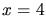 .
Wir lassen den Faktor aber zunächst offen. Verwendet man
.
Wir lassen den Faktor aber zunächst offen. Verwendet man
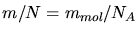 , so folgt
, so folgt
und damit
Mit
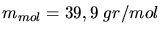 und
und
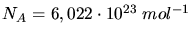 folgt
folgt
Mit der Annahme 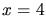 erhält man als Abschätzung:
erhält man als Abschätzung:
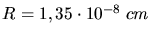 .
.
Aufgabe 2: (5 Punkte)
Dieses ist eine Literatur- Research Aufgabe und steht in jedem besseren Buch.
Eine schöne Seite findet man im Internet
hier,
ein sehr schönes Java- Applet auf
dieser Seite
Aufgabe 3: (5 Punkte)
Wie in der Festkörperphysik üblich, legen wir den Nullpunkt der Energieskala auf den
Boden des Potentials (Anfang des Leitungsbandes). Dann ist das Potential bis zur kinetischen
Energie 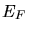 mit Elektronen aufgefüllt. Mit
mit Elektronen aufgefüllt. Mit 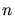 in der Formel für
in der Formel für
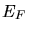 sind natürlich nur die Leitungselektronen gemeint, da die fest gebundenen
Elektronen in diesem Problem keine Rolle spielen.
Mit
sind natürlich nur die Leitungselektronen gemeint, da die fest gebundenen
Elektronen in diesem Problem keine Rolle spielen.
Mit
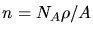 und der Austrittsarbeit
und der Austrittsarbeit 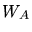 folgt
folgt
Mit
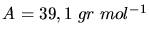 und
und
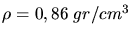 folgt:
folgt:
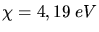 .
.
Aufgabe 4: (5 Punkte)
Die maximale Energie 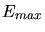 erhält das Elektron bei der Rückwärtsstreuung des Photons,
also für
erhält das Elektron bei der Rückwärtsstreuung des Photons,
also für
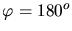 . Der Energiesatz für diesen speziellen Fall können wir schreiben als
. Der Energiesatz für diesen speziellen Fall können wir schreiben als
Also gilt:
und
Die Energie des Photoelektrons ist
und die Maximalenergie der Rückstoßelektronen:
Ein Java Applet,
daß solche Energiespektren simuliert, hat Torsten Franke in seiner
Staatsexamensarbeit für das höhere Lehramt geschrieben. Nach dem Starten des Programms
erscheint der experimentelle Aufbau. Von links nach rechts ist zunächst eine radioaktive
Quelle, dann ein Kollimator zur Begrenzung des Photonenstrahls, gefolgt von einem
Scintillationszähler. In diesem Material finden die Wechselwirkungen des Photons statt.
Alternativ können Photoeffekt oder Comptoneffekt auftreten. Da der Zähler relativ groß ist,
kann das gestreute Photon beim Comptoneffekt weitere Wechselwirkungen machen. Die erzeugten Elektronen
werden abgebremst, wobei Scintillationslicht im sichtbaren Bereich entsteht. Dieses Licht
wird durch Reflektionen auf einen ganz rechts angebrachten Photomultiplier gelenkt (im Applet
nicht zu erkennen). Es entsteht
also ein Puls, der der Energie der abgebremsten Elektronen proportional ist. Links oben im
Applet- Fenster ist noch eine Lupe angebracht, mit der man die Wechselwirkung im Zoom betrachten
kann. In einem weiteren aufklappbaren Fenster (VKA) werden die Energiespektren
in einem Vielkanal- Analysator gezeigt. Den experimentellen Aufbau kann man im Fenster Aufbau
verändern. Im Fenster Prozeßdaten werden Sie feststellen, daß die Elektronen noch weitere
Prozesse mit der Materie des Scintillationszählers machen können. Die letzten beiden Menuepunkte
ganz rechts (Totale WQ, Diff. WQ) dienen zur Darstellung der Wahrscheinlichten der
Wechselwirkungen. Wir haben in der Vorlesung bis jetzt nur die reine Kinematik der Prozesse
gelernt (Energie- und Impulserhaltung). Die Frage nach der Wahrscheinlichkeit zum Beispiel,
mit der ein Photon unter einem bestimmten Winkel 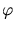 gestreut wird,
kann erst in der Quantenelektrodynamik und Teilchenphysik beantwortet werden.
gestreut wird,
kann erst in der Quantenelektrodynamik und Teilchenphysik beantwortet werden.
Harm Fesefeldt
2005-04-26