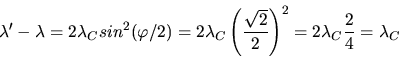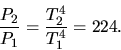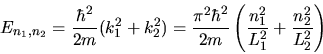Lösungen zur Klausur zur Physik IV, SS 2005
Abgabetermin: Samstag, d. 16. Juli 2005, 11:30
Aufgabe 1: (10 Punkte)
Wir rechnen zunächst die Energie des Rückstoß- Elektrons aus. Der Energiesatz lautet
Aus der Formel für die Compton- Streuung erhalten wir
Die Energie der Elektronen ist dann
Wir müssen also relativistisch weiterrechnen. Aus
folgt
und daher
Aufgabe 2: (6 Punkte)
a) Mit dem Stefan- Boltzmann Gesetz
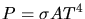 folgt bei gleicher Oberfläche
folgt bei gleicher Oberfläche 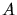 :
:
b) Das Wiensche Verschiebungsgesetz sagt uns, daß
c) Die Wellenlänge mit dem maximalen Energiebeitrag wird also kleiner.
Aufgabe 3: (10 Punkte)
a) Die stationäre Schrödingergleichung lautet für diesen Fall
Wir legen das Potential 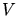 so, daß
so, daß 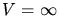 für
für 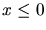 ,
, 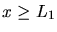 und
und 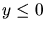 ,
,
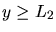 .
Lösungen mit
.
Lösungen mit 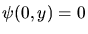 und
und 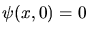 sind dann
sind dann
Aus den Randbedingungen
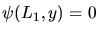 für
für 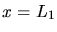 und
und
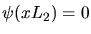 für
für 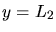 folgt
folgt
Wir setzen die Wellenfunktion mit den zweiten Ableitungen in die Schrödingergleichung ein und erhalten
Daraus folgen die Energiewerte
b) Der einfachste Fall für entartete Energiewerte ist
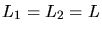 . In diesem Fall gilt
. In diesem Fall gilt
Jedes Vertauschen der Quantenzahlen liefert dann den gleichen Energiewert.
Aufgabe 4: (10 Punkte)
Der Gesamtdrehimpuls spaltet in 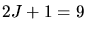 Zustände auf. Daher ist
Zustände auf. Daher ist 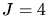 . Aus dem Termsymbol
entnehmen wir, daß
. Aus dem Termsymbol
entnehmen wir, daß 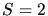 und
und 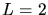 . Der Lande- Faktor des Atoms ist also
. Der Lande- Faktor des Atoms ist also
Die maximale Komponente des magnetichen Momentes in Feldrichtung ist also
Aufgabe 5: (8 Punkte)
a) Das magnetische Moment des Protons ist
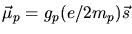 mit der
mit der 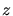 - Komponente
- Komponente
Das obere Vorzeichen korrespondiert also immer zum Fall, daß der Spin parallel zum Magnetfeld
steht. Die magnetische Wechselwirkungsenergie ist
Der Abstand beider Niveaus ist daher
und das Verhältnis der Besetzungszahlen
oder
b) Wie aus obiger Formel für 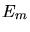 ersichtlich, ist der Zustand mit Spin parallel zum Feld
der Zustand mit der kleineren Energie (negativ). Dieser hat also die höhere Besetzungszahl.
ersichtlich, ist der Zustand mit Spin parallel zum Feld
der Zustand mit der kleineren Energie (negativ). Dieser hat also die höhere Besetzungszahl.
Aufgabe 6: (6 Punkte)
Die 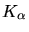 - Linie hat zwar eine Energie von
- Linie hat zwar eine Energie von
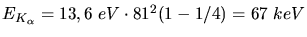 . Das nützt uns aber nicht viel, da wir den Platz auf der
. Das nützt uns aber nicht viel, da wir den Platz auf der 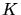 - Schale erst mal
frei machen müssen. Dazu benötigen wir die Energie
- Schale erst mal
frei machen müssen. Dazu benötigen wir die Energie
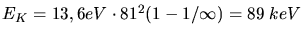 . Unsere Energie von
. Unsere Energie von 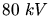 reicht
also nicht aus.
reicht
also nicht aus.
Harm Fesefeldt
2005-07-16