




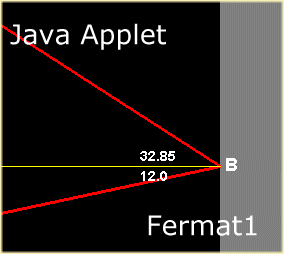
 Ein Lichtstrahl soll von Punkt A ausgehend an einem Spiegel reflektiert werden und dann nach
Punkt P laufen. Welchen Weg nimmt der Lichtstrahl ? Nun, unser Licht ist schlau und wählt
natürlich den kürzesten Weg. Suchen Sie diesen kürzesten Weg in unserem ersten
Applet. Den Einfallswinkel
Ein Lichtstrahl soll von Punkt A ausgehend an einem Spiegel reflektiert werden und dann nach
Punkt P laufen. Welchen Weg nimmt der Lichtstrahl ? Nun, unser Licht ist schlau und wählt
natürlich den kürzesten Weg. Suchen Sie diesen kürzesten Weg in unserem ersten
Applet. Den Einfallswinkel 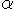 des Lichtes auf den Spiegel können Sie
variieren, das Programm berechnet den Lichtweg Lopt und zeigt den Wert an. Sie werden
bemerken, dass beim kleinsten Lichtweg gerade der Reflexionswinkel
des Lichtes auf den Spiegel können Sie
variieren, das Programm berechnet den Lichtweg Lopt und zeigt den Wert an. Sie werden
bemerken, dass beim kleinsten Lichtweg gerade der Reflexionswinkel 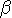 gleich dem Einfallswinkel
gleich dem Einfallswinkel  ist. Bei der Reflexion und Brechung gibt
man grundsätzlich die Winkel mit der Normalen der Begrenzungsflächen an. Sie können
sich die Sucherei ersparen, indem Sie auf den Button Search klicken. Dann sucht das
Programm den kürzesten Lichtweg.
ist. Bei der Reflexion und Brechung gibt
man grundsätzlich die Winkel mit der Normalen der Begrenzungsflächen an. Sie können
sich die Sucherei ersparen, indem Sie auf den Button Search klicken. Dann sucht das
Programm den kürzesten Lichtweg. Die Bedienung dieses ersten Applets, sowie auch aller weiteren, ist folgendermassen: Nach dem Laden des Programms erscheint zunächst eine Bezier- Animation der experimentellen Anordnung. Mit Stop und Start können Sie diese Animation starten und stoppen, mit Reset wird das eigentliche Applet gestartet. Achten Sie darauf, dass das separate Control- Fenster nicht vom Browser oder vom Applet verdeckt wird. Bei fast allen Applets können die Parameter mit Auswahlfeldern verändert werden. Die Änderung wird in einigen Applets sofort übernommen, in anderen dagegen erst bei erneutem Drücken des Reset Buttons.
Aufgabe 1: Zeigen Sie mit einer analytischen Rechnung, dass der Weg des Lichtstrahls zwischen zwei festen Punkten A und P bei der Reflektion an einem ebenen Spiegel minimal ist, wenn der Einfallswinkel gleich dem Ausfallswinkel ist.
 Bei der Brechung des Lichtstrahls an einer ebenen Begrenzungsfläche zweier Medien überlegt
sich der Lichtstrahl eine kleine Änderung seines Vorgehens. Er wählt nicht den
kürzesten Weg, sondern den schnellsten Weg. Seine Geschwindigkeit im Medium 1 ist c/n1,
im Medium 2 dagegen c/n2. Hierbei sind n1 und n2 die Brechungsindizes
der Medien und c die Lichtgeschwindigkeit im Vakuum. Da er die Strecke s1 in der Zeit
Bei der Brechung des Lichtstrahls an einer ebenen Begrenzungsfläche zweier Medien überlegt
sich der Lichtstrahl eine kleine Änderung seines Vorgehens. Er wählt nicht den
kürzesten Weg, sondern den schnellsten Weg. Seine Geschwindigkeit im Medium 1 ist c/n1,
im Medium 2 dagegen c/n2. Hierbei sind n1 und n2 die Brechungsindizes
der Medien und c die Lichtgeschwindigkeit im Vakuum. Da er die Strecke s1 in der Zeit
t1 = s1 n1/c
und die Strecke s2 in der Zeit
t2 = s2 n2/c
zurücklegt, ist die Gesamtzeit
t = t1 + t2 = (s1 n1 + s2 n2)/c.
Man kann also auch sagen, dass das Licht den Weg mit der kürzesten optischen Weglänge
Lopt = s1 n1 + s2 n2
wählt. In unserem zweiten Applet können Sie diese kürzeste optische Weglänge suchen. Wiederum nimmt Ihnen das Applet die Sucherei ab, wenn Sie auf Search klicken. Unser virtuelles Experiment zeigt, dass bei der kleinsten optischen Weglänge gerade
n1 sin( ) = n2 sin(
) = n2 sin(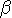 )
)
gilt, wenn 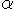 und
und 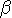 die Einfalls- und
Ausfallswinkel sind. Im Applet haben wir n1 = 1 und n2 = n gesetzt.
Der Brechungsindex n kann verändert werden.
Dieses ist aber nichts anderes als das Ihnen sicherlich bekannte Snell'sche Brechungsgesetz.
die Einfalls- und
Ausfallswinkel sind. Im Applet haben wir n1 = 1 und n2 = n gesetzt.
Der Brechungsindex n kann verändert werden.
Dieses ist aber nichts anderes als das Ihnen sicherlich bekannte Snell'sche Brechungsgesetz.
Aufgabe 2 Zeigen Sie mit einer analytischen Rechnung, dass bei der Brechung an einer
ebenen Begrenzungsfläche zweier Medien mit Brechungsindex n1 und n2
der optische Weg zwischen zwei Punkten A und P minimal ist, wenn das Snell'sche Brechungsgesetz
gilt.
Was wir im ersten und zweiten Applet benutzt haben, ist das Prinzip von Fermat:
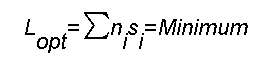
Bei einer kontnuierlichen Veränderung des Brechungsindex kann die Summe als Integral geschrieben werden:
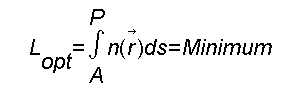
 Bei einer Brechung an einer Begrenzung zwischen zwei Medien wird grundsätzlich auch ein Teil R
der Intensität reflektiert. Aus den Fresnel'schen Formeln erhalten wir
näherungsweise
Bei einer Brechung an einer Begrenzung zwischen zwei Medien wird grundsätzlich auch ein Teil R
der Intensität reflektiert. Aus den Fresnel'schen Formeln erhalten wir
näherungsweise
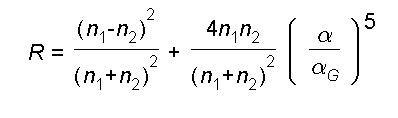
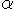 ist wieder der Einfallswinkel,
ist wieder der Einfallswinkel, 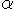 G
der Grenzwinkel. Wenn n1 < n2, dann ist
G
der Grenzwinkel. Wenn n1 < n2, dann ist
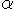 G = 90o. Die Intensität des einfallenden
Lichtstrahls ist in der Formel auf 1 normiert. Daher ist die Intensität des gebrochenen
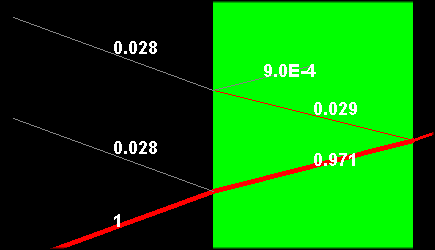
Strahls T = 1 - R. Bei kleinen Einfallswinkeln ist der Anteil der Reflektion im Bereich
von einigen Prozenten, bei grossen Einfallswinkeln steigt er auf 100 Prozent an.
G = 90o. Die Intensität des einfallenden
Lichtstrahls ist in der Formel auf 1 normiert. Daher ist die Intensität des gebrochenen
Strahls T = 1 - R. Bei kleinen Einfallswinkeln ist der Anteil der Reflektion im Bereich
von einigen Prozenten, bei grossen Einfallswinkeln steigt er auf 100 Prozent an.
In unserem Applet können Sie wiederum den Einfallswinkel einstellen und die Intensität
der reflektierten und gebrochenen Strahlen ablesen. Auch hier ist wieder n1 = 1 und
n2 = n gesetzt. Man beobachtet weiterhin, dass nach der zweiten Brechung vom dichteren
Medium zur Luft der Strahl wieder exakt parallel zum ursprünglichen Strahl ist, er ist
lediglich versetzt. Bei dieser Brechung vom optisch dichteren Medium 2 zum dünneren Medium 1
kann eine weitere Komplikation auftreten, nämlich dass sin(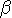 ) = 1
und damit
) = 1
und damit 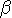 = 90o wird. Dann gilt
= 90o wird. Dann gilt
sin(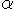 G) = n1/n2
G) = n1/n2
Dieser Winkel  G heisst Grenzwinkel. Für grössere
Einfallswinkel gibt es keinen gebrochenen Strahl mehr, wir haben es mit Totalreflektion zu tun.
Die folgende Abbildung zeigt den oben angegebenen Reflexionskoeffizienten R.
G heisst Grenzwinkel. Für grössere
Einfallswinkel gibt es keinen gebrochenen Strahl mehr, wir haben es mit Totalreflektion zu tun.
Die folgende Abbildung zeigt den oben angegebenen Reflexionskoeffizienten R.
Der Brechnungsindex für Luft an der Erdoberfläche beträgt 1.0003, optische
Gläser haben Werte zwischen 1.4 und 2, der Diamant hat mit 2.42 einen der grössten
Brechungsindizes aller Materialien.
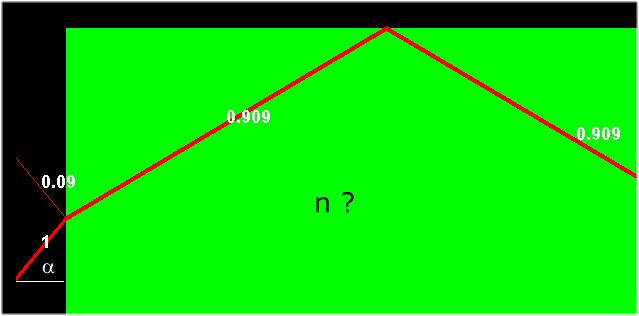
Aufgabe 3: Licht tritt aus der Luft in einen rechteckigen Block eines unbekannten
Materials. Bei einem Einfallswinkel von  < 56o beobachtet
man Totalreflektion des gebrochenen Strahls an der horizontalen Begrenzung (siehe Bild).
Wie gross ist der Brechungsindex des Materials ?
< 56o beobachtet
man Totalreflektion des gebrochenen Strahls an der horizontalen Begrenzung (siehe Bild).
Wie gross ist der Brechungsindex des Materials ?
(Dieses Applet kann Ihnen bei der Lösung helfen).
 Aufgabe 4: Ein Lichtstrahl durchdringt nacheinander k vertikal angeordnete Glasplatten
mit verschiedenen Brechungsindizes. Zeigen Sie rechnerisch, dass der letzte wieder
in Luft austretende Strahl gegenüber dem einfallenden Strahl nur parallel
verschoben ist. (siehe Applet Brechung1)
Aufgabe 4: Ein Lichtstrahl durchdringt nacheinander k vertikal angeordnete Glasplatten
mit verschiedenen Brechungsindizes. Zeigen Sie rechnerisch, dass der letzte wieder
in Luft austretende Strahl gegenüber dem einfallenden Strahl nur parallel
verschoben ist. (siehe Applet Brechung1)
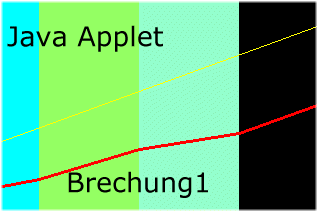
 Will man die Richtung des Lichtstrahles ändern, muss man die Glasplatten horizontal
anordnen. Im Applet Brechung2 haben wir 10 Platten mit linear kleiner werdenden
Brechungsindizes von 1.5 bis 1.05 angeordnet. Die Schwärzung ist ein visuelles
Maass für den Brechungsindex.
Will man die Richtung des Lichtstrahles ändern, muss man die Glasplatten horizontal
anordnen. Im Applet Brechung2 haben wir 10 Platten mit linear kleiner werdenden
Brechungsindizes von 1.5 bis 1.05 angeordnet. Die Schwärzung ist ein visuelles
Maass für den Brechungsindex.
 ist hier nicht der Einfallswinkel, sondern der Ausfallswinkel bei
Eintritt in die erste Glasschicht. Man beobachtet für einen Winkel
von 40o eine fast kreisförmige Bahn, bei 30o tritt der Lichtstrahl
fast parallel zur optischen Achse aus, bei 25o wird der Strahl sogar
an einer Schicht total reflektiert und ändert das Vorzeichen der Steigung.
Die bei jeder Brechung auftretenden normal reflektierten Strahlen wurden vernachlässigt.
In späteren Applets werden wir diese Anordung verfeinern und zu kontinuierlichen
Veränderungen des Brechungsindex übergehen. Dabei werden wir einige interessante
Entdeckungen machen.
ist hier nicht der Einfallswinkel, sondern der Ausfallswinkel bei
Eintritt in die erste Glasschicht. Man beobachtet für einen Winkel
von 40o eine fast kreisförmige Bahn, bei 30o tritt der Lichtstrahl
fast parallel zur optischen Achse aus, bei 25o wird der Strahl sogar
an einer Schicht total reflektiert und ändert das Vorzeichen der Steigung.
Die bei jeder Brechung auftretenden normal reflektierten Strahlen wurden vernachlässigt.
In späteren Applets werden wir diese Anordung verfeinern und zu kontinuierlichen
Veränderungen des Brechungsindex übergehen. Dabei werden wir einige interessante
Entdeckungen machen.
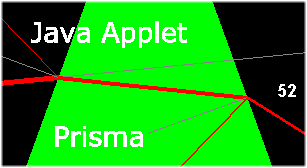 Besonders wichtig in optischen Anwendungen ist das Prisma. Es besteht aus einem
gleichschenkligen Dreieck, den oberen Dreieckswinkel nennt man den
brechenden Winkel. Wir bezeichnen ihn mit
Besonders wichtig in optischen Anwendungen ist das Prisma. Es besteht aus einem
gleichschenkligen Dreieck, den oberen Dreieckswinkel nennt man den
brechenden Winkel. Wir bezeichnen ihn mit 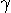 . Das Licht wird zweimal
gebrochen. Die Gesamtablenkung
. Das Licht wird zweimal
gebrochen. Die Gesamtablenkung 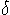 ist abhängig vom ersten
Einfallswinkel
ist abhängig vom ersten
Einfallswinkel 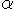 1 und dem brechenden Winkel. Aus der
Geometrie folgt
1 und dem brechenden Winkel. Aus der
Geometrie folgt
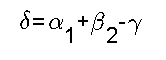
Für rechnerische Zwecke benötigt man weiterhin die Tatsache, dass
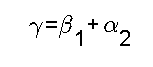
gilt. Bei symmetrischem Strahlengang, also
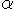 1=
1=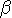 2 und
2 und
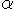 2=
2=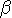 1,
verläuft der Strahl parallel zur Grundfläche, die Gesamtablenkung
erreicht dann ein Minimum. Mit dieser Einstellung wird häufig der Brechungsindex
gemessen:
1,
verläuft der Strahl parallel zur Grundfläche, die Gesamtablenkung
erreicht dann ein Minimum. Mit dieser Einstellung wird häufig der Brechungsindex
gemessen:
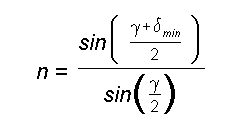
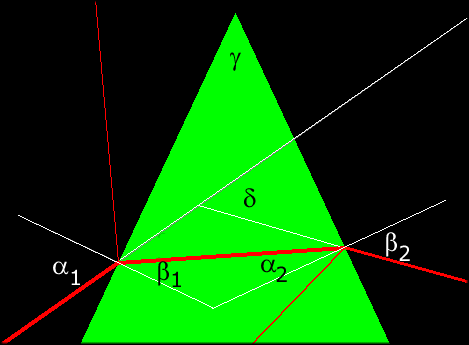
Den brechenden Winkel und den Einfallswinkel können Sie in unserem Applet
verändern. Weiterhin ist rechts der Ausfallswinkel 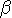 2
angegeben.
Der Brechungsindex ist fest und beträgt n=1.8 (Flintglas).
2
angegeben.
Der Brechungsindex ist fest und beträgt n=1.8 (Flintglas).
Eine weitere wichtige Anwendung ist die Messung der Dispersion. Wir haben in allen
bisherigen Applets monochromatisches Licht angenommen, d.h. unser Lichtstrahl besteht nur aus
Licht einer einzigen Wellenlänge, z.B. rotes Licht.
Normales Tageslicht oder das Licht bestimmter
Lichtquellen besteht aber immer aus einer Mischung von mehreren Wellenlängen.
Der Brechungsindex ist aber abhängig von der Wellenlänge. Diese Abhängigkeit
nennt man Dispersion. Man bekommt dann eine Aufspaltung des gebrochenen Lichtes in die
verschiedenen Farben, aus denen das einfallende Licht besteht. Im Applet haben wir
den Button Dispersion on/off eingebaut, mit dem Sie die Dispersion ein- und
ausschalten können. Wir haben eine Lichtquelle mit sämtlichen Farben des
sichtbaren Spektrums angenommen. Der Brechungsindex variiert zwischen 1.75 und 1.85.
In allen folgenden Applets werden wir diese Dispersion ignorieren und monchromatisches
Licht verwenden.
Aufgabe 5: In der Literatur findet man häufig die einfache Formel
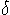 =(n - 1)
=(n - 1)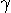 für die Gesamtablenkung
des Prismas. Unter welchen Vorraussetzungen gilt diese Formel ?
für die Gesamtablenkung
des Prismas. Unter welchen Vorraussetzungen gilt diese Formel ?
In allen bisherigen Applets haben wir Reflektion und Brechung an ebenen Flächen
betrachtet. Wir gehen jetzt über zu kugelflächigen Spiegeln und Brechungsebenen.
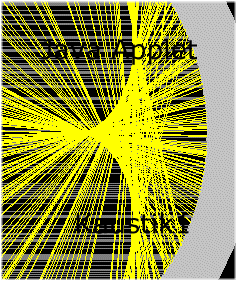
Im Applet Kaustik1 haben wir einen kugelförmigen Hohlspiegel programmiert. Die Symmetrieachse
des Spiegels nennt man die optische Achse. Wir betrachten parallel zur optischen Achse
einlaufende Lichtstrahlen. Der Einfallswinkel ist jetzt der Winkel zwischen dem
Lichtstrahl und der Normalen auf die Ebene, in diesem Fall der Radiusvektor der Kugel.
Beim Spiegel ist der Ausfallswinkel gleich dem Einfallswinkel. Der reflektierte Strahl
schneidet die optische Achse in einem Punkt P. Man beobachtet, dass dieser Schnittpunkt
vom Abstand des einfallenden Strahls von der optischen Achse abhängt.
Wenn man in den Rechnungen sin(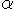 ) =
) = 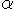 = tan(
= tan(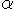 )
setzt, erhält man einen wohldefinierten Brennpunkt bei einem Abstand f = R/2
vom Spiegel. Diesen Punkt haben wir im Applet mit F bezeichnet. Diese Näherung gilt
ersichtlich nur für achsennahe Strahlen, bei denen der Einfallswinkel klein ist.
Der Abstand kann im Applet verändert werden. Mit dem Button Random kann man
gleichzeitig 200 Strahlen mit zufälligen Abständen von der optischen Achse erzeugen.
Das dabei entstehende merkwürdige Bild der reflektierten Strahlen nennt man auch
die Kaustik.
)
setzt, erhält man einen wohldefinierten Brennpunkt bei einem Abstand f = R/2
vom Spiegel. Diesen Punkt haben wir im Applet mit F bezeichnet. Diese Näherung gilt
ersichtlich nur für achsennahe Strahlen, bei denen der Einfallswinkel klein ist.
Der Abstand kann im Applet verändert werden. Mit dem Button Random kann man
gleichzeitig 200 Strahlen mit zufälligen Abständen von der optischen Achse erzeugen.
Das dabei entstehende merkwürdige Bild der reflektierten Strahlen nennt man auch
die Kaustik.
Auch bei einer Brechung an einer Kugelfläche (Kaustik2) beobachtet man, dass
der Schnittpunkt der gebrochenen Strahlen mit der optischen Achse vom Abstand des
einfallenden Strahls von der optischen Achse abhängt. Für achsennahe Strahlen ergibt hier
die Rechnung einen definierten Brennpunkt im Abstand f=n2R/(n2-n1)
von der brechenden Kugelfläche. Auch hier sieht man, dass nur achsennahe Strahlen durch den
Brennpunkt laufen.

 In den beiden folgenden Applets Brennpunkt1 und Brennpunkt2 haben wir die Geometrie
der Flächen geringfügig verändert. Aus dem Hohlspiegel wird ein parabolischer
Spiegel und aus der brechenden Kugelfläche wird ein Ellipsoid. Hier beobachten wir jetzt,
dass für alle parallel einlaufende Strahlen die reflektierten b.z.w. gebrochenen Strahlen
die optische Achse in exakt dem gleichen Punkt schneiden. Bei der Ellipse ist dieses der rechte
Brennpunkt der Ellipse. Solche Spiegel und Flächen sind natürlich technisch
schwierig herzustellen. Daher verwendet man in der Praxis meistens kugelförmige
Flächen und beschränkt sich auf achsennahe Strahlen. Das nennt man dann
paraxiale Optik.
In den beiden folgenden Applets Brennpunkt1 und Brennpunkt2 haben wir die Geometrie
der Flächen geringfügig verändert. Aus dem Hohlspiegel wird ein parabolischer
Spiegel und aus der brechenden Kugelfläche wird ein Ellipsoid. Hier beobachten wir jetzt,
dass für alle parallel einlaufende Strahlen die reflektierten b.z.w. gebrochenen Strahlen
die optische Achse in exakt dem gleichen Punkt schneiden. Bei der Ellipse ist dieses der rechte
Brennpunkt der Ellipse. Solche Spiegel und Flächen sind natürlich technisch
schwierig herzustellen. Daher verwendet man in der Praxis meistens kugelförmige
Flächen und beschränkt sich auf achsennahe Strahlen. Das nennt man dann
paraxiale Optik.
Aufgabe 6:Zeigen Sie mit Hilfe des Fermat'schen Prinzips, dass bei einem parabolischen
Hohlspiegel für alle parallel einfallenden Strahlen die reflektierten Strahlen
die optische Achse in ein und demselben Punkt schneiden. Denken Sie hierbei an die
eigentliche Definition einer Parabel. Ausserdem müssen Sie annehmen, dass alle
parallel einfallenden Strahlen von derselben Lichtquelle kommen und bis dahin gleiche
optische Weglängen durchlaufen haben.
 Linsen bestehen aus Glas, Kunststoff oder anderen durchsichtigen Materialien. Bei sphärischen
Linsen sind die Begrenzungsflächen Teile von Kugelflächen. Lichtstrahlen, die durch
die Linse hindurchtreten, werden zweimal gebrochen. Bei der Konstruktion von Strahlengängen
fasst man beide Brechungen zu einer in der Hauptebene erfolgenden Brechung zusammen. Alle
Abstände sind auf diese Hauptebene bezogen.
Linsen bestehen aus Glas, Kunststoff oder anderen durchsichtigen Materialien. Bei sphärischen
Linsen sind die Begrenzungsflächen Teile von Kugelflächen. Lichtstrahlen, die durch
die Linse hindurchtreten, werden zweimal gebrochen. Bei der Konstruktion von Strahlengängen
fasst man beide Brechungen zu einer in der Hauptebene erfolgenden Brechung zusammen. Alle
Abstände sind auf diese Hauptebene bezogen.
Konvexlinsen sind durch zwei Kugelflächen so begrenzt, dass sie in der Mitte dicker als am Rand
sind. Parallel zur optischen Achse hindurchtretende Strahlen werden im Brennpunkt F gesammelt.
Sein Abstand von der Hauptebene ist die Brennweite f. Daher nennt man sie auch Sammellinsen.
Konkavlinsen sind durch zwei Kugelflächen so begrenzt, dass sie in der Mitte dünner sind
als am Rand. Parallel zur optischen Achse hindurchtretende Strahlen werden so gebrochen, als
kämen sie von einem vor der Linse liegenden Brennpunkt F. Sein Abstand von der Hauptebene
ist wiederum die Brennweite f, allerdings mit einem negativen Zahlenwert. Da diese Linse die
Lichtstrahlen nicht sammelt, sondern zerstreut, nennt man sie auch Zerstreuungslinse.
Im Applet Brennpunkt3 haben wir den Strahlengang in einer Sammellinse programmiert. Da die
Begrenzungsflächen kugelförmig sind, erwarten wir nur einen verschmierten Brennpunkt.
Ähnlich wie beim kugelförmigen Hohlspiegel beobachtet man eine Kaustik- Figur. Daher
werden in der sogenannten paraxialen Optik nur Lichtstrahlen betrachtet, die nahe an der
optischen Achse liegen. Im Applet können Sie die Radien R1 und R2
der Kugelflächen, den
Abstand D der Strahlen von der optischen Achse und den Brechungsindex des Glases ändern.
Bei grossen Abständen kann sogar Totalreflexion an der hinteren Ebene auftreten.
Die immer auftretenden Teilreflektionen an der vorderen und hinteren Begrenzung wurden
vernachlässigt.
Die Anwendung von Linsen in optischen Instrumenten werden in einem anderen
Tutorial
behandelt. Zum Üben der Winkelakrobatik hier noch eine kleine Aufgabe:
Aufgabe 7: Ein Lichtstrahl dringt mit einem Einfallswinkel 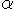 in einen kugelförmigen Wassertropfen. Wasser hat den Brechungsindex n = 1,33.
in einen kugelförmigen Wassertropfen. Wasser hat den Brechungsindex n = 1,33.
a) Wie gross ist der Einfallswinkel 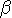 des Strahls auf der
rückwärtigen Begrenzungsfläche ? Wird der Strahl total oder nur teilweise
reflektiert ?
des Strahls auf der
rückwärtigen Begrenzungsfläche ? Wird der Strahl total oder nur teilweise
reflektiert ?
b) Der in a) reflektierte Strahl tritt an der Vorderseite des Wassertropfens wieder aus.
Wie gross ist der Winkel 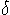 zwischen dem einfallenden und dem
austretenden Strahl als Funktion des Einfallswinkels
zwischen dem einfallenden und dem
austretenden Strahl als Funktion des Einfallswinkels 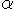 ?
?
c) Unter welchem Winkel muss der Strahl in den Wassertropfen einfallen, damit der Winkel
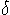 maximal wird ?
maximal wird ?
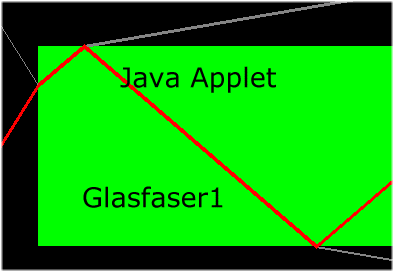 Wir knüpfen noch einmal an die Aufgabe 3 an. Dort hatten wir gesehen, dass man einen
Lichtstrahl in einer Glasstange transportieren kann, wenn man das Licht unterhalb eines gewissen
Maximalwinkels in den Stab einkoppelt. Zylindrische Glasstäbe mit Durchmessern von einigen
Millimetern bezeichnet man auch als Glasfasern. Benutzt man Plexiglas als Material, so kann
man diese Fasern auch biegen und somit das Licht über weite Strecken transportieren.
Der Biegeradius ist natürlich eingeschränkt (siehe Aufgabe 8). Zum
Schutz der eigentlichen Faser wird diese noch oft mit einem Mantel mit kleinerem
Brechungsindex umgeben.
Wir knüpfen noch einmal an die Aufgabe 3 an. Dort hatten wir gesehen, dass man einen
Lichtstrahl in einer Glasstange transportieren kann, wenn man das Licht unterhalb eines gewissen
Maximalwinkels in den Stab einkoppelt. Zylindrische Glasstäbe mit Durchmessern von einigen
Millimetern bezeichnet man auch als Glasfasern. Benutzt man Plexiglas als Material, so kann
man diese Fasern auch biegen und somit das Licht über weite Strecken transportieren.
Der Biegeradius ist natürlich eingeschränkt (siehe Aufgabe 8). Zum
Schutz der eigentlichen Faser wird diese noch oft mit einem Mantel mit kleinerem
Brechungsindex umgeben.
Aufgabe 8:Ein optisches Glasfaserkabel besteht aus einer dünnen zylindrischen
Faser mit Radius rf = 1 mm und dem Brechungsindex nf = 1,66, die von einem
dünnen äusseren Mantel mit Brechungsindex nc = 1,52 umgeben ist.
Das Kabel befindet sich in Luft mit dem Brechungsindex n0 = 1.
Wie gross ist der minimale Krümmungsradius, mit dem man das Kabel biegen darf, ohne dass
nennenswerte Lichtverluste in der Faser auftreten ?
 Bisher hatten wir nur Materialien betrachtet, in denen der Brechungsindex konstant ist.
Im Applet Brechung2 hatten wir eine Anordnung mit 10 Glasplatten studiert, wobei der
Brechungsindex jeder einzelnen Platte als Funktion des Abstandes von der optischen Achse
linear abnahm. Wir gehen jetzt über zu Materialien mit einem kontinuierlich veränderten
Brechungsindex. Technisch hergestellt werden diese Gläser durch unterschiedliche
Dotierung mit Fremdatomen.
Der Brechungsindex sei nur vom Abstand von der optischen Achse abhängig,
diesen Abstand bezeichnen wir im folgenden mit r, die Achse mit z. Wie wir in Aufgabe 9
zeigen werden, folgt der Lichtstrahl in solchen Materialen einer geometrischen Bahn, die
durch die Differentialgleichung
Bisher hatten wir nur Materialien betrachtet, in denen der Brechungsindex konstant ist.
Im Applet Brechung2 hatten wir eine Anordnung mit 10 Glasplatten studiert, wobei der
Brechungsindex jeder einzelnen Platte als Funktion des Abstandes von der optischen Achse
linear abnahm. Wir gehen jetzt über zu Materialien mit einem kontinuierlich veränderten
Brechungsindex. Technisch hergestellt werden diese Gläser durch unterschiedliche
Dotierung mit Fremdatomen.
Der Brechungsindex sei nur vom Abstand von der optischen Achse abhängig,
diesen Abstand bezeichnen wir im folgenden mit r, die Achse mit z. Wie wir in Aufgabe 9
zeigen werden, folgt der Lichtstrahl in solchen Materialen einer geometrischen Bahn, die
durch die Differentialgleichung
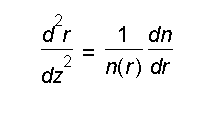
beschrieben wird.
Mit der Annahme, dass r sehr viel kleiner als a ist, erhalten wir die einfache Differentialgleichung
Dieses ist aber nichts anderes als die Differentialgleichung der harmonischen Schwingung.
Die Lösung ist
Bei rechnerischen Anwendungen kann man also davon ausgehen, dass n0 zwischen 1.5 und
1.8 liegt, die gesamte Änderung des Brechungsindex von der optischen Achse bis zum Rand aber nur
in der Grössenordnung einiger Prozente ist.
gegeben. D ist die Dicke der Linse. Für grosse Werte für r(0) beobachtet man wieder
eine Kaustik- Figur.
R = 6400 km ist der Erdradius, r der Abstand vom Erdmittelpunkt und a = 8,7 km die Höhe über
Erdoberfläche, bei der q = 0,0003 auf den e-ten Teil abgefallen ist. Der Brechungsindex
von Luft ist auf der Erdoberfläche also 1,0003. n(r)-1 ist inbesondere der Dichte
der Luft proportional. Licht läuft in der Erdathmosphäre also auf gekrümmten
Bahnen, wird insbesondere von der Erdoberfläche angezogen. Diese Beobachtung
machen Sie im Prinzip jeden Tag. Sie können die Sonne noch sehen, auch wenn sie schon längst
hinter dem Horizont verschwunden ist. Da wir die oben angegebene Differentialgleichung für
diesen Brechungsindex nicht analytisch lösen können, benutzen wir im Applet ein
numerisches Integrationsverfahren. Dadurch verlangsamt sich die Berechnung der Lichtbahn
natürlich erheblich. Wir stellen dann im Applet die Frage, ob wir den Lichtstrahl auf
einer Kreisbahn um die Erde lenken können. Mit einem Wert von q = 0,0003 ist dieses
sicher nicht möglich. Auf einer Distanz von 1000 km sieht man kaum eine Ablenkung des
Lichtstrahls. Erhöht man allerdings den Wert von q auf etwa 0,00135, so läuft das
Licht auf einer exakten Kreisbahn um die Erde. Man müsste die Dichte der Luft
also etwa auf das 4,5- fache vergrössern.
<Harm.Fesefeldt@harfesoft.de>
Aufgabe 9: In einem Glasfaserkabel ist der Brechungsindex n(r) stetig vom Abstand r
von der optischen Achse abhängig. Die Ableitung dn/dr existiert für alle r < R mit
dem Radius R der Faser. Zeigen Sie die Gültigkeit der oben angegebenen allgemeinen
Differentialgleichung für die Bahn r(z) des Lichtstrahls.
Anleitung: Wenden Sie das Brechungsgestz auf eine Grenzfläche an, bei der sich der
Brechungsindex von n(r) auf n(r+dr) ändert. Dabei ändert sich die Richtung des
Lichtstrahls gegenüber der optischen Achse von 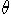 nach
nach
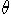 +d
+d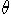 . Für diesen Winkel
gilt sin(d
. Für diesen Winkel
gilt sin(d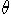 )=d
)=d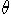 ,
cos(d
,
cos(d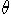 )=1 und
)=1 und
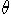 =tan(
=tan(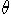 )=dr/dz. Vernachlässigen
Sie infinitesimale Grössen zweiter Ordnung, diese verschwinden sowieso beim
Grenzübergang dr -> 0.
)=dr/dz. Vernachlässigen
Sie infinitesimale Grössen zweiter Ordnung, diese verschwinden sowieso beim
Grenzübergang dr -> 0.
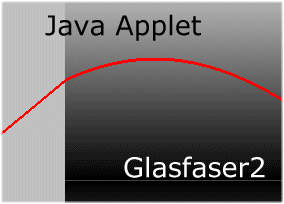
Wir bauen jetzt ein Glasfaserkabel, bei dem der Brechungsindex quadratisch in r abnimmt:
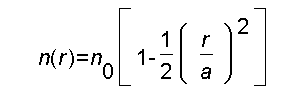
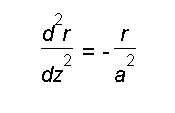
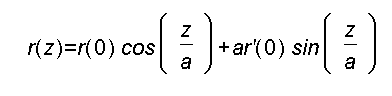
Das Licht wird also im Abstand r(0) von der optischen Achse mit der Steigung r'(0) in das Kabel
eingekoppelt und schwingt dann im Kabel um die optische Achse herum. Der grosse Vorteil dieser
Kabel ist natürlich, dass das Licht keinen Kontakt mehr mit den Begrenzungsflächen
hat und daher die Verluste extrem klein gehalten werden. Dieses Kabel zeigen wir
im Applet Glasfaser2. Sie können den Parameter a, den Einfallswinkel
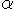 und den Startwert r(0) ändern. Das Programm berechnet
mit Hilfe des Brechungsgesetzes den Startwert für r'(0). Der Schwärzungsgrad
gibt die Grösse des Brechungsindex an. Man sieht also, dass der Lichtstrahl dem
Gradienten des Brechungsindex folgt.
und den Startwert r(0) ändern. Das Programm berechnet
mit Hilfe des Brechungsgesetzes den Startwert für r'(0). Der Schwärzungsgrad
gibt die Grösse des Brechungsindex an. Man sieht also, dass der Lichtstrahl dem
Gradienten des Brechungsindex folgt.
 Im folgenden Applet machen wir jetzt das Glasfaserkabel extrem kurz, einige Millimeter,
und strahlen parallel zur optischen Achse Licht ein. Das Licht wird zur optischen
Achse hin abgelenkt, trifft auf die hintere Begrenzungsfläche, wird noch einmal gebrochen
und tritt dann in die Luft aus. Im Applet können Sie beobachten, dass diese Anordung
ein System mit einem Brennpunkt ist. Wir haben also eine Linse konstruiert. Rechnerisch ist die
Brennweite durch (siehe Aufgabe 10)
Im folgenden Applet machen wir jetzt das Glasfaserkabel extrem kurz, einige Millimeter,
und strahlen parallel zur optischen Achse Licht ein. Das Licht wird zur optischen
Achse hin abgelenkt, trifft auf die hintere Begrenzungsfläche, wird noch einmal gebrochen
und tritt dann in die Luft aus. Im Applet können Sie beobachten, dass diese Anordung
ein System mit einem Brennpunkt ist. Wir haben also eine Linse konstruiert. Rechnerisch ist die
Brennweite durch (siehe Aufgabe 10)
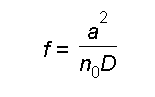
Aufgabe 10: Berechnen Sie die Brennweite der planaren Linse des Applets Glasfaser3. Bedenken Sie,
dass man für kleine Werte von z/a die Cosinus- und Sinusfunktion in Reihen entwickeln kann und
berücksichtigen Sie die zusätzliche Brechung an der Rückseite der Linse.
Aufgabe 11: Eine kreisförmige ebene Glasplatte mit der Dicke D soll als Linse
mit einer Brennweite f benutzt werden. r sei der Abstand von der Achse der Scheibe. Bestimmen
Sie mit Hilfe des Fermatschen Prinzips die hierfür notwendige r- Abhängigkeit des
Brechungsindex. Vergleichen Sie Ihre Lösung mit dem Ergebnis von Aufgabe 10.
 Die Lufthülle der Erde hat mit wachsender Höhe einen exponentiell abfallenden
Brechungsindex:
Die Lufthülle der Erde hat mit wachsender Höhe einen exponentiell abfallenden
Brechungsindex:
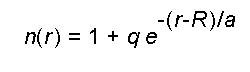
Aufgabe 12: Zeigen Sie mit Hilfe des Fermatschen Prinzips, dass das Licht auf der
Erdoberfläche auf einer Kreisbahn laufen würde wenn man die Dichte der Luft
auf das 4,5- fache vergrössern könnte.
(Das Password ist der Name eines Mathematikers, der in diesem Tutorial mehrmals genannt wurde.)
Literatur:
Hecht/Zajac, Optics, Addison Wesley Publishing Company, 1982
James C. Daly, Fiber Optics, CRC Press, 1986
Damit beschliessen wir unser Tutorial über das Fermat'sche Prinzip und seine Anwendung
auf Reflexion und Brechung. Ich hoffe, es hat Ihnen
Spass gemacht. Vielleicht haben Sie auch Einiges gelernt. Falls Sie Fehler finden oder
Verbesserungsvorschläge haben, schreiben Sie an
Das gesamte Tutorial einschliesslich aller Java Class Files und der Source Codes können
Sie auch als Zip- File herunterladen. Ich bitte allerdings
darum, die Creative Commons- Lizenz
zu beachten.