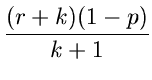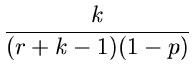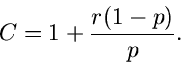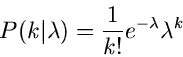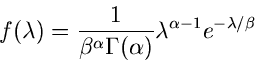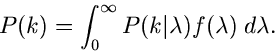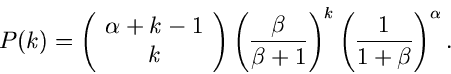Simulation diskreter Veränderlicher
Vorbemerkung.
Wir hatten die Simulation diskreter Veränderlicher schon im
Zusammenhang mit der Simualtion kontinuierlicher Veränderlicher kurz
angesprochen, und tatsächlich, die meisten Verfahren lassen sich ohne
weiteres auf diskrete Veränderliche übertragen. Hinzu kommen aber einige
Besonderheiten, die wir im folgenden Unterkapitel diskutieren wollen. Im
Mittelpunkt unserer Betrachtungen wird die inverse Transformationsmethode
stehen, die bei diskreten Veränderlichen immer anwendbar ist.
Verwerfungsmethoden spielen zwar eine weniger wichtige Rolle, jedoch gibt
es auch bei diskreten Veränderlichen einige schöne Anwendungsbeispiele.
Hinzu kommen dagegen Methoden der Diskretisierung kontinuierlicher
Veränderlicher und insbesondere Approximationen durch kontinuierliche
Funktionen. Auch die Simulation des verbalen Wortmodells führt bei diskreten
Veränderlichen zu außerordentlich schönen und schnellen Algorithmen.
Inverse Transformationsmethode.
Die Wahrscheinlichkeitsverteilung 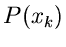 einer diskreten Veränderlichen
einer diskreten Veränderlichen
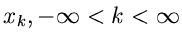 , mit ganzzahligem
, mit ganzzahligem  , kann in praktischen
Anwendungen immer auf eine Wahrscheinlichkeitsverteilung
, kann in praktischen
Anwendungen immer auf eine Wahrscheinlichkeitsverteilung 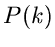 mit einer
positiven ganzzahligen Veränderlichen
mit einer
positiven ganzzahligen Veränderlichen  transformiert werden. Wir legen
daher im folgenden immer eine Verteilung
transformiert werden. Wir legen
daher im folgenden immer eine Verteilung 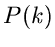 mit
mit 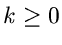 zugrunde.
Die integrale Verteilung ist
zugrunde.
Die integrale Verteilung ist
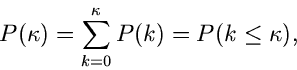 |
(1) |
und die inverse Transformationsmethode lautet: Erzeuge ![$u \in U[0,1]$](img7.gif) und bestimme
und bestimme 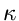 so, daß
so, daß
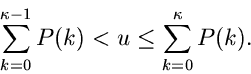 |
(2) |
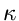 ist dann eine Veränderliche der Wahrscheinlichkeitsverteilung
ist dann eine Veränderliche der Wahrscheinlichkeitsverteilung
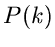 .
.
Wir haben in unseren bisherigen Betrachtungen jedoch nicht über optimale
Algorithmen zur Lösung der Ungleichung (2) gesprochen. Das einfachste
Verfahren basiert natürlich auf den Rekursionsrelationen
wobei 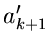 und
und 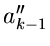 im allgemeinen einfache Funktionen von
im allgemeinen einfache Funktionen von  sind.
Mit Hilfe dieser Funktion
sind.
Mit Hilfe dieser Funktion 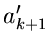 kann man das Verfahren folgendermaßen
formulieren:
kann man das Verfahren folgendermaßen
formulieren:
1. Erzeuge ![$u \in U[0,1]$](img7.gif) , berechne
, berechne
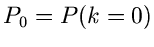 und setze
und setze
2. Wenn 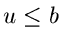 , dann ist
, dann ist  eine Veränderliche der
Wahrscheinlichkeitsverteilung
eine Veränderliche der
Wahrscheinlichkeitsverteilung 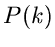 . Wenn dagegen
. Wenn dagegen 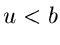 , dann berechne
, dann berechne
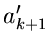 und setze
und setze
und gehe zurück zu Punkt 2.
Dieser Algorithmus ist natürlich nur ein Spezialfall des allgemeineren
Verfahrens, bei dem man bei irdendeinem Wert 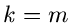 mit den
Vergleichsoperationen beginnt. Das Verfahren lautet dann entsprechend:
mit den
Vergleichsoperationen beginnt. Das Verfahren lautet dann entsprechend:
1. Erzeuge ![$u \in U[0,1]$](img7.gif) und setze
und setze
Falls 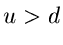 , fahre fort bei Punkt 3, sonst bei Punkt 2.
, fahre fort bei Punkt 3, sonst bei Punkt 2.
2. Setze
Falls 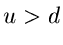 , so ist
, so ist  eine Veränderliche der Wahrscheinlichkeitsverteilung
eine Veränderliche der Wahrscheinlichkeitsverteilung
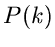 . Wenn dagegen
. Wenn dagegen 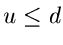 , dann berechne
, dann berechne 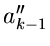 und setze
und setze
und gehe zurück zu Punkt 2.
3. Berechne 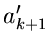 und setze
und setze
Falls 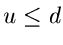 , so ist
, so ist  eine Veränderliche von
eine Veränderliche von 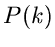 , sonst gehe
zurück zu Punkt 3.
, sonst gehe
zurück zu Punkt 3.
Entscheidend für die Schnelligkeit dieses allgemeineren Verfahrens ist
natürlich einmal die Berechnung des Startwertes für
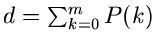 . Hierfür kann man im allgemeinen keinen analytischen
Ausdruck angeben, sodaß die Summe tatsächlich aus
. Hierfür kann man im allgemeinen keinen analytischen
Ausdruck angeben, sodaß die Summe tatsächlich aus 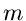 arithmetischen
Operationen berechnet werden muß. Dieses kann die Vorteile, die im folgenden
diskutiert werden, durchaus wieder zunichte machen. Zweitens hängt die
Schnelligkeit des Verfahrens von der Anzahl der Vergleichsoperationen ab.
Diese Anzahl ist offensichtlich gegeben durch
arithmetischen
Operationen berechnet werden muß. Dieses kann die Vorteile, die im folgenden
diskutiert werden, durchaus wieder zunichte machen. Zweitens hängt die
Schnelligkeit des Verfahrens von der Anzahl der Vergleichsoperationen ab.
Diese Anzahl ist offensichtlich gegeben durch
gegeben. Der Erwartungswert von 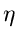 ist
ist
mit
Ähnlich wie bei den Verwerfungsverfahren nennen wir die Größe 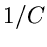 die Erfolgswahrscheinlichkeit:
die Erfolgswahrscheinlichkeit:
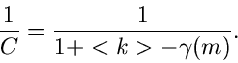 |
(3) |
Wie man sich leicht klarmachen kann, kann 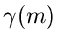 positive wie negative
Werte annehmen. Den optimalen Wert für
positive wie negative
Werte annehmen. Den optimalen Wert für 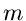 erhält man aus dem folgenden
Satz:
erhält man aus dem folgenden
Satz:
Sei 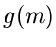 und der Median
und der Median 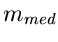 definiert durch
definiert durch
Dann ist der optimale Startwert 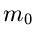 durch
durch
Vorraussetzung für beide Fälle ist jedoch, daß
In allen Programmbeispielen werden wir mit 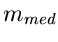 als Parameter
beginnen, dann ist der Startwert
als Parameter
beginnen, dann ist der Startwert 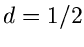 . Es muß aber betont werden, daß dieses Verfahren
nicht notwendig das optimale Verfahren ist.
. Es muß aber betont werden, daß dieses Verfahren
nicht notwendig das optimale Verfahren ist.
Verwerfungsverfahren.
Die Verwerfungsverfahren werden ganz analog wie bei kontinuierlichen
Veränderlichen eingeführt. Wir stellen die Wahrscheinlichkeitsverteilung
in der Form
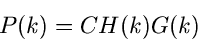 |
(4) |
mit
dar. Hierbei sollte 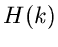 eine möglichst gute Approximation von
eine möglichst gute Approximation von 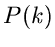 sein
und wir sollten für
sein
und wir sollten für 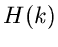 bereits einen Simulations- Algorithmus besitzen.
Das Verfahren lautet also: Erzeuge
bereits einen Simulations- Algorithmus besitzen.
Das Verfahren lautet also: Erzeuge ![$u \in U[0,1]$](img7.gif) und eine
Veränderliche
und eine
Veränderliche  aus der Wahrscheinlichkeitsverteilung
aus der Wahrscheinlichkeitsverteilung 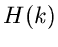 .
Wenn dann
.
Wenn dann
akzeptiere  als Veränderliche der Wahrscheinlichkeitsverteilung
als Veränderliche der Wahrscheinlichkeitsverteilung
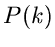 , sonst beginne von vorne.
, sonst beginne von vorne.
Besonders einfach ist bei diskreten Veränderlichen das von Neumannsche
Verfahren, sofern die Veränderliche  auf endlich viele Werte
beschränkt ist, d.h.
auf endlich viele Werte
beschränkt ist, d.h. 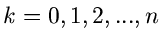 . Für
. Für 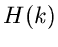 setzen wir die
diskrete Gleichverteilung
setzen wir die
diskrete Gleichverteilung
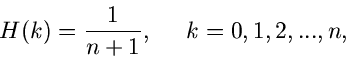 |
(5) |
und für 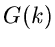 die Funktion
die Funktion
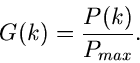 |
(6) |
Das Verfahren lautet: Erzeuge
![$u_{1},u_{2} \in U[0,1]$](img73.gif) und bestimme
und bestimme
 gemäß
gemäß
Wenn dann
akzeptiere  als Veränderliche der Wahrscheinlichkeitsverteilung
als Veränderliche der Wahrscheinlichkeitsverteilung 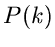 ,
sonst beginne von vorne.
,
sonst beginne von vorne.
Diskretisierung kontinuierlicher Funktionen.
Jede Wahrscheinlichkeitsverteilung kann als Integral über eine kontinuierliche
Dichtefunktion dargestellt werden:
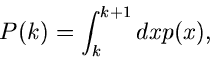 |
(7) |
mit
Für große Werte von  kann das Inegral approximiert werden durch
(man beachte:
kann das Inegral approximiert werden durch
(man beachte: 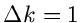 )
)
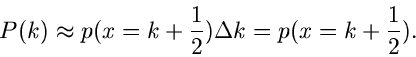 |
(8) |
Das Verfahren lautet: Erzeuge eine Veränderliche 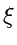 aus der
Dichtefunktion
aus der
Dichtefunktion 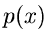 und bestimme
und bestimme  gemäß
gemäß
 ist dann eine Veränderliche aus
ist dann eine Veränderliche aus 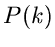 .
.
Simulation des verbalen Wortmodells.
Bei diskreten Veränderlichen liefert die Übertragung des verbalen
Wortmodells in ein Rechnerprogramm häufig sehr schnelle Algorithmen.
Ein Beispiel möge dieses belegen. Eine Veränderliche der
Binominal- oder Bernoulli- Verteilung hatten wir definiert als Anzahl der
positiven Versuche in einer Reihe von insgesamt 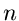 Versuchen, wobei der Einzelversuch mit einer Wahrscheinlichkeit
Versuchen, wobei der Einzelversuch mit einer Wahrscheinlichkeit 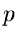 zu
einem positiven Ergebnis führt. Wir simulieren den Einzelversuch durch
den einmaligen Aufruf des Zufallszahlen- Generators. Der Versuch wird als
positiv bewertet, sofern die Zufallszahl
zu
einem positiven Ergebnis führt. Wir simulieren den Einzelversuch durch
den einmaligen Aufruf des Zufallszahlen- Generators. Der Versuch wird als
positiv bewertet, sofern die Zufallszahl 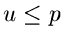 . Diesen Einzelversuch
wiederholen wir
. Diesen Einzelversuch
wiederholen wir 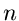 -mal und zählen die Anzahl
-mal und zählen die Anzahl  der positiven Ereignisse.
Die Zahl
der positiven Ereignisse.
Die Zahl  ist dann offenbar eine Veränderliche der Binominalverteiling
ist dann offenbar eine Veränderliche der Binominalverteiling
![$B[p,n]$](img86.gif) . Der Rechenaufwand in diesem Algorithmus besteht im wesentlichen
aus der Erzeugung von
. Der Rechenaufwand in diesem Algorithmus besteht im wesentlichen
aus der Erzeugung von 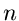 Zufallszahlen aus
Zufallszahlen aus ![$U[0,1]$](img87.gif) . Ähnliche Wortmodelle
können für fast alle diskreten Veränderlichen formuliert werden.
. Ähnliche Wortmodelle
können für fast alle diskreten Veränderlichen formuliert werden.
Bevor wir fortfahren, sollten Sie das
Applet über die diskreten Verteilungen
auf Ihren Bildschirm laden.
Binomial-Verteilung
Wir bezeichnen die Binomialverteilung
mit 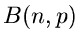 . Die Methode JBinomial1 beschreibt das Wortmodell. Wir erzeugen uns
. Die Methode JBinomial1 beschreibt das Wortmodell. Wir erzeugen uns 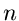 Zufallszahlen
Zufallszahlen 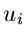 mit
dem Gleichverteilungsgenerator Ranmar und fragen nach der Anzahl der Zahlen
mit
dem Gleichverteilungsgenerator Ranmar und fragen nach der Anzahl der Zahlen  mit
mit 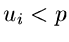 .
In der Methode JBinomial2 haben wir die inverse Transformationsmethode realisiert. Hierfür wurden
die folgenden Ausdrücke berechnet:
.
In der Methode JBinomial2 haben wir die inverse Transformationsmethode realisiert. Hierfür wurden
die folgenden Ausdrücke berechnet:
Die eckigen Klammer ![$[...]$](img97.gif) bedeuten hier und im folgenden die Abrundung auf eine ganze Zahl.
Die Anzahl der Vergleichsoperationen ist im Mittel durch
bedeuten hier und im folgenden die Abrundung auf eine ganze Zahl.
Die Anzahl der Vergleichsoperationen ist im Mittel durch
gegeben. Die Verteilung dieser Zahlen zeigen wir im Applet im Plot RandomCalls.
Für große Werte von 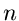 kann die Binomial- Verteilung durch eine Normalverteilung approximiert werden
(siehe auch Kap.1 dieses Tutorials). Die Größe
kann die Binomial- Verteilung durch eine Normalverteilung approximiert werden
(siehe auch Kap.1 dieses Tutorials). Die Größe
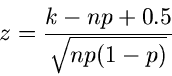 |
(9) |
ist näherungsweise normal verteilt, mit einer Standardabweichung von 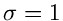 . In der Methode
JBinomial3 erzeugen wir uns daher eine normal verteilte Variable
. In der Methode
JBinomial3 erzeugen wir uns daher eine normal verteilte Variable  aus
aus ![$N[0,1]$](img102.gif) und lösen
die Gleichung (9) nach
und lösen
die Gleichung (9) nach  auf:
auf:
Poisson- Verteilung
Wir schreiben die Poisson- Verteilung in der Form
und bezeichnen diese mit ![$P[\lambda]$](img105.gif) . Unser erstes Modell kommt aus dem radioaktiven Zerfall.
Wenn das Zeitintervall
. Unser erstes Modell kommt aus dem radioaktiven Zerfall.
Wenn das Zeitintervall 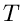 zwischen zwei Zerfällen aus einer Exponentialverteilung
zwischen zwei Zerfällen aus einer Exponentialverteilung ![$E[1/\lambda]$](img107.gif) ist,
dann ist die Anzahl der Zerfälle in der Zeiteinheit durch eine Poissonverteilung
ist,
dann ist die Anzahl der Zerfälle in der Zeiteinheit durch eine Poissonverteilung ![$P[\lambda]$](img105.gif) gegeben. Mathematisch können wir diesen Sachverhalt formulieren als
gegeben. Mathematisch können wir diesen Sachverhalt formulieren als
mit
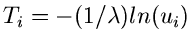 aus
aus ![$E[1/\lambda]$](img107.gif) und
und 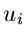 aus
aus ![$U[0,1]$](img87.gif) . Daher gilt auch
. Daher gilt auch
oder
Der in JPoisson1 entwickelte Algorithmus basiert auf dieser letzten Ungleichung.
In JPoisson2 wird wiederum die inverse Transformationsmethode angewendet. Die entsprechenden Formeln
sind
Die Anzahl der notwendigen Vergleichsoperationen ist ähnlich wie bei der Binomial- Verteilung durch
gegeben. Auch die Poisson- Verteilung kann für große Werte von 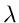 durch eine Normalverteilung approximiert
werden. Die Variable
durch eine Normalverteilung approximiert
werden. Die Variable
ist dann aus ![$N[0,1]$](img102.gif) . Wir lösen wieder nach
. Wir lösen wieder nach  auf und erhalten
auf und erhalten
JPoisson3 zeigt diesen Algorithmus.
Geometrische Verteilung
Die geometrische Verteilung
wird mit ![$Ge[p]$](img120.gif) abgekürzt und beschreibt die Anzahl der Versuche in einem Bernoulli- Experiment bis zum ersten
erfogreichen Versuch. Dieses Wortmodell ist in JGeometric1 in einen Simulations- Algorithmus umgesetzt worden.
In der inversen Transformationsmethode in JGeometric2 starten wir die Vergleichsoperationen ausnahmsweise
bei
abgekürzt und beschreibt die Anzahl der Versuche in einem Bernoulli- Experiment bis zum ersten
erfogreichen Versuch. Dieses Wortmodell ist in JGeometric1 in einen Simulations- Algorithmus umgesetzt worden.
In der inversen Transformationsmethode in JGeometric2 starten wir die Vergleichsoperationen ausnahmsweise
bei
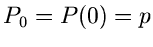 und benutzen
und benutzen
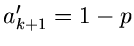 . Die mittlere Zahl der Vergleichsoperationen ist dann
. Die mittlere Zahl der Vergleichsoperationen ist dann
Ein sehr schöner Algorithmus folgt aus der Verbindung der geometrischen Verteilung und der Exponentialverteilung.
Wenn 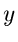 eine Variable aus
eine Variable aus ![$E[\beta]$](img125.gif) ist, dann gilt
ist, dann gilt
Der rechts stehende Ausdruck ist aber nichts anderes als
![$Ge[p = 1-e^{-y/\beta}]$](img127.gif) . Wir erzeugen also eine
Variable
. Wir erzeugen also eine
Variable 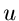 aus einer Gleichverteilung und berechnen
aus einer Gleichverteilung und berechnen
 ist dann eine Varible aus der geometrischen Verteilung. Der Algorithmus ist in JGeometric3 gezeigt.
ist dann eine Varible aus der geometrischen Verteilung. Der Algorithmus ist in JGeometric3 gezeigt.
Negative Binomialverteilung
Als letztes diskutieren wir noch die negative Binomialverteilung ![$NB[r,p]$](img130.gif) :
:
Hier ist  die Anzahl der positiven Versuche in einem Bernoulli- Experiment bis zum Auftreten von
die Anzahl der positiven Versuche in einem Bernoulli- Experiment bis zum Auftreten von 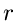 negativen Versuchen.
Dieses ist exakt das Wortmodell in JNegBinomial1. Für die inverse Transformationsmethode in JNegBinomial2
haben wir die folgenden Ausdrücke berechnet:
negativen Versuchen.
Dieses ist exakt das Wortmodell in JNegBinomial1. Für die inverse Transformationsmethode in JNegBinomial2
haben wir die folgenden Ausdrücke berechnet:
Die mittlere Anzahl der Vergleichsoperationen ist
Der dritte Algorithmus ist hergeleitet aus der Verbindung der negativen Binomialverteilung mit der Gammaverteilung
und der Poissonverteilung. Wir nehmen an, daß der Parameter 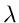 in der Poissonverteilung
in der Poissonverteilung
mit einer Gammaverteilung variiert:
Dann erhalten wir die gefaltete Verteilung
Die Berechnung führt auf
Also ist  eine Variable aus
eine Variable aus
![$NB[\alpha,1/(1+\beta)]$](img143.gif) . Unser Algorithmus lautet also: Erzeuge
. Unser Algorithmus lautet also: Erzeuge 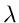 aus
Gammaverteilung
aus
Gammaverteilung ![$G[r,p/(1-p)]$](img144.gif) und
und  aus der Poissonverteilung
aus der Poissonverteilung ![$P[\lambda]$](img105.gif) . Der Source- Code wird in JNegBinomial3 gezeigt.
Der letzte Algorithmus in JNegBinomial4 benutzt die Verbindung zwischen der negativen Binomialverteilung und
der geometrischen Verteilung. Der Algorithmus lautet: Erzeuge
. Der Source- Code wird in JNegBinomial3 gezeigt.
Der letzte Algorithmus in JNegBinomial4 benutzt die Verbindung zwischen der negativen Binomialverteilung und
der geometrischen Verteilung. Der Algorithmus lautet: Erzeuge 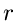 Variable
Variable
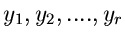 aus der
geometrischen Verteilung
aus der
geometrischen Verteilung ![$Ge[p]$](img120.gif) und setze
und setze
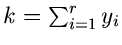 .
.
Schlußbemerkung
Hiermit wollen wir unser Tutorial über Statistik mit Schwerpunkt auf Simulationsalgorithmen zufälliger Veränderlicher
beschliessen. Der aufmerksame Leser sollte hiermit in der Lage sein, auch für andere Veränderliche effektive
Algorithmen zu entwickeln. Die Simulation ist heute eine wichtige Methode in allen Gebieten der Wissenschaften
geworden.
Harm Fesefeldt
2006-07-11
![]() einer diskreten Veränderlichen
einer diskreten Veränderlichen
![]() , mit ganzzahligem
, mit ganzzahligem ![]() , kann in praktischen
Anwendungen immer auf eine Wahrscheinlichkeitsverteilung
, kann in praktischen
Anwendungen immer auf eine Wahrscheinlichkeitsverteilung ![]() mit einer
positiven ganzzahligen Veränderlichen
mit einer
positiven ganzzahligen Veränderlichen ![]() transformiert werden. Wir legen
daher im folgenden immer eine Verteilung
transformiert werden. Wir legen
daher im folgenden immer eine Verteilung ![]() mit
mit ![]() zugrunde.
Die integrale Verteilung ist
zugrunde.
Die integrale Verteilung ist
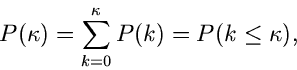
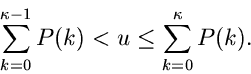
![]() mit den
Vergleichsoperationen beginnt. Das Verfahren lautet dann entsprechend:
mit den
Vergleichsoperationen beginnt. Das Verfahren lautet dann entsprechend:
![]() und setze
und setze
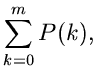
![]() . Hierfür kann man im allgemeinen keinen analytischen
Ausdruck angeben, sodaß die Summe tatsächlich aus
. Hierfür kann man im allgemeinen keinen analytischen
Ausdruck angeben, sodaß die Summe tatsächlich aus ![]() arithmetischen
Operationen berechnet werden muß. Dieses kann die Vorteile, die im folgenden
diskutiert werden, durchaus wieder zunichte machen. Zweitens hängt die
Schnelligkeit des Verfahrens von der Anzahl der Vergleichsoperationen ab.
Diese Anzahl ist offensichtlich gegeben durch
arithmetischen
Operationen berechnet werden muß. Dieses kann die Vorteile, die im folgenden
diskutiert werden, durchaus wieder zunichte machen. Zweitens hängt die
Schnelligkeit des Verfahrens von der Anzahl der Vergleichsoperationen ab.
Diese Anzahl ist offensichtlich gegeben durch
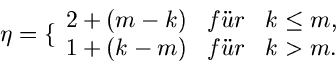
![\begin{displaymath}
C = <\eta> = \sum_{k=0}^{m} [2+(m-k)] P(k) - \sum_{k=m+1}^{\infty}
[1+(k-m)] P(k) = 1 + <k> - \gamma(m),
\end{displaymath}](img47.gif)
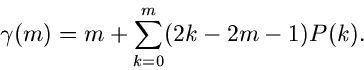
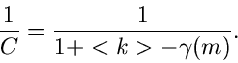
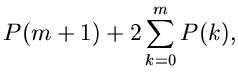
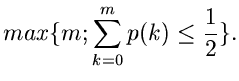
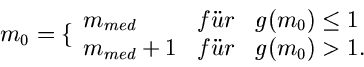
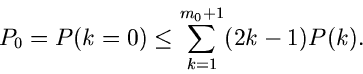
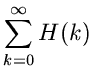
![]() auf endlich viele Werte
beschränkt ist, d.h.
auf endlich viele Werte
beschränkt ist, d.h. ![]() . Für
. Für ![]() setzen wir die
diskrete Gleichverteilung
setzen wir die
diskrete Gleichverteilung
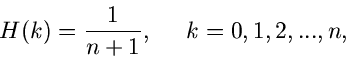
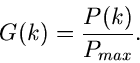
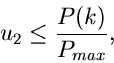
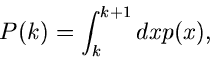
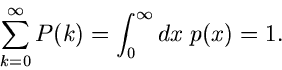
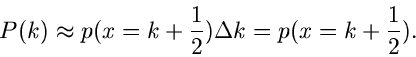
![]() Versuchen, wobei der Einzelversuch mit einer Wahrscheinlichkeit
Versuchen, wobei der Einzelversuch mit einer Wahrscheinlichkeit ![]() zu
einem positiven Ergebnis führt. Wir simulieren den Einzelversuch durch
den einmaligen Aufruf des Zufallszahlen- Generators. Der Versuch wird als
positiv bewertet, sofern die Zufallszahl
zu
einem positiven Ergebnis führt. Wir simulieren den Einzelversuch durch
den einmaligen Aufruf des Zufallszahlen- Generators. Der Versuch wird als
positiv bewertet, sofern die Zufallszahl ![]() . Diesen Einzelversuch
wiederholen wir
. Diesen Einzelversuch
wiederholen wir ![]() -mal und zählen die Anzahl
-mal und zählen die Anzahl ![]() der positiven Ereignisse.
Die Zahl
der positiven Ereignisse.
Die Zahl ![]() ist dann offenbar eine Veränderliche der Binominalverteiling
ist dann offenbar eine Veränderliche der Binominalverteiling
![]() . Der Rechenaufwand in diesem Algorithmus besteht im wesentlichen
aus der Erzeugung von
. Der Rechenaufwand in diesem Algorithmus besteht im wesentlichen
aus der Erzeugung von ![]() Zufallszahlen aus
Zufallszahlen aus ![]() . Ähnliche Wortmodelle
können für fast alle diskreten Veränderlichen formuliert werden.
. Ähnliche Wortmodelle
können für fast alle diskreten Veränderlichen formuliert werden.
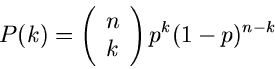
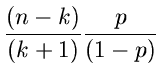
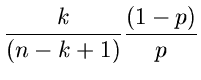
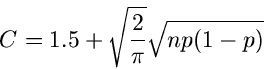
![]() kann die Binomial- Verteilung durch eine Normalverteilung approximiert werden
(siehe auch Kap.1 dieses Tutorials). Die Größe
kann die Binomial- Verteilung durch eine Normalverteilung approximiert werden
(siehe auch Kap.1 dieses Tutorials). Die Größe
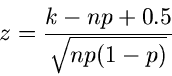
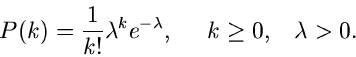
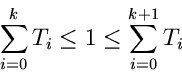
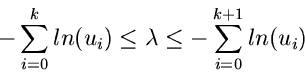
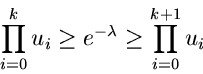
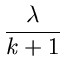
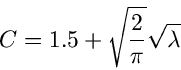
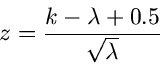
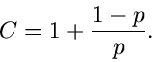
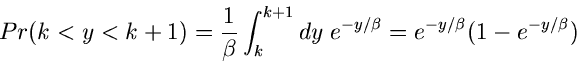
![$Ge[p = 1-e^{-y/\beta}]$](img127.gif) . Wir erzeugen also eine
Variable
. Wir erzeugen also eine
Variable ![\begin{displaymath}
k = \left[ \frac{ln(u)}{ln(1-p)} \right].
\end{displaymath}](img129.gif)
![]() :
:
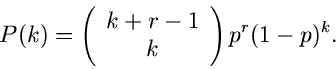
![$\displaystyle \left[ \frac{(r-p)(1-p)}{p} \right]$](img133.gif)