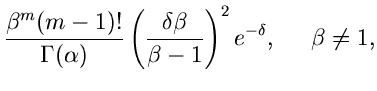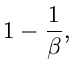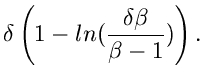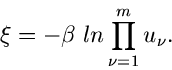Kontinuierliche Verteilungen I
Übersicht
In den nächsten drei Abschnitten des vorliegenden Kapitels
werden wir noch einmal
eine Zusammenstellung der wichtigsten Algorithmen zur Simulation einfacher
zufälliger Veränderlicher geben. Die hier getroffene Auswahl wird sicherlich
nicht erschöpfend sein. Sie soll vielmehr dem Leser einen Eindruck davon
vermitteln, wie vielfältig die Ideen und Methoden sind, und damit den Leser
auch zu eigener Entwicklungsarbeit anregen.
Den Source Code zu allen Algorithmen finden Sie in unsreren Java- Applets.
Zur klareren Bezeichnung der Verteilungen führen wir noch einige
mnemotechnische Abkürzungen ein. So werden wir z.B. eine gleichverteilte
Veränderliche aus dem Zahlenintervall von 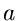 bis
bis 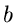 mit
mit
![$u \in U[a,b]$](img3.gif) kennzeichnen. Eine normalverteilte Veränderliche
entsprechend mit
kennzeichnen. Eine normalverteilte Veränderliche
entsprechend mit
![$x \in N[a,\sigma ]$](img4.gif) . Die Dichtefunktion bzw
Wahrscheinlichkeitsverteilung wird dabei mit einem mnemotechnisch einfachen
Symbol (
. Die Dichtefunktion bzw
Wahrscheinlichkeitsverteilung wird dabei mit einem mnemotechnisch einfachen
Symbol (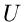 = uniform,
= uniform, 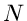 = normal) gekennzeichnet, die Parameter der
Verteilung in eckigen Klammern angefügt. Eine Zusammenstellung der wichtigsten
kontinuierlichen Verteilungen und ihrer Symbole ist in Tabelle 1 gelistet.
Für die folgenden Erörterungen verweisen wir auf das erste
Applet dieses Kapitels.
= normal) gekennzeichnet, die Parameter der
Verteilung in eckigen Klammern angefügt. Eine Zusammenstellung der wichtigsten
kontinuierlichen Verteilungen und ihrer Symbole ist in Tabelle 1 gelistet.
Für die folgenden Erörterungen verweisen wir auf das erste
Applet dieses Kapitels.
Tabelle:
Zusammenstellung der wichtigsten Verteilungen kontnuierlicher
Veränderlicher und ihrer mnemotechnischen Symbole.
| Dichtefunktion |
|
Symbol |
Bezeichnung der Verteilung |
| |
|
|
|
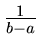 |
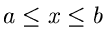 |
![$U[a,b]$](img9.gif) |
Gleichverteilung |
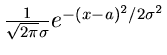 |
|
![$N[a,\sigma ]$](img11.gif) |
Normalverteilung |
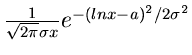 |
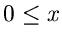 |
![$LN[a,\sigma ]$](img14.gif) |
Lognormalverteilung |
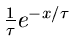 |
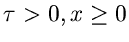 |
![$E[\tau]$](img17.gif) |
Exponentialverteilung |
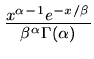 |
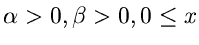 |
![$G[\alpha, \beta]$](img20.gif) |
Gammaverteilung |
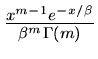 |
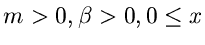 |
![$Er[m,\beta]$](img23.gif) |
Erlang- Verteilung |
Um die HTML- Seite nicht zu lang werden zu lassen, haben wir die kontnuierlichen Verteilungen
in zwei Kapitel unterteilt. Im vorliegenden Kapitel werden wir die Normalverteilung, die Exponentialverteilung
und die Gammaverteilung diskutieren, im nächsten Kapitel werden dann alle übrigen Verteilungen
behandelt.
Normalverteilung
Wir beginnen mit der Normalverteilung ![$N[a,\sigma ]$](img11.gif) in der allgemeinen
Form
in der allgemeinen
Form
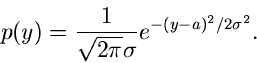 |
(1) |
Es genügt ersichtlich ein Algorithmus für die sogenannte Standard-
Normalverteilung ![$N[0,1]$](img25.gif) ,
,
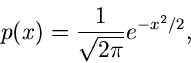 |
(2) |
da die Transformation
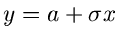 eine zufällige Veränderliche
der allgemeinen Normalverteilung ergibt. Die erzeugende Funktion der
Normalverteilung ist
eine zufällige Veränderliche
der allgemeinen Normalverteilung ergibt. Die erzeugende Funktion der
Normalverteilung ist
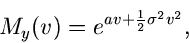 |
(3) |
sowie die logarithmisch erzeugende Funktion ist
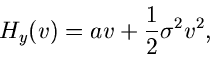 |
(4) |
mit den zwei Momenten
Wir hatten die Normalverteilung und ihre Eigenschaften im Verlaufe dieses
Kursus schon häufig diskutiert. Der breite Anwendungsbereich wird uns auch
noch in den folgenden Kapiteln begegnen.
Die wichtigste Eigenschaft der Normalverteilung folgt aus dem schon mehrfach
erwähnten zentralen Grenzwertsatz. Aus diesem Satz folgt, daß, wenn
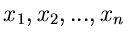 irgendwelche unabhängigen zufälligen
Veränderlichen sind, die Summe
irgendwelche unabhängigen zufälligen
Veränderlichen sind, die Summe
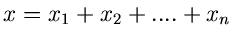 im Grenzfall
im Grenzfall
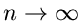 gegen eine Normalverteilung konvergiert. Auch für endliche
Werte von
gegen eine Normalverteilung konvergiert. Auch für endliche
Werte von  ist diese Behauptung schon sehr gut erfüllt. Aus dieser
Aussage folgt insbesondere, daß Meßfehler, die sich ja im allgemeinen
aus einer Vielzahl von unabhängigen statistischen und systematischen
Einzelfehlern additiv zusammenstzen, normalverteilt sind. Aus diesem Grunde
gibt man als Maß für einen Meßfehler die einfache Varianz
ist diese Behauptung schon sehr gut erfüllt. Aus dieser
Aussage folgt insbesondere, daß Meßfehler, die sich ja im allgemeinen
aus einer Vielzahl von unabhängigen statistischen und systematischen
Einzelfehlern additiv zusammenstzen, normalverteilt sind. Aus diesem Grunde
gibt man als Maß für einen Meßfehler die einfache Varianz 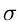 oder den zweifachen Wert
oder den zweifachen Wert 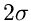 der Varianz an.
der Varianz an.
Methode der Randverteilungen.
Den Algorithmus mit Hilfe der Methode der Randverteilungen hatten wir bereits
ausführlich im vorigen Abschnitt diskutiert. Es genügt daher die folgende
Zusammenfassung: Erzeuge
![$u_{1},u_{2} \in U[0,1]$](img41.gif) , dann sind
, dann sind
zwei unabhängige normalverteilte Veränderliche aus ![$N[0,1]$](img25.gif) .
Die entsprechende Methode heißt haben wir in dem Applet mit JNormal1 bezeichnet.
.
Die entsprechende Methode heißt haben wir in dem Applet mit JNormal1 bezeichnet.
Verwerfungsmethode.
Ein sehr einfacher Algorithmus folgt aus der Verwerfungsmethode. Sei
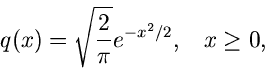 |
(7) |
die auf 1 normierte rechte Hälfte einer Standard- Normalverteilung. Da die
Normalverteilung ![$N[0,1]$](img25.gif) symmetrisch um Null ist, genügt es, eine
gemäß (7) erzeugte Veränderliche mit einem zufälligen Vorzeichen zu
versehen. Wir setzen
symmetrisch um Null ist, genügt es, eine
gemäß (7) erzeugte Veränderliche mit einem zufälligen Vorzeichen zu
versehen. Wir setzen
Die Funktion 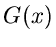 erreicht ihr Maximum
erreicht ihr Maximum 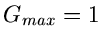 an der Stelle
an der Stelle 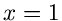 ,
die Dichtefunktion
,
die Dichtefunktion 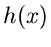 ist für
ist für 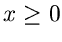 auf 1 normiert und
auf 1 normiert und 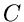 ist
ist
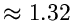 , also größer als 1. Einsetzen in den Ausdruck
, also größer als 1. Einsetzen in den Ausdruck
ergibt die Dichtefunktion (7). Alle Bedingungen der Verwerfungsmethode
sind also erfüllt. Die Erfolgswahrscheinlichkeit ist mit
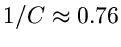 verhältnismäßig gut. Der Algorithmus lautet dann wie folgt: Erzeuge
verhältnismäßig gut. Der Algorithmus lautet dann wie folgt: Erzeuge
![$u_{1},u_{2},u_{3} \in U[0,1]$](img62.gif) und setze
und setze
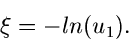 |
(9) |
Falls
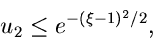 |
(10) |
akzeptiere 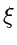 als Veränderliche, sonst beginne von vorne. Wenn
als Veränderliche, sonst beginne von vorne. Wenn
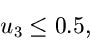 |
(11) |
ersetze 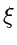 durch
durch 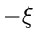 .
. 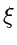 ist dann eine Veränderliche aus
ist dann eine Veränderliche aus ![$N[0,1]$](img25.gif) .
.
Die Bedingung (10) kann ersetzt werden durch
Mit dieser Feststellung kann man das Verfahren auch in der folgenden Form
formulieren: Erzeuge
![$v_{1},v_{2} \in E[1]$](img69.gif) und
und ![$u \in U[0,1]$](img70.gif) und
setze
und
setze
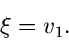 |
(12) |
Wenn dann
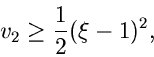 |
(13) |
akzeptiere 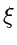 als Veränderliche, sonst beginne von vorne. Falls
als Veränderliche, sonst beginne von vorne. Falls
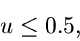 |
(14) |
ersetze 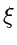 durch
durch 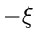 .
. 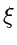 ist dann eine Veränderliche aus
ist dann eine Veränderliche aus ![$N[0,1]$](img25.gif) .
JNormal2 zeigt das Verfahren in der zweiten Formulierung an Hand
einer Unteroutine.
.
JNormal2 zeigt das Verfahren in der zweiten Formulierung an Hand
einer Unteroutine.
Approximation mit Hilfe des zentralen Grenzwertsatzes.
Wir hatten früher bereits festgestellt, daß die Summe
von  unabhängigen gleichverteilten Zufallszahlen aus dem Intervall
unabhängigen gleichverteilten Zufallszahlen aus dem Intervall
![$[-\frac{1}{2},\frac{1}{2}]$](img75.gif) im Grenzwert
im Grenzwert 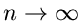 gegen eine
Normalverteilung mit Mittelwert
gegen eine
Normalverteilung mit Mittelwert 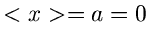 und Varianz
und Varianz
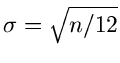 konvergiert. Wir hatten darüberhinaus festgestellt,
daß man bereits für
konvergiert. Wir hatten darüberhinaus festgestellt,
daß man bereits für 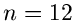 eine außerordentlich gute Approximation der
Normalverteilung mit
eine außerordentlich gute Approximation der
Normalverteilung mit 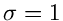 erhält. JNormal3 zeigt das Programm
für diesen speziellen Fall. Ersichtlich glänzt dieses Programm durch
seine Schlichtheit hinsichtlich mathematischer Operationen.
erhält. JNormal3 zeigt das Programm
für diesen speziellen Fall. Ersichtlich glänzt dieses Programm durch
seine Schlichtheit hinsichtlich mathematischer Operationen.
Eine weitere Approximation.
Durch numerisches Rechnen kann man sich leicht davon überzeugen, daß
für 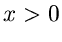 die Approximation
die Approximation
sehr gut erfüllt ist, sofern
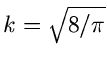 . Wir setzen also
. Wir setzen also
![\begin{displaymath}
\sqrt{\frac{2}{\pi}} e^{-x^{2}/2}
\approx \frac{2 k e^{-kx}...
...{-kx}]^{2}} = q(x),
\; \; \; x > 0, \; k=\sqrt{\frac{8}{\pi}}.
\end{displaymath}](img83.gif) |
(15) |
Die integrale Verteilungsfunktion für diese Approximation erhält man
am einfachsten mit der Substitution 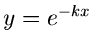 . Dieses führt auf
. Dieses führt auf
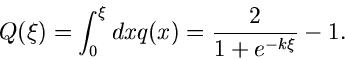 |
(16) |
Mit Hilfe der inversen Transformations- Methode muß die Gleichung
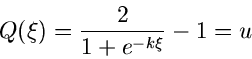 |
(17) |
mit ![$u \in U[0,1]$](img70.gif) nach
nach 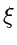 aufgelöst werden. Dieses ergibt
aufgelöst werden. Dieses ergibt
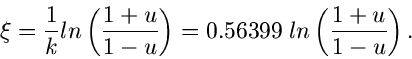 |
(18) |
Anschließend wird 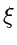 mit einem zufälligen Vorzeichen versehen.
Diesen Algorithmus zeigt JNormal4.
mit einem zufälligen Vorzeichen versehen.
Diesen Algorithmus zeigt JNormal4.
Die  -dimensionale Normalverteilung.
Die allgemeine
-dimensionale Normalverteilung.
Die allgemeine  - dimensionale Normalverteilung.
- dimensionale Normalverteilung.
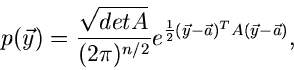 |
(19) |
kann mit Hilfe der Transformation
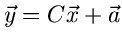 auf die
auf die
 - dimensionale unabhängige Standard- Normalverteilung
- dimensionale unabhängige Standard- Normalverteilung
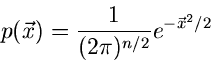 |
(20) |
transformiert werden. Es genügt also,  Veränderliche
Veränderliche
![$x_{1},x_{2},...,x_{n} \in N[0,1]$](img91.gif) zu erzeugen und zum Vektor
zu erzeugen und zum Vektor
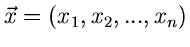 zusammenzufassen. Eine
Programmroutine ist in JNormalN1 gelistet. In dieser Routine verwenden
wir den Algorithmus JNormal1 zur Simulation einer einfachen normalverteilten
Veränderlichen. Dieser Teil kann natürlich durch jeden anderen
besprochenen Algorithmus ersetzt werden.
zusammenzufassen. Eine
Programmroutine ist in JNormalN1 gelistet. In dieser Routine verwenden
wir den Algorithmus JNormal1 zur Simulation einer einfachen normalverteilten
Veränderlichen. Dieser Teil kann natürlich durch jeden anderen
besprochenen Algorithmus ersetzt werden.
Die inverse 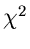 - Methode.
Bei dem soeben beschriebenen Verfahren muß
- Methode.
Bei dem soeben beschriebenen Verfahren muß  - mal eine eindimensionale
normalverteilte Veränderliche erzeugt werden. Wir diskutieren daher noch ein weiteres Verfahren,
das zwar vom logischen Aufbau komplizierter ist, aber mit wesentlich
weniger mathematischen Operationen auskommt. Wir erinnern in diesem
Zusammenhang an die Definition der
- mal eine eindimensionale
normalverteilte Veränderliche erzeugt werden. Wir diskutieren daher noch ein weiteres Verfahren,
das zwar vom logischen Aufbau komplizierter ist, aber mit wesentlich
weniger mathematischen Operationen auskommt. Wir erinnern in diesem
Zusammenhang an die Definition der 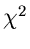 - Verteilung: Wenn
- Verteilung: Wenn
![$x_{1},x_{2},...,x_{n} \in N[0,1]$](img91.gif) , dann ist
die Größe
, dann ist
die Größe
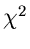 - verteilt mit
- verteilt mit  Freiheitsgraden,
Freiheitsgraden,
Diese Vorschrift kann umgekehrt werden. Dazu erzeugen wir zunächst eine
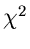 - verteilte Größe
- verteilte Größe ![$y \in Ch[n]$](img96.gif) . Einen hierzu geeigneten Algorithmus
JChi2 werden wir später diskutieren.
Die Größe
. Einen hierzu geeigneten Algorithmus
JChi2 werden wir später diskutieren.
Die Größe 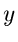 ist dann nichts anderes als das Quadrat des Radius
ist dann nichts anderes als das Quadrat des Radius 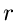 des
des  - dimensionalen Vektors
- dimensionalen Vektors
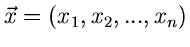 ,
,
Als nächstes erzeugen wir eine Gleichverteilung von Zufallszahlen auf der
Oberfläche der  - dimensionalen Einheitskugel. Diese bezeichnen wir
mit
- dimensionalen Einheitskugel. Diese bezeichnen wir
mit
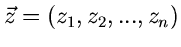 , sodaß also
, sodaß also
Den Vektor 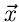 der Standard- Normalverteilung erhält man dann aus
der Standard- Normalverteilung erhält man dann aus
Das Verfahren zur Erzeugung einer Gleichverteilung von Zufallszahlen auf der
Oberfläche der Einheitskugel hatten wir im Prinzip bereits
behandelt, zumindest für den Fall 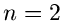 und
und 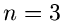 . Wir erzeugen
zunächst eine Gleichverteilung
. Wir erzeugen
zunächst eine Gleichverteilung
![$u_{1},u_{2},...,u_{n} \in U[-1,+1]$](img106.gif) im Volumen des
im Volumen des  - dimensionalen Quaders und verwerfen alle Punkte mit
- dimensionalen Quaders und verwerfen alle Punkte mit
Dieses liefert offensichtlich eine Gleichverteilung im Volumen der
 - dimensionalen Kugel. Die Normierung gemäß
- dimensionalen Kugel. Die Normierung gemäß
führt dann auf eine Gleichverteilung auf der Oberfläche der Kugel.
Das vollständige Verfahren lautet: Erzeuge
![$u_{1},u_{2},...,u_{n} \in U[-1,+1]$](img106.gif) und berechne
und berechne
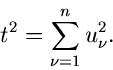 |
(21) |
Wenn
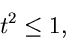 |
(22) |
akzeptiere 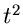 , sonst beginne von vorne. Berechne
, sonst beginne von vorne. Berechne
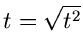 und
setze
und
setze
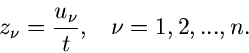 |
(23) |
Erzeuge ![$y \in Ch[n]$](img96.gif) , berechne
, berechne 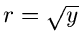 und setze
und setze
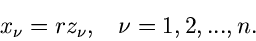 |
(24) |
Der zufällige Vektor
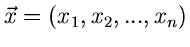 ist dann eine
Veränderliche der
ist dann eine
Veränderliche der  - dimensionalen unabhängigen Standard- Normalverteilung.
- dimensionalen unabhängigen Standard- Normalverteilung.
Das Programm zu diesem Verfahren ist in JNormalN2 gelistet. Die wesentlichen
mathematischen Operationen sind zwei Wurzelausdrücke und die Simulation der
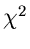 - verteilten Größe
- verteilten Größe 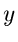 . Das Verfahren wäre außerordentlich
schnell, wenn nicht die Verwerfungsbedingung (22) enthalten wäre.
Die Erfolgswahrscheinlichkeit ist beschränkt auf
. Das Verfahren wäre außerordentlich
schnell, wenn nicht die Verwerfungsbedingung (22) enthalten wäre.
Die Erfolgswahrscheinlichkeit ist beschränkt auf
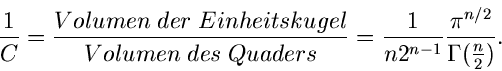 |
(25) |
Ersichtlich gilt für große  :
:
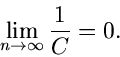 |
(26) |
Zum Beispiel ist für 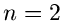 die Erfolgswahrscheinlichkeit
die Erfolgswahrscheinlichkeit
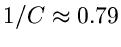 und für
und für 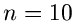 nur
nur
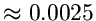 . Die Routine
JNormalN2 ist daher nur für Werte von
. Die Routine
JNormalN2 ist daher nur für Werte von  zwischen 2 und ungefähr 6
schneller als die Routine JNormalN1.
zwischen 2 und ungefähr 6
schneller als die Routine JNormalN1.
Lognormalverteilung.
Eine aus der allgemeinen Normalverteilung ![$N[a,\sigma ]$](img11.gif) durch die
Transformation
durch die
Transformation
hergeleitete Verteilung ist die Lognormalverteilung ![$LN[a,\sigma ]$](img14.gif) :
:
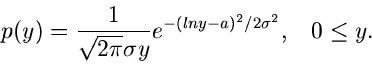 |
(27) |
Der übliche Algorithmus ist daher: Erzeuge ![$x \in N[0,1]$](img123.gif) und setze
und setze
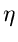 ist dann eine zufällige Veränderliche aus der Lognormalverteilung
ist dann eine zufällige Veränderliche aus der Lognormalverteilung
![$LN[a,\sigma ]$](img14.gif) (JLogNormal1).
(JLogNormal1).
Die Lognormalverteilung hat vielfache Anwendung in der Ökonomie bei der
Darstellung von Einnahmen und Ausgaben. Erwartungswert und Varianz sind durch
gegeben.
Exponentialverteilung
Zerfall quantenmechanischer Systeme.
Während die Normalverteilung eine zentrale Rolle im Rahmen der mathematischen
Statistik spielt, ist die Exponentialverteilung sicherlich die wichtigste
Verteilung der mikroskopischen Physik, in der Physik also, die mit Hilfe
der Quantenmechanik beschrieben werden muß. Ein in Ruhe befindliches
instabiles quantenmechanisches System (Atom, Kern, Teilchen) wird mit Hilfe
der Wellenfunktion
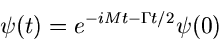 |
(28) |
beschrieben, wobei 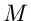 die Masse,
die Masse,
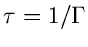 die mittlere Lebensdauer
und
die mittlere Lebensdauer
und 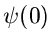 die Wellenfunktion am Zeitpunkt
die Wellenfunktion am Zeitpunkt 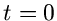 ist. Die Größe
ist. Die Größe
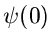 beschreibt alle anderen, nicht von der Zeit abhängenden Größen
des Systems. Die Wahrscheinlichkeit dafür, daß wir das System am Zeitpunkt
beschreibt alle anderen, nicht von der Zeit abhängenden Größen
des Systems. Die Wahrscheinlichkeit dafür, daß wir das System am Zeitpunkt
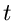 noch unverändert antreffen, ist nach den Grundaxiomen der Quantenmechanik
durch
noch unverändert antreffen, ist nach den Grundaxiomen der Quantenmechanik
durch
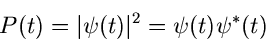 |
(29) |
gegeben. Einsetzen von 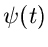 aus (28) ergibt
aus (28) ergibt
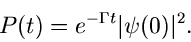 |
(30) |
Wir sehen also, daß die Zerfallswahrscheinlichkeit eines instabilen
quantenmechanisches Systems einer Exponentialverteilung gehorcht.
Die normierte allgemeine Exponentialverteilung
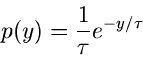 |
(31) |
erhält man aus der Standard- Normalverteilung
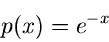 |
(32) |
mit Hilfe der Transformation 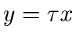 . Wir bezeichnen die
Exponentialverteilung mit dem mnemotechnischen Symbol
. Wir bezeichnen die
Exponentialverteilung mit dem mnemotechnischen Symbol ![$E[\tau]$](img17.gif) . Die
erzeugenden und logarithmisch erzeugenden Funktionen sind
. Die
erzeugenden und logarithmisch erzeugenden Funktionen sind
Aus der Reihenentwicklung der logarithmisch erzeugenden Funktion,
folgen sofort die Ausdrücke für Erwartungswert und Varianz:
Inverse Transformationsmethode.
Zur Simulation einer Veränderlichen der Standard- Exponentialverteilung
![$E[1]$](img148.gif) verwendet man fast immer die inverse Transformationsmethode. Das
Verfahren wurde bereits ausgiebig diskutiert. Wir können daher den
Algorithmus sofort anschreiben: Erzeuge
verwendet man fast immer die inverse Transformationsmethode. Das
Verfahren wurde bereits ausgiebig diskutiert. Wir können daher den
Algorithmus sofort anschreiben: Erzeuge ![$u \in U[0,1]$](img70.gif) und setze
und setze
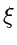 ist dann eine Veränderliche aus
ist dann eine Veränderliche aus ![$E[1]$](img148.gif) . Die Programmroutine
JExponential ist trivial und braucht nicht weiter erläutert zu werden.
. Die Programmroutine
JExponential ist trivial und braucht nicht weiter erläutert zu werden.
Obwohl dieser Algorithmus bestechend einfach ist, sind vielfältige andere
Algorithmen entwickelt worden, u.a. mit Hilfe der Composition- Methode,
der Verwerfungsmethode und der Forsythe- Methode.
Allen diesen Algorithmen gemeinsam ist, daß sie die Berechnung der
Logarithmus- Funktion vermeiden, dafür aber logische Operationen einführen
müssen. Diese Verfahren sind auf den heute zur Verfügung stehenden
Rechnern im Vergleich zu JExponential nicht empfehlenswert, wir haben daher auf eine
weitere Diskussion verzichtet. Die ersten 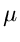 - Prozessoren dagegen, wie zum
Beispiel der legendäre INTEL 8080, waren nur für logische Operationen
und einfache arithmetische Algebra ausgelegt. Hier waren andere Verfahren
durchaus von Wert.
- Prozessoren dagegen, wie zum
Beispiel der legendäre INTEL 8080, waren nur für logische Operationen
und einfache arithmetische Algebra ausgelegt. Hier waren andere Verfahren
durchaus von Wert.
n-dimensionale unabhängige Exponentialverteilung.
Die Simulation der allgemeinen n- dimensionalen Standard- Exponentialverteilung
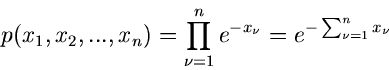 |
(37) |
erfordert die Berechnung von  Logarithmus- Funktionen,
Logarithmus- Funktionen,
mit
![$u_{1},u_{2},...,u_{n} \in U[0,1]$](img153.gif) . Für gewisse Werte von
. Für gewisse Werte von  kann
hierfür ein schnellerer Algorithmus angewendet werden, den wir im folgenden
herleiten. Das Verfahren beruht auf einer Reduktionsmethode mit nachfolgender
Variablen- Transformation.
kann
hierfür ein schnellerer Algorithmus angewendet werden, den wir im folgenden
herleiten. Das Verfahren beruht auf einer Reduktionsmethode mit nachfolgender
Variablen- Transformation.
Wir erzeugen zunächst  gleichverteilte Zufallszahlen
gleichverteilte Zufallszahlen
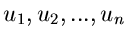 und bilden
und bilden
Wir behaupten jetzt, daß 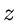 durch die sogenannte Erlang- Verteilung
durch die sogenannte Erlang- Verteilung
![$Er[n,1]$](img157.gif) ,
,
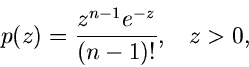 |
(38) |
beschrieben wird. Zum Beweis bemerken wir, daß die logarithmisch erzeugende
Funktion der Summe von  Veränderlichen
Veränderlichen
der Exponentialfunktion
durch
gegeben ist. Auf Grund der Ergebnisse in Kap.3 ist dieses die
logarithmisch erzeugende Funktion von
Da die
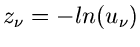 exponentiell verteilt sind, falls
exponentiell verteilt sind, falls
![$u_{\nu} \in U[0,1]$](img164.gif) , folgt unsere Behauptung, daß
, folgt unsere Behauptung, daß
Als nächstes erzeugen wir weitere 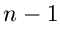 Zufallszahlen
Zufallszahlen
![$u_{n+1},u_{n+2},...,u_{2n-1} \in U[0,1]$](img167.gif) und sortieren diese in aufsteigender
Reihenfolge. Diese letzteren Zahlen bezeichnen wir mit
und sortieren diese in aufsteigender
Reihenfolge. Diese letzteren Zahlen bezeichnen wir mit
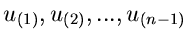 . Weiterhin setzen wir
. Weiterhin setzen wir 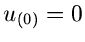 und
und
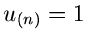 . Dann gilt also:
. Dann gilt also:
Wir setzen
Wie man zeigen kann (siehe geordntete Statistik in Kap.3), ist der 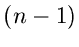 - dimensionale
Vektor
- dimensionale
Vektor
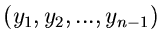 gemäß der Dichtefunktion
gemäß der Dichtefunktion
verteilt. Da die Zufallszahlen
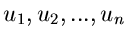 unabhängig von den
unabhängig von den
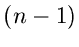 Zufallszahlen
Zufallszahlen
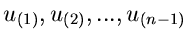 sind, so ist auch
sind, so ist auch
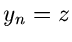 unabhängig von den Veränderlichen
unabhängig von den Veränderlichen
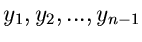 .
Daher ist die gemeinsame Dichtefunktion des Vektors
.
Daher ist die gemeinsame Dichtefunktion des Vektors
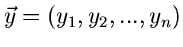 als Produkt darstellbar:
als Produkt darstellbar:
Mit Hilfe der Transformation
erhalten wir schließlich
also die einfache  - dimensionale unabhängige Standard-
Exponentialverteilung.
- dimensionale unabhängige Standard-
Exponentialverteilung.
Zusammengefaßt erhalten wir folgenden Algorithmus: Erzeuge
![$u_{1},u_{2},...,u_{n} \in U[0,1]$](img153.gif) und bilde
und bilde
Erzeuge weitere 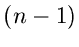 Zufallszahlen
Zufallszahlen
![$u_{n+1},u_{n+2},...,u_{2n-1} \in U[0,1]$](img167.gif) ,
sortiere diese in aufsteigender Reihenfolge und bezeichne diese mit
,
sortiere diese in aufsteigender Reihenfolge und bezeichne diese mit
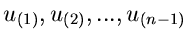 . Setze außerdem
. Setze außerdem 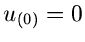 und
und
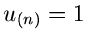 . Bilde
. Bilde
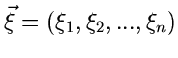 ist dann ein Vektor der
unabhängigen
ist dann ein Vektor der
unabhängigen  - dimensionalen Standard- Exponentialverteilung
- dimensionalen Standard- Exponentialverteilung
![$E[1,1,...,1]$](img184.gif) .
.
Ersichtlich muß in diesem Verfahren nur einmal der Logarithmus berechnet
werden, im Gegensatz zu  Logarithmus- Berechnungen bei der inversen
Transformationsmethode. Demgegenüber stehen doppelt so viele Aufrufe des
Zufallszahlen- Generators und eine zusätzliche Sortierung von
Logarithmus- Berechnungen bei der inversen
Transformationsmethode. Demgegenüber stehen doppelt so viele Aufrufe des
Zufallszahlen- Generators und eine zusätzliche Sortierung von 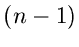 Zahlen. Der letztere Algorithmus erweist sich daher nur für Werte von
Zahlen. Der letztere Algorithmus erweist sich daher nur für Werte von
 zwischen etwa 3 und 6 der inversen Transformationsmethode überlegen.
Programmroutinen sind in JExponentialN1 und JExponentialN2 gelistet.
zwischen etwa 3 und 6 der inversen Transformationsmethode überlegen.
Programmroutinen sind in JExponentialN1 und JExponentialN2 gelistet.
Gammaverteilung
Vorbemerkung.
Die Verallgemeinerung der Exponentialverteilung und der bereits im vorherigen
Abschnitt behandelten Erlang- Verteilung ist die Gammaverteilung
![$G[\alpha, \beta]$](img20.gif) ,
,
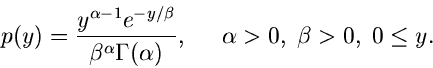 |
(39) |
Ersichtlich genügt es, Algorithmen zur Simulation der Standard- Gammaverteilung
![$G[\alpha, 1]$](img186.gif) ,
,
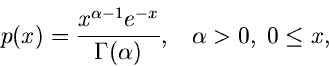 |
(40) |
zu diskutieren, da die Transformation 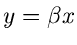 eine Veränderliche der
allgemeinen Gammaverteilung liefert. Wie bereits diskutiert, erhalten wir
für
eine Veränderliche der
allgemeinen Gammaverteilung liefert. Wie bereits diskutiert, erhalten wir
für 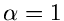 die Exponentialverteilung
die Exponentialverteilung ![$E[\beta]$](img190.gif) und für
ganzzahliges
und für
ganzzahliges 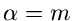 die Erlang- Verteilung
die Erlang- Verteilung ![$Er[m,\beta]$](img23.gif) . Die
erzeugende Funktion der Gammverteilung ist
. Die
erzeugende Funktion der Gammverteilung ist
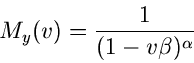 |
(41) |
und die logarithmisch erzeugende Funktion ist
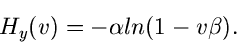 |
(42) |
Erwartungswert und Varianz erhält man am einfachsten aus der Reihenentwicklung
der logarithmisch erzeugenden Funktion
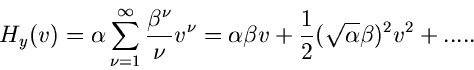 |
(43) |
zu
Reproduktivität der Gammaverteilung.
Die wichtigste Eigenschaft der Gammaverteilung ist ihre Reproduktivität:
Seien 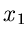 und
und 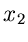 zwei Veränderliche aus Gammaverteilungen mit
Parametern
zwei Veränderliche aus Gammaverteilungen mit
Parametern 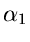 und
und 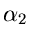 , d.h.
, d.h.
![$x_{1} \in G[\alpha_{1},\beta]$](img201.gif) und
und
![$x_{2} \in G[\alpha_{2},\beta]$](img202.gif) . Dann ist
. Dann ist 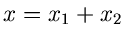 eine
Veränderliche aus der Gammaverteilung
eine
Veränderliche aus der Gammaverteilung
![$G[\alpha_{1}+\alpha_{2}, \beta]$](img204.gif) .
Der Beweis ist einfach und erfolgt über die logarithmisch erzeugende
Funktion.
.
Der Beweis ist einfach und erfolgt über die logarithmisch erzeugende
Funktion.
sind die logarithmisch erzeugenden Funktionen von
Nach Kap.3 ist dann, da 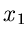 und
und 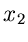 unabhängig voneinander sind,
unabhängig voneinander sind,
die logarithmisch erzeugende Funktion der Summe 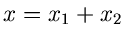 der
zwei Veränderlichen
der
zwei Veränderlichen 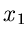 und
und 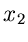 . Hieraus folgt sofort unsere
Behauptung. Wichtig ist offensichtlich, daß der Parameter
. Hieraus folgt sofort unsere
Behauptung. Wichtig ist offensichtlich, daß der Parameter 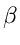 in
beiden Verteilungen identisch ist.
in
beiden Verteilungen identisch ist.
Die Verallgemeinerung auf  Veränderliche
Veränderliche
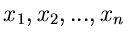 aus den
Gammaverteilungen
aus den
Gammaverteilungen
![$G[\alpha_{1},\beta]$](img215.gif) ,
,
![$G[\alpha_{2}, \beta]$](img216.gif) , ....,
, ....,
![$G[\alpha_{n}, \beta]$](img217.gif) ist trivial und ergibt, daß die Veränderliche
ist trivial und ergibt, daß die Veränderliche
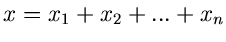 aus
aus
![$G[\alpha_{1}+\alpha_{2}+...+ \alpha_{n}, \beta]$](img219.gif) ist.
ist.
Reproduktivitäts- Verfahren.
Ein auf der Reproduktivitätseigenschaft basierendes Verfahren soll im folgenden
vorgestellt werden. Wir setzen
wobei
und erzeugen 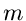 Zufallszahlen
Zufallszahlen
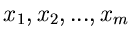 aus der
Exponentialverteilung
aus der
Exponentialverteilung ![$E[1]$](img148.gif) ,
,
sowie eine Zufallszahl 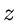 aus der speziellen Gammaverteilung
aus der speziellen Gammaverteilung ![$G[\delta,1]$](img229.gif) ,
,
mit
Auf Grund der Reproduktivität ist dann
eine Veränderliche der Standard- Gammaverteilung ![$G[\alpha, 1]$](img186.gif)
Die Simulation der speziellen Gammaverteilung ![$G[\delta,1]$](img229.gif) mit
mit
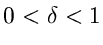 kann wie folgt durchgeführt werden.
kann wie folgt durchgeführt werden.
Hierzu führen wir noch die Betaverteilung
![$B[\alpha, \beta]$](img235.gif) ein.
Diese ist allgemein definiert durch
ein.
Diese ist allgemein definiert durch
Wir benötigen im folgenden die spezielle Betaverteilung
![$B[\delta, 1-\delta]$](img237.gif) ,
,
Wegen 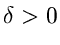 und
und 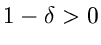 ist diese Verteilung ersichtlich nur
für
ist diese Verteilung ersichtlich nur
für
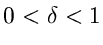 definiert. Seien also
definiert. Seien also
![$w \in B[\delta,1-\delta]$](img241.gif) und
und
![$v \in E[1]$](img242.gif) , dann erhalten wir mit Hilfe einer Variablen- Transformation
für die Veränderlichen
, dann erhalten wir mit Hilfe einer Variablen- Transformation
für die Veränderlichen
die Dichtefunktion
Die Randverteilung in 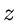 ist
ist
Dieses ist offensichtlich die gesuchte Gammaverteilung ![$G[\delta,1]$](img229.gif) .
.
Wir fassen das Verfahren zusammen: Setze
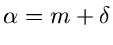 mit
mit
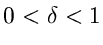 . Erzeuge
. Erzeuge
![$u_{1},u_{2},...,u_{m} \in U[0,1]$](img250.gif) und bilde
und bilde
Erzeuge
![$w \in B[\delta,1-\delta]$](img241.gif) und
und ![$v \in E[1]$](img242.gif) . Die Veränderliche
. Die Veränderliche
ist dann eine Veränderliche aus ![$G[\alpha, 1]$](img186.gif) mit
mit
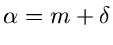 ,
,
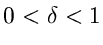 . Das Programmlisting JGamma2 im zweiten
Applet dieses
Kapitels zeigt diesen
Algorithmus. JGamma1 zeigt den einfachen Programmcode für
ganzzahliges
. Das Programmlisting JGamma2 im zweiten
Applet dieses
Kapitels zeigt diesen
Algorithmus. JGamma1 zeigt den einfachen Programmcode für
ganzzahliges 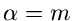 . Diese Routine haben wir auch unter dem Namen
JErlang1 hinzugefügt..
. Diese Routine haben wir auch unter dem Namen
JErlang1 hinzugefügt..
Das soeben diskutierte Verfahren erfordert im wesentlichen die Erzeugung
einer Veränderlichen aus der Betaverteilung. Wie wir im nächsten Abschnitt
sehen werden, kann dieses zu erheblichem Rechenzeit- Bedarf führen.
Günstiger sind daher im allgemeinen Methoden, die auf dem
Verwerfungsverfahren beruhen.
Approximation für große 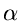 .
Für große Werte von
.
Für große Werte von 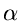 bzw
bzw 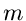 kann die Erlang- Verteilung
kann die Erlang- Verteilung ![$Er[m,1]$](img254.gif) durch eine Normalverteilung ersetzt werden. Dieses folgt aus der Tatsache,
daß eine Veränderliche der Erlang- Verteilung als Summe von
durch eine Normalverteilung ersetzt werden. Dieses folgt aus der Tatsache,
daß eine Veränderliche der Erlang- Verteilung als Summe von 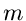 Veränderlichen der Exponentialverteilung
Veränderlichen der Exponentialverteilung ![$E[1]$](img148.gif) geschrieben werden kann.
Erwartungswert und Varianz der Erlang- Verteilung sind
für große Werte von
geschrieben werden kann.
Erwartungswert und Varianz der Erlang- Verteilung sind
für große Werte von 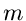 durch
durch
gegeben. Die Approximation kann also geschrieben werden als
Der Algorithmus lautet: Erzeuge ![$v \in N[0,1]$](img260.gif) , dann ist
, dann ist
eine Veränderliche der Erlang- Verteilung ![$Er[m,1]$](img254.gif) für große
für große 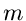 (
(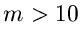 ). Diese Routine ist unter dem Namen JErlang2
gelistet.
). Diese Routine ist unter dem Namen JErlang2
gelistet.
1. Verwerfungsverfahren.
Als erstes betrachten wir ein Verfahren, in dem die Simulation der speziellen
Gammaverteilung
mit Hilfe eines Verwerfungsverfahrens durchgeführt wird. Der Algorithmus
hierzu wurde bereits ausführlich diskutiert.
Wir fassen das Verfahren noch einmal in einer mathematisch etwas abgewandelten
Formulierung zusammen:
1. Berechne 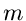 und
und 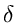 gemäß
gemäß
2. Erzeuge
![$u_{1},u_{2},...,u_{m} \in U[0,1]$](img250.gif) und setze
und setze
Erzeuge
![$u_{m+1},u_{m+2} \in U[0,1]$](img267.gif) und berechne
und berechne
Wenn 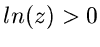 , fahre fort bei Punkt 3. Ansonsten berechne
, fahre fort bei Punkt 3. Ansonsten berechne 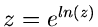 .
Falls
.
Falls
akzeptiere 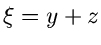 als Veränderliche der Gammaverteilung
als Veränderliche der Gammaverteilung ![$G[\alpha, 1]$](img186.gif) ,
sonst wiederhole von Punkt 2.
,
sonst wiederhole von Punkt 2.
3. Setze
Wenn
akzeptiere 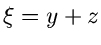 als Veränderliche der Gammaverteilung
als Veränderliche der Gammaverteilung ![$G[\alpha, 1]$](img186.gif) ,
sonst wiederhole bei Punkt 2. JGamma3 zeigt den Programm- Code.
,
sonst wiederhole bei Punkt 2. JGamma3 zeigt den Programm- Code.
2. Verwerfungsverfahren.
Das zweite Verwerfungsverfahren beruht auf dem gleichen mathematischen
Formalismus wie die Routine JGam2, nur daß jetzt die Simulation der
Betaverteilung durch ein anderes Verwerfungsverfahren ersetzt wird. Die
Funktionen
wobei, wie bisher,
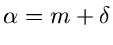 ,
,
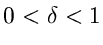 , erfüllen ersichtlich
die Bedingungen der Verwerfungsmethode.
Die Simulation der Dichtefunktion
, erfüllen ersichtlich
die Bedingungen der Verwerfungsmethode.
Die Simulation der Dichtefunktion 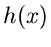 ist einfach und beruht auf der
alternativen Simulation zweier Erlang- Verteilungen
ist einfach und beruht auf der
alternativen Simulation zweier Erlang- Verteilungen ![$Er[m-1,1]$](img281.gif) und
und
![$Er[m,1]$](img254.gif) mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit 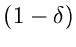 bzw
bzw 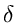 . Die
Erfolgswahrscheinlickeit
. Die
Erfolgswahrscheinlickeit 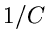 konvergiert für große Werte von
konvergiert für große Werte von 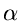 bzw
bzw 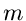 gegen 1:
gegen 1:
Wegen
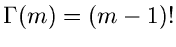 für ganzzahliges positives
für ganzzahliges positives 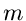 ist für
ist für 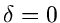 die
Erfolgswahrscheinlichkeit immer gleich 1.
Der Algorithmus lautet:
die
Erfolgswahrscheinlichkeit immer gleich 1.
Der Algorithmus lautet:
1. Berechne 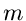 und
und 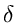 gemäß
gemäß
2. Erzeuge
![$u_{1},u_{2},...,u_{m},u_{m+1},u_{m+2},u_{m+3} \in U[0,1]$](img287.gif) und setze
und setze
Falls
akzeptiere 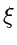 als Veränderliche der Gammaverteilung
als Veränderliche der Gammaverteilung ![$G[\alpha, 1]$](img186.gif) ,
sonst beginne bei Punkt 2. JGamma4 zeigt den Programmcode.
,
sonst beginne bei Punkt 2. JGamma4 zeigt den Programmcode.
3. Verwerfungsverfahren.
Ein drittes Verwerfungsverfahren beruht auf den Festsetzungen
und ist nur anwendbar für 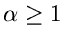 . Die Erfolgswahrscheinlichkeit
. Die Erfolgswahrscheinlichkeit
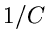 kann für große
kann für große 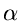 durch
durch
approximiert werden. Der Algorithmus lautet: Erzeuge
![$u_{1},u_{2} \in U[0,1]$](img41.gif) und berechne
und berechne
Wenn
akzeptiere 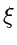 als Veränderliche von
als Veränderliche von ![$G[\alpha, 1]$](img186.gif) , sonst beginne von vorne.
Hierbei haben wir, wie auch schon in vielen vorherigen Beispielen,
die komplizierte Funktion
, sonst beginne von vorne.
Hierbei haben wir, wie auch schon in vielen vorherigen Beispielen,
die komplizierte Funktion 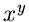 dadurch vermieden, daß auf beiden Seiten
der Verwerfungsabfrage der Logarithmus gebildet wurde. Auf den meisten
Rechnern ist der Logarithmus
dadurch vermieden, daß auf beiden Seiten
der Verwerfungsabfrage der Logarithmus gebildet wurde. Auf den meisten
Rechnern ist der Logarithmus 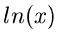 und die Exponentialfunktion
und die Exponentialfunktion 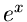 eine Standard- Routine, während ein Ausdruck der Form
eine Standard- Routine, während ein Ausdruck der Form 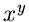 mit Hilfe der
Umformung
mit Hilfe der
Umformung
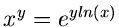 berechnet wird, also aus zwei Operationen
besteht. Die Routine JGamma5 zeigt den Algorithmus.
berechnet wird, also aus zwei Operationen
besteht. Die Routine JGamma5 zeigt den Algorithmus.
4. Verwerfungsverfahren.
Die nächste Prozedur faktorisiert 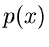 in der Form
in der Form
mit
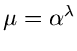 und
und
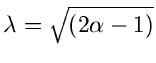 .
Die Erfolgswahrscheinlichkeit ist mit
.
Die Erfolgswahrscheinlichkeit ist mit
für alle Werte von 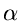 relativ gut. Die Simulation der Dichtefunktion
relativ gut. Die Simulation der Dichtefunktion
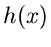 beruht auf der inversen Transformationsmethode. Wir transformieren
gemäß
beruht auf der inversen Transformationsmethode. Wir transformieren
gemäß
und erhalten die Dichtefunktion der Veränderlichen 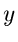 zu
zu
Die integrale Verteilungsfunktion ist
Mit
![$u_{1},u_{2} \in U[0,1]$](img41.gif) ergeben sich die Gleichungen
ergeben sich die Gleichungen
sowie die Ungleichung
Die letzte Ungleichung zur Verwerfungsabfrage kann vereinfacht werden zu
mit
Damit ergibt sich der Algorithmus: 1. Berechne in einer
Initialisierungsroutine die Größen
2. Erzeuge
![$u_{1},u_{2} \in U[0,1]$](img41.gif) und setze
und setze
Wenn
akzeptiere 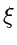 als Veränderliche von
als Veränderliche von ![$G[\alpha, 1]$](img186.gif) , sonst beginne von
vorne bei Punkt 2. JGamma6 zeigt das Programmlisting, das aus einem
Initialisierungsteil und dem Generator selbst besteht.
, sonst beginne von
vorne bei Punkt 2. JGamma6 zeigt das Programmlisting, das aus einem
Initialisierungsteil und dem Generator selbst besteht.
5. Verwerfungsverfahren.
Ein weiteres Verwerfungsverfahren arbeitet mit Hilfe der Cauchy- Verteilung
![$C[\gamma, \lambda]$](img331.gif) ,
,
Diese Verteilung ist allgemein auf der gesamten reellen Achse definiert.
Bei Einschränkung des Definitionsbereiches auf 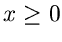 muß die Normierung
geändert werden. Man erhält
muß die Normierung
geändert werden. Man erhält
wobei
die integrale Verteilungsfunktion der Cauchy- Verteilung ist. Mit Hilfe der
inversen Transformationsmethode ergibt sich, daß
eine Veränderliche von 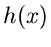 ist, wobei, wie immer,
ist, wobei, wie immer,
![$u_{1} \in U[0,1]$](img336.gif) .
Das Verwerfungsverfahren für die Gammaverteilung
.
Das Verwerfungsverfahren für die Gammaverteilung ![$G[\alpha, 1]$](img186.gif) erhält man
mit den weiteren Festsetzungen
erhält man
mit den weiteren Festsetzungen
mit
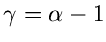 und
und
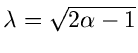 .
Der Algorithmus lautet: 1. Berechne in einem externen Programm
.
Der Algorithmus lautet: 1. Berechne in einem externen Programm
2. Erzeuge
![$u_{1},u_{2} \in U[0,1]$](img41.gif) und setze
und setze
Wenn
akzeptiere 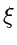 als Veränderliche von
als Veränderliche von ![$G[\alpha, 1]$](img186.gif) , sonst beginne von
vorne bei Punkt 2.
Die entsprechende Routine ist JGamma7.
, sonst beginne von
vorne bei Punkt 2.
Die entsprechende Routine ist JGamma7.
6. Verwerfungsverfahren.
Ein Verwerfungsverfahren für die Gammaverteilung
![$G[\alpha, \beta]$](img20.gif) mit
mit
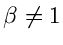 ist das folgende:
ist das folgende:
mit
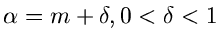 . Ersichtlich kann die Faktorisierung
für
. Ersichtlich kann die Faktorisierung
für 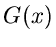 und
und 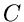 nur für
nur für 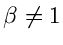 durchgeführt werden. Das
Verfahren ist ähnlich dem 3. Verwerfungsverfahren, nur daß jetzt die
Gammaverteilung
durchgeführt werden. Das
Verfahren ist ähnlich dem 3. Verwerfungsverfahren, nur daß jetzt die
Gammaverteilung
![$G[\alpha, \beta]$](img20.gif) durch die allgemeine Erlang- Verteilung
durch die allgemeine Erlang- Verteilung
![$Er[m,\beta]$](img23.gif) approximiert wird, anstatt durch die Exponentialverteilung
approximiert wird, anstatt durch die Exponentialverteilung
![$E[\alpha]$](img353.gif) im 3. Verwerfungsverfahren. Die Mathematik dieses Verfahrens
ist sehr einfach, sodaß wir den Algorithmus sofort hinschreiben können:
1. Berechne
im 3. Verwerfungsverfahren. Die Mathematik dieses Verfahrens
ist sehr einfach, sodaß wir den Algorithmus sofort hinschreiben können:
1. Berechne 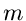 und
und 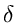 aus
aus
und setze
2. Erzeuge
![$u_{1},u_{2},...,u_{m} \in U[0,1]$](img250.gif) und setze
und setze
Wenn
akzeptiere 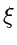 als Veränderliche von
als Veränderliche von
![$G[\alpha, \beta]$](img20.gif) , sonst beginne
von vorne bei Punkt 2. Das Programm ist in JGamma8 gelistet.
, sonst beginne
von vorne bei Punkt 2. Das Programm ist in JGamma8 gelistet.
Wir haben die Gamma- Verteilung benutzt, um die vielfältigen Methoden aufzuzeigen.
Die Rechenzeiten für die einzelnen Methoden sind zwar nicht dramatisch verschieden, aber
natürlich schon etwas unterschiedlich. Im nächsten Abschnitt werden wir die Simulation weiterer
kontinuierlicher Verteilungen besprechen.
Harm Fesefeldt
2006-07-11
![]() bis
bis ![]() mit
mit
![]() kennzeichnen. Eine normalverteilte Veränderliche
entsprechend mit
kennzeichnen. Eine normalverteilte Veränderliche
entsprechend mit
![]() . Die Dichtefunktion bzw
Wahrscheinlichkeitsverteilung wird dabei mit einem mnemotechnisch einfachen
Symbol (
. Die Dichtefunktion bzw
Wahrscheinlichkeitsverteilung wird dabei mit einem mnemotechnisch einfachen
Symbol (![]() = uniform,
= uniform, ![]() = normal) gekennzeichnet, die Parameter der
Verteilung in eckigen Klammern angefügt. Eine Zusammenstellung der wichtigsten
kontinuierlichen Verteilungen und ihrer Symbole ist in Tabelle 1 gelistet.
Für die folgenden Erörterungen verweisen wir auf das erste
Applet dieses Kapitels.
= normal) gekennzeichnet, die Parameter der
Verteilung in eckigen Klammern angefügt. Eine Zusammenstellung der wichtigsten
kontinuierlichen Verteilungen und ihrer Symbole ist in Tabelle 1 gelistet.
Für die folgenden Erörterungen verweisen wir auf das erste
Applet dieses Kapitels.
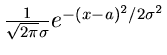
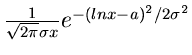
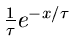
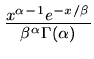
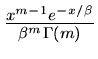
![]() in der allgemeinen
Form
in der allgemeinen
Form
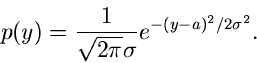
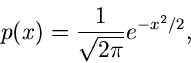
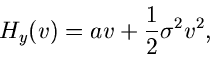
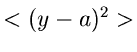
![]() irgendwelche unabhängigen zufälligen
Veränderlichen sind, die Summe
irgendwelche unabhängigen zufälligen
Veränderlichen sind, die Summe
![]() im Grenzfall
im Grenzfall
![]() gegen eine Normalverteilung konvergiert. Auch für endliche
Werte von
gegen eine Normalverteilung konvergiert. Auch für endliche
Werte von ![]() ist diese Behauptung schon sehr gut erfüllt. Aus dieser
Aussage folgt insbesondere, daß Meßfehler, die sich ja im allgemeinen
aus einer Vielzahl von unabhängigen statistischen und systematischen
Einzelfehlern additiv zusammenstzen, normalverteilt sind. Aus diesem Grunde
gibt man als Maß für einen Meßfehler die einfache Varianz
ist diese Behauptung schon sehr gut erfüllt. Aus dieser
Aussage folgt insbesondere, daß Meßfehler, die sich ja im allgemeinen
aus einer Vielzahl von unabhängigen statistischen und systematischen
Einzelfehlern additiv zusammenstzen, normalverteilt sind. Aus diesem Grunde
gibt man als Maß für einen Meßfehler die einfache Varianz ![]() oder den zweifachen Wert
oder den zweifachen Wert ![]() der Varianz an.
der Varianz an.
![]() , dann sind
, dann sind
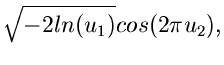
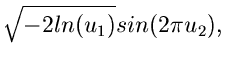
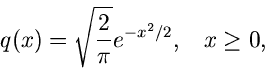
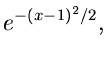
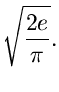
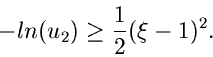
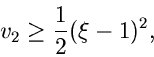
![$[-\frac{1}{2},\frac{1}{2}]$](img75.gif) im Grenzwert
im Grenzwert 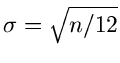 konvergiert. Wir hatten darüberhinaus festgestellt,
daß man bereits für
konvergiert. Wir hatten darüberhinaus festgestellt,
daß man bereits für ![]() die Approximation
die Approximation
![\begin{displaymath}
e^{-x^{2}/2} \approx \frac{4 e^{-kx}}{[1+e^{-kx}]^{2}}
\end{displaymath}](img81.gif)
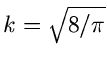 . Wir setzen also
. Wir setzen also
![\begin{displaymath}
\sqrt{\frac{2}{\pi}} e^{-x^{2}/2}
\approx \frac{2 k e^{-kx}...
...{-kx}]^{2}} = q(x),
\; \; \; x > 0, \; k=\sqrt{\frac{8}{\pi}}.
\end{displaymath}](img83.gif)
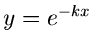 . Dieses führt auf
. Dieses führt auf
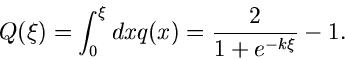
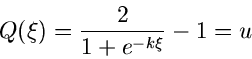
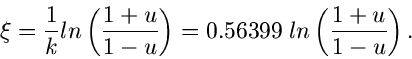
![]() -dimensionale Normalverteilung.
Die allgemeine
-dimensionale Normalverteilung.
Die allgemeine ![]() - dimensionale Normalverteilung.
- dimensionale Normalverteilung.
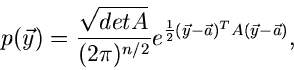
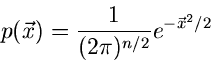
![]() - Methode.
Bei dem soeben beschriebenen Verfahren muß
- Methode.
Bei dem soeben beschriebenen Verfahren muß ![]() - mal eine eindimensionale
normalverteilte Veränderliche erzeugt werden. Wir diskutieren daher noch ein weiteres Verfahren,
das zwar vom logischen Aufbau komplizierter ist, aber mit wesentlich
weniger mathematischen Operationen auskommt. Wir erinnern in diesem
Zusammenhang an die Definition der
- mal eine eindimensionale
normalverteilte Veränderliche erzeugt werden. Wir diskutieren daher noch ein weiteres Verfahren,
das zwar vom logischen Aufbau komplizierter ist, aber mit wesentlich
weniger mathematischen Operationen auskommt. Wir erinnern in diesem
Zusammenhang an die Definition der ![]() - Verteilung: Wenn
- Verteilung: Wenn
![]() , dann ist
die Größe
, dann ist
die Größe
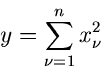
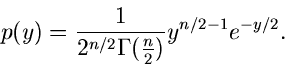
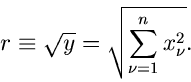
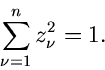
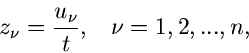
![]() und berechne
und berechne
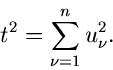
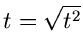 und
setze
und
setze
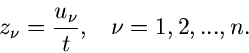
![]() - verteilten Größe
- verteilten Größe ![]() . Das Verfahren wäre außerordentlich
schnell, wenn nicht die Verwerfungsbedingung (22) enthalten wäre.
Die Erfolgswahrscheinlichkeit ist beschränkt auf
. Das Verfahren wäre außerordentlich
schnell, wenn nicht die Verwerfungsbedingung (22) enthalten wäre.
Die Erfolgswahrscheinlichkeit ist beschränkt auf
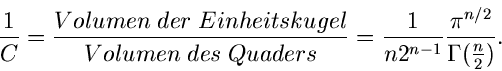
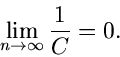
![]() durch die
Transformation
durch die
Transformation
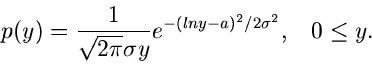
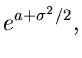
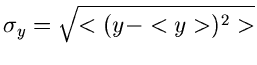
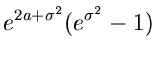
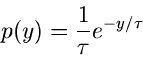
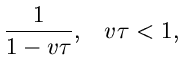
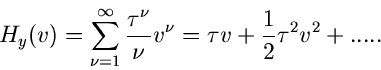
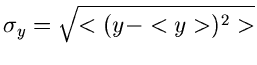
![]() verwendet man fast immer die inverse Transformationsmethode. Das
Verfahren wurde bereits ausgiebig diskutiert. Wir können daher den
Algorithmus sofort anschreiben: Erzeuge
verwendet man fast immer die inverse Transformationsmethode. Das
Verfahren wurde bereits ausgiebig diskutiert. Wir können daher den
Algorithmus sofort anschreiben: Erzeuge ![]() und setze
und setze
![]() - Prozessoren dagegen, wie zum
Beispiel der legendäre INTEL 8080, waren nur für logische Operationen
und einfache arithmetische Algebra ausgelegt. Hier waren andere Verfahren
durchaus von Wert.
- Prozessoren dagegen, wie zum
Beispiel der legendäre INTEL 8080, waren nur für logische Operationen
und einfache arithmetische Algebra ausgelegt. Hier waren andere Verfahren
durchaus von Wert.
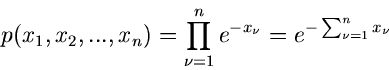
![]() gleichverteilte Zufallszahlen
gleichverteilte Zufallszahlen
![]() und bilden
und bilden
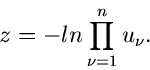
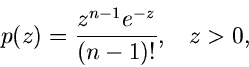
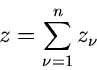
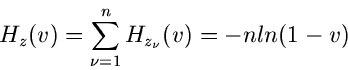
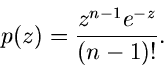
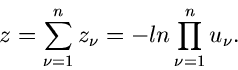
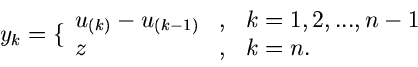
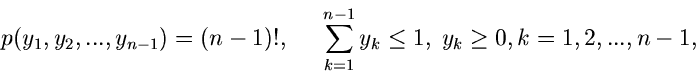
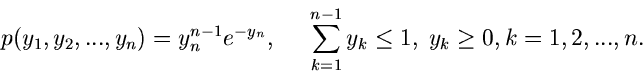
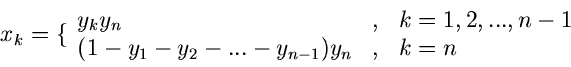
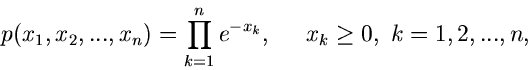
![]() und bilde
und bilde
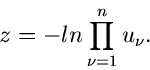
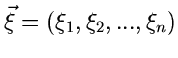 ist dann ein Vektor der
unabhängigen
ist dann ein Vektor der
unabhängigen ![]() Logarithmus- Berechnungen bei der inversen
Transformationsmethode. Demgegenüber stehen doppelt so viele Aufrufe des
Zufallszahlen- Generators und eine zusätzliche Sortierung von
Logarithmus- Berechnungen bei der inversen
Transformationsmethode. Demgegenüber stehen doppelt so viele Aufrufe des
Zufallszahlen- Generators und eine zusätzliche Sortierung von ![]() Zahlen. Der letztere Algorithmus erweist sich daher nur für Werte von
Zahlen. Der letztere Algorithmus erweist sich daher nur für Werte von
![]() zwischen etwa 3 und 6 der inversen Transformationsmethode überlegen.
Programmroutinen sind in JExponentialN1 und JExponentialN2 gelistet.
zwischen etwa 3 und 6 der inversen Transformationsmethode überlegen.
Programmroutinen sind in JExponentialN1 und JExponentialN2 gelistet.
![]() ,
,
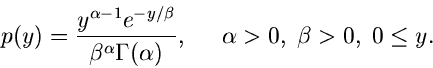
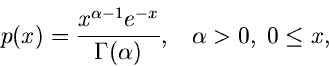
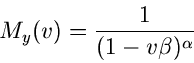
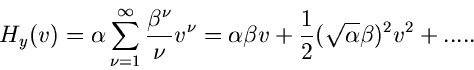
![]() und
und ![]() zwei Veränderliche aus Gammaverteilungen mit
Parametern
zwei Veränderliche aus Gammaverteilungen mit
Parametern ![]() und
und ![]() , d.h.
, d.h.
![]() und
und
![]() . Dann ist
. Dann ist ![]() eine
Veränderliche aus der Gammaverteilung
eine
Veränderliche aus der Gammaverteilung
![]() .
Der Beweis ist einfach und erfolgt über die logarithmisch erzeugende
Funktion.
.
Der Beweis ist einfach und erfolgt über die logarithmisch erzeugende
Funktion.
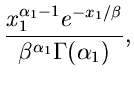
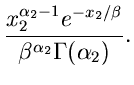
![]() Veränderliche
Veränderliche
![]() aus den
Gammaverteilungen
aus den
Gammaverteilungen
![]() ,
,
![]() , ....,
, ....,
![]() ist trivial und ergibt, daß die Veränderliche
ist trivial und ergibt, daß die Veränderliche
![]() aus
aus
![]() ist.
ist.
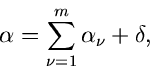
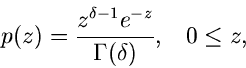
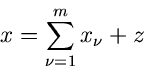
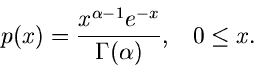
![]() ein.
Diese ist allgemein definiert durch
ein.
Diese ist allgemein definiert durch
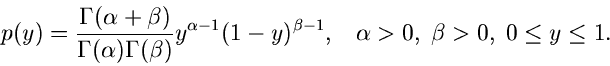
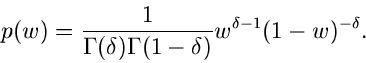
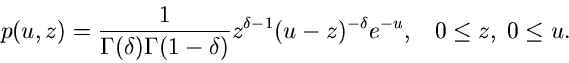
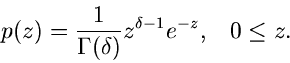
![]() mit
mit
![]() . Erzeuge
. Erzeuge
![]() und bilde
und bilde
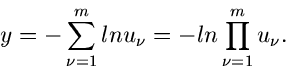
![]() .
Für große Werte von
.
Für große Werte von ![]() bzw
bzw ![]() kann die Erlang- Verteilung
kann die Erlang- Verteilung ![]() durch eine Normalverteilung ersetzt werden. Dieses folgt aus der Tatsache,
daß eine Veränderliche der Erlang- Verteilung als Summe von
durch eine Normalverteilung ersetzt werden. Dieses folgt aus der Tatsache,
daß eine Veränderliche der Erlang- Verteilung als Summe von ![]() Veränderlichen der Exponentialverteilung
Veränderlichen der Exponentialverteilung ![]() geschrieben werden kann.
Erwartungswert und Varianz der Erlang- Verteilung sind
für große Werte von
geschrieben werden kann.
Erwartungswert und Varianz der Erlang- Verteilung sind
für große Werte von ![]() durch
durch
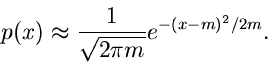
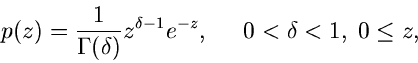
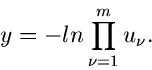
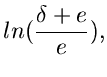
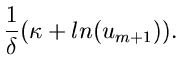
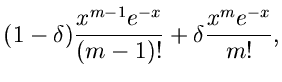
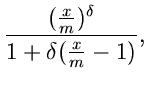
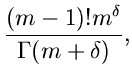
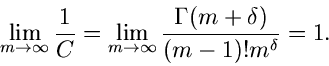
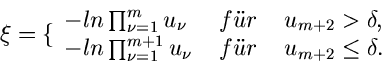
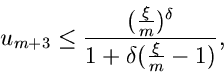
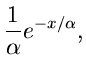
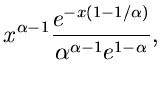
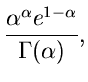
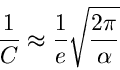
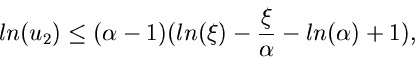
![]() in der Form
in der Form
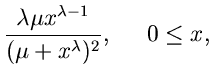
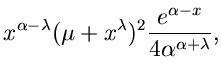
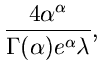
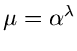 und
und
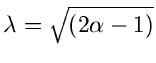 .
Die Erfolgswahrscheinlichkeit ist mit
.
Die Erfolgswahrscheinlichkeit ist mit

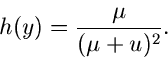
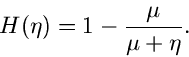
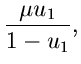
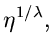
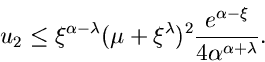
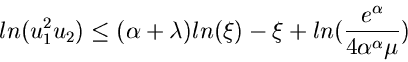
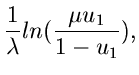
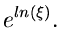
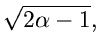
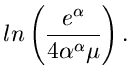
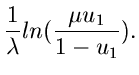
![]() ,
,
![\begin{displaymath}
h_{C}(x) = \frac{1}{\pi \lambda [ 1 +(\frac{x-\gamma}{\lambda})^{2}]}, \; \; \;
\; \; -\infty < x < \infty.
\end{displaymath}](img332.gif)
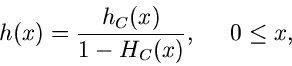
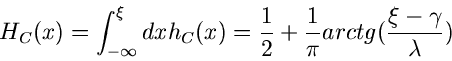
![\begin{displaymath}
\xi = \gamma + \lambda \; tg\{\pi [u_{1} (1-H_{C}(0)) + H_{C}(0)
-\frac{1}{2}] \}
\end{displaymath}](img335.gif)
![$\displaystyle [1 + (\frac{x-\gamma}{\lambda})^{2}] (\frac{x}{\gamma})^{\gamma}
e^{-x + \gamma},$](img337.gif)
![$\displaystyle \pi \lambda \gamma^{\gamma} \frac{[1-H_{C}(0)]}{\Gamma(\alpha)
e^{\gamma}},$](img338.gif)
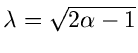 .
Der Algorithmus lautet: 1. Berechne in einem externen Programm
.
Der Algorithmus lautet: 1. Berechne in einem externen Programm
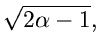
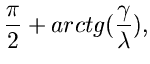
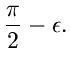
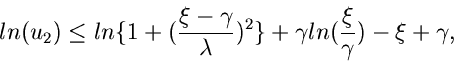
![]() mit
mit
![]() ist das folgende:
ist das folgende:
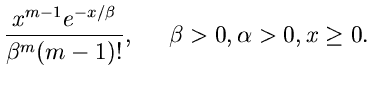
![$\displaystyle \frac{x^{\delta} e^{-x(1-1/\beta)}}{[\delta \beta/(\beta-1)]^{\delta}
e^{-\delta}}, \; \; \; \; \; \beta \not= 1,$](img350.gif)