Allgemeine Verfahren
Der n-dimensionale Gleichverteilungs- Generator.
In diesem Abschnitt werden wir eine systematische Darlegung der Verfahren
zur Simulation von zufälligen Veränderlichen bringen. In den Kapiteln
1 und 3 haben wir schon des öfteren Simulationsmethoden von zufälligen
Veränderlichen diskutiert, die alle auf dem folgenden Prinzip beruhten:
die Definition einer zufälligen Veränderlichen wurde Wort für Wort in
ein Rechnerprogramm übersetzt, wobei wir den experimentellen Versuch durch
den Aufruf eines Generators für Pseudozufallszahlen ersetzt hatten. Wir
erinnern in diesem Zusammenhang an die Simulation der Bernoulli- Verteilung
sowie der Multinominalverteilung in Kap.1.7. Auch die Simulation der 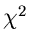 - Verteilung in
Kap.3.2 kann in diesem Zusammenhang erwähnt werden. In allen diesen
Beispielen mußten wir für die Erzeugung einer Zufallszahl der gesuchten
Verteilung im allgemeinen viele Aufrufe des Pseudozufallszahlen Generators
durchführen.
Eine Verbesserung der Generatoren liegt daher auf der Hand, nämlich die
Erzeugung von
- Verteilung in
Kap.3.2 kann in diesem Zusammenhang erwähnt werden. In allen diesen
Beispielen mußten wir für die Erzeugung einer Zufallszahl der gesuchten
Verteilung im allgemeinen viele Aufrufe des Pseudozufallszahlen Generators
durchführen.
Eine Verbesserung der Generatoren liegt daher auf der Hand, nämlich die
Erzeugung von  Zahlen in einem Aufruf. Als Beispiel benutzen wir
eine verbesserte Version des RANMAR- Generators, den wir im folgenden mit
RANMARN bezeichnen werden. Die Initialisierungsroutine heißt entsprechend
RMARINN.
Zahlen in einem Aufruf. Als Beispiel benutzen wir
eine verbesserte Version des RANMAR- Generators, den wir im folgenden mit
RANMARN bezeichnen werden. Die Initialisierungsroutine heißt entsprechend
RMARINN.
Die Methode der inversen Verteilungsfunktion
Sei  irgendeine Dichtefunktion einer kontinuierlichen Veränderlichen
irgendeine Dichtefunktion einer kontinuierlichen Veränderlichen
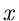 . Die integrale Verteilungsfunktion
. Die integrale Verteilungsfunktion
 |
(1) |
ist eine in dem Wertebereich
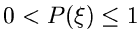 definierte Funktion. Wir
erzeugen eine gleichverteilte Zufallszahl
definierte Funktion. Wir
erzeugen eine gleichverteilte Zufallszahl ![$u \in [0,1]$](img7.gif) und setzen
und setzen
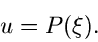 |
(2) |
Dann ergibt die Umkehrung,
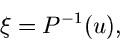 |
(3) |
eine gemäß der Dichtefunktion  verteilte Veränderliche
verteilte Veränderliche  .
.
Die direkte Anwendung der inversen Verteilungsfunktion ist zwar
außerordentlich beschränkt, da nur für wenige integrale
Verteilungsfunktionen die Umkehrung analytisch darstellbar ist. Trotzdem
bildet, wie wir im einzelnen noch sehen werden, die Methode der inversen
Verteilungsfunktion die Grundlage fast aller Simulationsmethoden von
zufälligen Veränderlichen.
Beispiel.
Ein einfaches Beispiel ist die Exponentialfunktion
Die integrale Verteilungsfunktion ist
Die Gleichung
läßt sich leicht nach  auflösen und ergibt
auflösen und ergibt
Im letzten Schritt haben wir die Tatsache benutzt, daß, wenn  eine im
Intervall
eine im
Intervall ![$[0,1]$](img16.gif) gleichverteilte Zufallszahl ist, so ist auch
gleichverteilte Zufallszahl ist, so ist auch  gleichverteilt in
gleichverteilt in ![$[0,1]$](img16.gif) .
.
Beispiel.
Ein zweites einfaches Beispiel ist die Dichtefunktion
Wegen
und
ist
ein Algorithmus zur Simulation der Verteilung  .
.
Methode der Tabellen- Darstellung
Eine Methode, die für kontinuierliche wie für diskrete Veränderliche
gleichermaßen anwendbar ist, ist die Tabellen- Darstellung der integralen
Verteilungsfunktion. Wir teilen die reelle Achse in 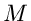 Teilintervalle
mit den Stützstellen
Teilintervalle
mit den Stützstellen
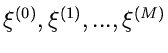 ein
und berechnen die Wahrscheinlichkeiten
ein
und berechnen die Wahrscheinlichkeiten
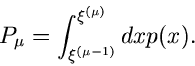 |
(4) |
Die integrale Verteilungsfunktion an der Stelle 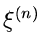 ist dann
ist dann
 |
(5) |
Wie bisher muß die Gleichung
nach  aufgelöst werden. Zu diesem Zweck erzeugen wir eine Zufallszahl
aufgelöst werden. Zu diesem Zweck erzeugen wir eine Zufallszahl
![$u_{1} \in [0,1]$](img27.gif) und bestimmen zunächst den Wert
und bestimmen zunächst den Wert 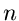 so, daß
so, daß
 |
(6) |
Anschließend erzeugen wir eine zweite Zufallszahl ![$u_{2}\in[0,1]$](img30.gif) und
interpolieren gemäß
und
interpolieren gemäß
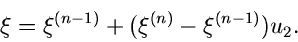 |
(7) |
 ist dann eine Veränderliche der Dichtefunktion
ist dann eine Veränderliche der Dichtefunktion  .
Diese Methode kann offensichtlich auch für jede diskrete Veränderliche
benutzt werden. Die integrale Verteilungsfunktion ist
.
Diese Methode kann offensichtlich auch für jede diskrete Veränderliche
benutzt werden. Die integrale Verteilungsfunktion ist
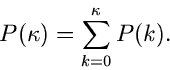 |
(8) |
Mit Hilfe einer gleichverteilten Zufallszahl ![$u \in [0,1]$](img7.gif) bestimmen wir
bestimmen wir
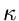 gemäß
gemäß
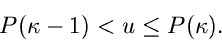 |
(9) |
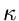 ist dann eine Veränderliche aus der Wahrscheinlichkeitsverteilung
ist dann eine Veränderliche aus der Wahrscheinlichkeitsverteilung
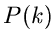 .
.
Man beachte, daß wir mit dem gleichen Funktionssymbol  die
Wahrscheinlichkeitsverteilung und die integrale Verteilung
dargestellt haben. Die Unterscheidung treffen wir mit Hilfe des Arguments.
die
Wahrscheinlichkeitsverteilung und die integrale Verteilung
dargestellt haben. Die Unterscheidung treffen wir mit Hilfe des Arguments.
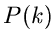 ist die Wahrscheinlichkeitsverteilung und
ist die Wahrscheinlichkeitsverteilung und 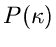 die integrale
Verteilung. Diese Schreibweise werden wir auch im folgenden beibehalten.
Eine sehr viel detailliertere Behandlung der Tabellen- Methode werden wir
noch als Vorbemerkung zur Simulation von diskreten Veränderlichen bringen.
die integrale
Verteilung. Diese Schreibweise werden wir auch im folgenden beibehalten.
Eine sehr viel detailliertere Behandlung der Tabellen- Methode werden wir
noch als Vorbemerkung zur Simulation von diskreten Veränderlichen bringen.
Mehrdimensionale Veränderliche
Ist eine Dichtefunktion mehrerer Veränderlicher vorgegeben, so lassen sich
zwei Fälle unterscheiden. Falls alle Veränderlichen unabhängig
voneinander sind,
 |
(10) |
so ergibt sich keine neue Situation. Die integrale Verteilungsfunktion ist
einfach
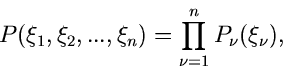 |
(11) |
und die Lösung ist
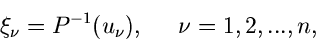 |
(12) |
wobei die
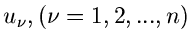 gleichverteilte Zufallszahlen
aus
gleichverteilte Zufallszahlen
aus ![$[0,1]$](img16.gif) sind.
sind.
Sofern andererseits die Veränderlichen 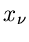 abhängig voneinander sind,
kann man auf zwei verschiedenen Wegen vorgehen. Einmal kann versucht werden,
mit Hilfe einer umkehrbar eindeutigen Transformation
abhängig voneinander sind,
kann man auf zwei verschiedenen Wegen vorgehen. Einmal kann versucht werden,
mit Hilfe einer umkehrbar eindeutigen Transformation
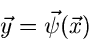 |
(13) |
eine Dichtefunktion 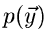 unabhängiger Veränderlicher
unabhängiger Veränderlicher 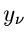
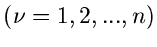 zu erhalten. Die Simulation des Vektors
zu erhalten. Die Simulation des Vektors 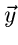 wird
dann wie oben geschildert durchgeführt. Die Rücktransformation
wird
dann wie oben geschildert durchgeführt. Die Rücktransformation
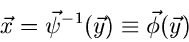 |
(14) |
ergibt dann den zufälligen Vektor 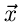 .
.
Oder aber, und das ist meist der bequemere Weg, man drückt die Dichtefunktion
durch bedingte Randverteilungen aus,
 |
(15) |
mit
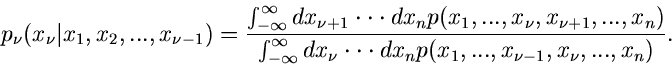 |
(16) |
Offensichtlich führt dann der folgende Algorithmus zum Ziel: Man bilde die integralen Verteilungsfunktionen,
erzeuge einen Vektor
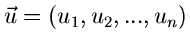 von
gleichverteilten Zufallszahlen aus
von
gleichverteilten Zufallszahlen aus ![$[0,1]$](img16.gif) und löse der Reihe nach die
Gleichungen
und löse der Reihe nach die
Gleichungen
Dieses ist offensichtlich kein Gleichungssystem, sondern eine Rekursion.
Für eine möglichst einfache Lösung dieser Rekursion ist häufig die
Reihenfolge der Veränderlichen wichtig. Für zwei Veränderliche z.B.
sind die beiden folgenden Darstellungen equivalent:
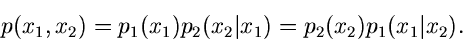 |
(19) |
Beispiel.
Als Beispiel zur vorherigen Bemerkung betrachten wir die Dichtefunktion
In der Darstellung
erhalten wir
und
Die Rekursion
beinhaltet die Lösung einer kubischen Gleichung, die zwar möglich ist,
aber dem Rechner viel Arithmetik abverlangt.
In der zweiten Darstellung
erhalten wir dagegen
und
Die daraus folgende Rekursion
ist wesentlich einfacher zu lösen als die kubische Gleichung bei der ersten
Darstellung, nämlich durch
Beispiel.
Das Paradebeispiel für die Transformation auf unabhängige Veränderliche
ist die Simulation der 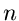 - dimensionalen allgemeinen Normalverteilung:
- dimensionalen allgemeinen Normalverteilung:
Wir schreiben die Kovarianzmatrix 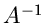 in der Form
in der Form
mit
Aus der numerischen Mathematik entnehmen wir die Behauptung, daß diese
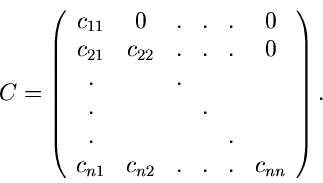
Matrix als Produkt zweier Dreiecksmatrizen ausgedrückt werden kann,
mit
Die Matrix 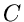 erhält man am einfachsten aus der Rekursionsrelation
erhält man am einfachsten aus der Rekursionsrelation
Transformiert man nun die Veränderliche 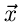 gemäß
gemäß
auf die Veränderliche 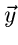 , so erhält man die unabhängige
Normalverteilung
, so erhält man die unabhängige
Normalverteilung
mit Mittelwerten 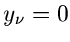 und Kovarianzmatrix
und Kovarianzmatrix
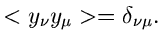 Die Rücktransformation ist denkbar einfach, und zwar
Die Rücktransformation ist denkbar einfach, und zwar
Die eigentliche Rechenarbeit besteht offensichtlich in der Berechnung der
Matrix 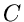 .
.
Wir wollen dieses Verfahren noch einmal für den Fall einer zweidimensionalen
Dichtefunktion mit
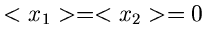 explizit aufschreiben. Die
Kovarianzmatrix lautet
explizit aufschreiben. Die
Kovarianzmatrix lautet
wobei wir die Varianzen bzw Kovarianzen
eingeführt haben. 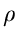 ist der hinreichend bekannte Korrelationskoeffizient.
Für die Elemente der Matriz
ist der hinreichend bekannte Korrelationskoeffizient.
Für die Elemente der Matriz 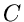 erhalten wir der Reihe nach
erhalten wir der Reihe nach
oder, übersichtlicher als Matriz geschrieben,
Die Dichtefunktion für 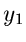 und
und 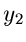 ist
ist
und die Rücktransformation nach 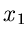 und
und 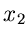 lautet
lautet
Dieses Ergebnis stimmt bis auf die Reihenfolge der Veränderlichen mit den
Ergebnissen in Kap.1.5 überein. Wegen der Symmetrie in den Veränderlichen
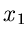 und
und 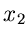 kommt es auf die Reihenfolge nicht an.
kommt es auf die Reihenfolge nicht an.
Reduktionsmethoden
Besonders wichtig für die Simulation eindimensionaler Veränderlicher
sind die Reduktionsmethoden. Hierbei geht man von einer mehrdimensionalen
Dichtefunktion aus, für die man bereits eine Simulationsverfahren
besitzten möge. Beispiele hierfür sind die 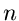 - dimensionale Verteilung
gleichverteilter unabhängiger Zufallszahlen aus
- dimensionale Verteilung
gleichverteilter unabhängiger Zufallszahlen aus ![$[0,1]$](img16.gif) oder die
oder die
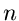 - dimensionale Normalverteilung. Man sucht dann geeignete Transformationen,
- dimensionale Normalverteilung. Man sucht dann geeignete Transformationen,
 |
(20) |
wobei die Randverteilung einer bestimmten Komponente 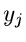 dann genau
der Verteilung der gesuchten Dichtefunktion entsprechen möge. Die Integration
zur Bildung von Randverteilungen ist in der Simulation trivial. Man braucht
alle übrigen Veränderlichen außer
dann genau
der Verteilung der gesuchten Dichtefunktion entsprechen möge. Die Integration
zur Bildung von Randverteilungen ist in der Simulation trivial. Man braucht
alle übrigen Veränderlichen außer 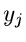 einfach nur zu ignorieren.
einfach nur zu ignorieren.
Wir beginnen mit dem einfachsten Fall, der Reduktion einer zweidimensionalen
Veränderlichen auf eine eindimensionale Veränderliche. Sei also
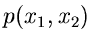 eine Dichtefunktion, für die wir bereits ein Verfahren
zur Simulation der Veränderlichen
eine Dichtefunktion, für die wir bereits ein Verfahren
zur Simulation der Veränderlichen 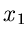 und
und 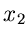 besitzen mögen.
Wir transformieren gemäß
besitzen mögen.
Wir transformieren gemäß
und erhalten eine Dichtefunktion
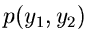 für die Veränderlichen
für die Veränderlichen
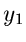 und
und 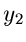 . Die Randverteilungen
. Die Randverteilungen
sind nun häufig gesuchte Dichtefunktionen, deren Simulation damit auf die
Simulation der Dichtefunktion
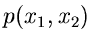 zurückgeführt ist.
zurückgeführt ist.
Beispiel.
Als Beispiel diskutieren wir die zweidimensionale unabhängige
Normalverteilung mit Mittelwerten
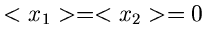 und Varianzen
und Varianzen
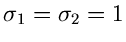 ,
,
Die Transformation
führt auf die Dichtefunktion:
und die Integration über 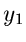 liefert
liefert
Diese Dichtefunktion nennt man die Cauchy- Verteilung. Man erhält also
eine Veränderliche der Cauchy- Verteilung, indem man die Veränderlichen
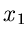 und
und 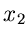 aus einer zweidimensionalen unabhängigen Normalverteilung
mit
aus einer zweidimensionalen unabhängigen Normalverteilung
mit
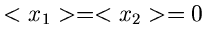 und Varianzen
und Varianzen
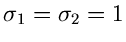 durcheinander dividiert:
durcheinander dividiert:
Beispiele.
Weitere Beispiele sind die Verteilungsfunktionen, die man aus der Reduktion
von 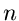 unabhängigen gleichverteilten Zufallszahlen erhält. Seien also
unabhängigen gleichverteilten Zufallszahlen erhält. Seien also
![$u_{\nu} \in [0,1], \; \nu=1,2,...,n$](img148.gif) , und setzen wir
, und setzen wir
so erhält man die Randverteilungen
Die erste Verteilung haben wir in vorherigen Abschnitten schon mehrmals
diskutiert, die zweite Verteilung haben wir bei der Behandlung geordneter Statistiken abgeleitet.
Für 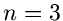 ist insbesondere die Zufallszahl
ist insbesondere die Zufallszahl
durch die einfache Dichtefunktion
darstellbar (siehe Kap.3.1).
Beispiel.
Ein anderes wichtiges Beispiel hatten wir bereits bei der Herleitung
der 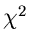 - Verteilung gefunden. Wenn
- Verteilung gefunden. Wenn
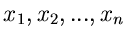 unabhängig normalverteilt sind, mit Mittelwerten
unabhängig normalverteilt sind, mit Mittelwerten
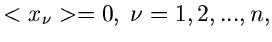 und Varianzen
und Varianzen
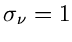 ,
,
dann ist die Summe der Quadrate
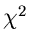 - verteilt mit der Dichtefunktion
- verteilt mit der Dichtefunktion
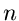 nennt man die Anzahl der Freiheitsgrade.
nennt man die Anzahl der Freiheitsgrade.
Composition- Methode
Wir kommen noch einmal zurück auf die Formel
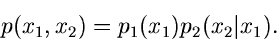 |
(26) |
Diese Formel gestattet in vielen Fällen eine bequeme Simulation der
Randverteilung
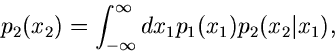 |
(27) |
sofern Algorithmen zur Simulation von 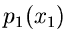 und
und
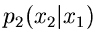 bereits existieren. Dieses Verfahren ist in der Literatur
auch unter dem englischen Ausdruck Composition- Methode bekannt.
bereits existieren. Dieses Verfahren ist in der Literatur
auch unter dem englischen Ausdruck Composition- Methode bekannt.
Die Composition Methode kann in einfacher Weise auf gemischte
Verteilungen erweitert werden, wobei dann allerdings
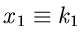 eine diskrete Veränderliche wird. Wir schreiben
eine diskrete Veränderliche wird. Wir schreiben
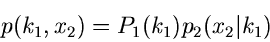 |
(28) |
und
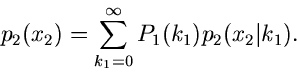 |
(29) |
Der Algorithmus lautet also: Bilde die integralen Verteilungen
bzw
und löse die Bestimmungsgleichungen
bzw
wobei wie immer
![$u_{1}, u_{2} \in [0,1]$](img178.gif) zwei gleichverteilte Zufallszahlen
sind.
zwei gleichverteilte Zufallszahlen
sind. 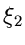 ist dann eine Veränderliche der Dichtefunktion
ist dann eine Veränderliche der Dichtefunktion 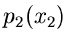 .
.
Beispiel.
Das wichtigste Beispiel in diesem Rahmen ist eine Simulation der
Normalverteilung. Wir beginnen mit der zweidimensionalen Normalverteilung
und transformieren gemäß
mit
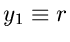 und
und
 . Dieses führt auf die
Dichtefunktion der Veränderlichen
. Dieses führt auf die
Dichtefunktion der Veränderlichen 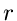 und
und 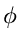 :
:
Wir faktorisieren die Dichtefunktion in der Form
und identifizieren
Für 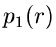 und
und
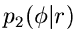 haben wir aber bereits Algorithmen
zur Simulation.
haben wir aber bereits Algorithmen
zur Simulation. 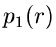 kann mit der inversen Transformationsmethode
(siehe Beispiel am Anfang dieses Kapitels) gelöst werden und
kann mit der inversen Transformationsmethode
(siehe Beispiel am Anfang dieses Kapitels) gelöst werden und
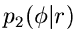 ist eine
Gleichverteilung in
ist eine
Gleichverteilung in ![$[0,2\pi ]$](img195.gif) . Damit erhalten wir den Algorithmus
. Damit erhalten wir den Algorithmus
mit
![$u_{1}, u_{2} \in [0,1]$](img178.gif) . Die Rücktransformation gemäß (43)
liefert zwei normalverteilte unabhängige Veränderliche.
. Die Rücktransformation gemäß (43)
liefert zwei normalverteilte unabhängige Veränderliche.
Beispiel.
Gesucht sei eine Simulation der Dichtefunktion
Wir gehen von der zweidimensionalen Dichtefunktion
aus und berechnen
Damit ergibt sich für die integralen Verteilungsfunktionen
Mit Hilfe von zwei gleichverteilten Zufallszahlen
![$u_{1}, u_{2} \in [0,1]$](img178.gif) erhalten wir die Lösung
erhalten wir die Lösung
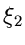 ist dann die gesuchte Veränderliche der Dichtefunktion
ist dann die gesuchte Veränderliche der Dichtefunktion
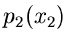 .
.
Beispiel.
Die Composition Methode kann besonders vorteilhaft für die
Simulation von Dichtefunktionen verwendet werden, die als Reihenentwicklung
darstellbar sind,
Die Normierung verlangt, daß
Wir setzen
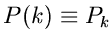 und
und
Damit erhalten wir der Reihe nach
und
Wir erzeugen zwei Zufallszahlen
![$u_{1}, u_{2} \in [0,1]$](img178.gif) und erhalten
und erhalten
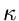 aus der Ungleichung
aus der Ungleichung
sowie  aus der Gleichung
aus der Gleichung
 ist dann eine Veränderliche der Dichtefunktion
ist dann eine Veränderliche der Dichtefunktion  .
.
Das Verfahren kann verallgemeinert werden für Summen beliebiger
Dichtefunktionen 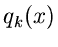 ,
,
mit
Die zugrundeliegende zweidimensionale Dichtefunktion ist also
mit
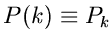 . Die Randverteilungen sind also
. Die Randverteilungen sind also
Mit Hilfe der integralen Verteilungsfunktionen
lautet die Formulierung des Verfahrens: Erzeuge zwei Zufallszahlen
![$u_{1}, u_{2} \in [0,1]$](img178.gif) und bestimme
und bestimme 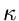 aus
aus
Löse die Gleichung
nach  auf.
auf.  ist dann eine Veränderliche der Dichtefunktion
ist dann eine Veränderliche der Dichtefunktion
 .
.
Verwerfungsmethoden
Bei der Verwerfungsmethode stellen wir die gesuchte Dichtefunktion 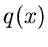 in der Form
in der Form
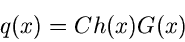 |
(36) |
dar. Dazu schlagen wir folgenden Weg ein. Wir beginnen mit einer
zweidimensionalen Dichtefunktion in der üblichen Darstellung
Das Integral über 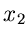 in den Grenzen von
in den Grenzen von 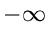 bis
bis 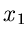 kann
geschrieben werden als
kann
geschrieben werden als
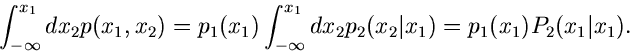 |
(37) |
Die rechts stehende Wahrscheinlichkeit  lautet ausführlich
geschrieben:
lautet ausführlich
geschrieben:
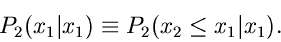 |
(38) |
Die linke Seite von (37) ist nun eine Dichtefunktion der Veränderlichen
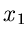 , die aber im allgemeinen nicht auf 1 normiert ist. Wir setzen daher
, die aber im allgemeinen nicht auf 1 normiert ist. Wir setzen daher
und erhalten
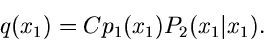 |
(39) |
Ein Vergleich mit (36) zeigt, daß
Aus dieser Identifikation ergibt sich, daß für 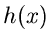 ,
, 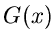 und
und 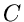 die folgenden Bedingungen erfüllt sein müssen:
die folgenden Bedingungen erfüllt sein müssen:
Wir hatten die integrale bedingte Verteilungsfunktion
 definiert als Wahrscheinlichkeit dafür, daß die
Veränderliche
definiert als Wahrscheinlichkeit dafür, daß die
Veränderliche
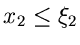 , aber unter der Vorraussetzung, daß
die Veränderliche
, aber unter der Vorraussetzung, daß
die Veränderliche 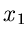 einen festen Wert
einen festen Wert 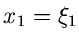 annimmt.
Die Funktion
annimmt.
Die Funktion
 gibt dann die
Wahrscheinlichkeit an, daß die Veränderliche
gibt dann die
Wahrscheinlichkeit an, daß die Veränderliche 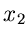 kleiner als der
Wert
kleiner als der
Wert
 sein soll, unter der Vorraussetzung, daß der
Wert für
sein soll, unter der Vorraussetzung, daß der
Wert für
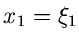 bereits festliegt.
Offensichtlich bedeutet dieses, daß
bereits festliegt.
Offensichtlich bedeutet dieses, daß 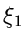 nur dann eine Veränderliche der
Dichtefunktion
nur dann eine Veränderliche der
Dichtefunktion
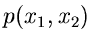 sein kann, wenn die Bedingung
sein kann, wenn die Bedingung
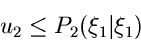 |
(43) |
mit einer zweiten Zufallszahl
![$u_{2}\in[0,1]$](img30.gif) erfüllt ist.
erfüllt ist.
Zusammengefaßt erhalten wir folgenden Algorithmus: Erzeuge zwei Zufallszahlen
![$u_{1}, u_{2} \in [0,1]$](img178.gif) , löse die Gleichung
, löse die Gleichung
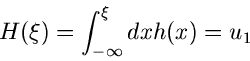 |
(44) |
nach  auf und prüfe, ob
auf und prüfe, ob
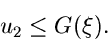 |
(45) |
Wenn diese Bedingung nicht erfüllt ist, verwerfen wir  und beginnen von vorne.
und beginnen von vorne.
Eine wichtige Größe bei dieser Methode ist die Zahl 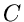 . Zunächst ist
klar, daß
. Zunächst ist
klar, daß 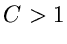 ist (siehe (42)). Wie man sich leicht klarmachen
kann, ist
ist (siehe (42)). Wie man sich leicht klarmachen
kann, ist 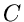 die mittlere Anzahl der Versuche, bis zu der die Ungleichung
(45) erfüllt ist. Die Größe
die mittlere Anzahl der Versuche, bis zu der die Ungleichung
(45) erfüllt ist. Die Größe 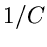 nennt man daher auch die Erfolgswahrscheinlichkeit oder Effizienz des Verfahrens.
Je größer die Effizienz, desto schneller ist das Verwerfungsverfahren.
nennt man daher auch die Erfolgswahrscheinlichkeit oder Effizienz des Verfahrens.
Je größer die Effizienz, desto schneller ist das Verwerfungsverfahren.
Der optimale Wert für 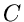 wäre eigentlich
wäre eigentlich 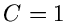 . Das ist natürlich nicht
möglich.
. Das ist natürlich nicht
möglich. 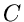 erreicht dagegen umso näher den Wert 1, je größer die
Funktion
erreicht dagegen umso näher den Wert 1, je größer die
Funktion 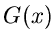 ist. Man muß also immer versuchen, die Funktion
ist. Man muß also immer versuchen, die Funktion 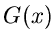 maximal zu wählen, aber unter Einhaltung der Nebenbedingung
maximal zu wählen, aber unter Einhaltung der Nebenbedingung
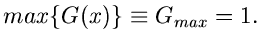
Beispiel.
Ein Beispiel, das auf die allgemeine Verwerfungsmethode zurückgeht, ist das
folgende. Gesucht ist ein Simulationsalgorithmus der Dichtefunktion
Wir setzen
Der Grund für die gewählte Aufteilung der Funktion 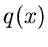 in die
Faktoren
in die
Faktoren 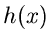 ,
, 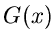 und
und 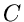 folgt aus unseren obigen Überlegungen.
Die Wahl der Funktion
folgt aus unseren obigen Überlegungen.
Die Wahl der Funktion 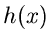 ergibt sich aus der Normierung
ergibt sich aus der Normierung
Für 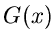 ist die Bedingung
ist die Bedingung
offensichtlich für 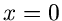 und
und 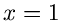 erfüllt. Der Ausdruck für
erfüllt. Der Ausdruck für 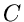 folgt
dann aus
folgt
dann aus
Die integralen Verteilungsfunktionen sind
Auf diesen Ergebnissen aufbauend, können wir folgenden Algorithmus
entwerfen: Erzeuge zwei Zufallszahlen
![$u_{1}, u_{2} \in [0,1]$](img178.gif) . Wenn
. Wenn
dann prüfe, ob
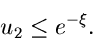 |
(46) |
Falls dagegen 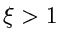 , dann ersetze
, dann ersetze  durch
durch
und prüfe, ob
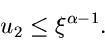 |
(47) |
Wenn die Bedingung (46) bzw (47) nicht erfüllt ist, beginne von vorne.
Dieses Beispiel finden Sie in dem folgenden
Applet unter der Bezeichnung Gamma.Unter dem weiteren Menupunkt BreitWigner finden Sie eine Simulation von BreitWigner- Verteilungen
mit einem speziellen Verfahren, das wir im folgenden diskutieren werden.
Das von Neumann'sche Verfahren.
Der Mathematiker von Neumann hat das Verwerfungsverfahren in der folgenden
Form vorgeschlagen.
Sei 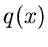 eine im Intervall
eine im Intervall
 definierte Dichtefunktion, für die wir einen Simulationsalgorithmus suchen.
Wir setzen für
definierte Dichtefunktion, für die wir einen Simulationsalgorithmus suchen.
Wir setzen für 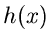 die spezielle Gleichverteilung
die spezielle Gleichverteilung
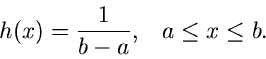 |
(48) |
Dann können wir 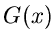 durch die vorgegebene
Dichtefunktion
durch die vorgegebene
Dichtefunktion 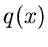 ausdrücken. Wegen
ausdrücken. Wegen
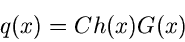 |
(49) |
erhalten wir
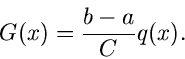 |
(50) |
Die Zahl 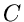 muß hierbei so gewählt werden, daß
muß hierbei so gewählt werden, daß
 für
für ![$x \in [a,b]$](img291.gif) , d.h.
, d.h.
oder
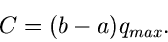 |
(51) |
Hierbei ist 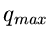 das Maximum der Dichtefunktion
das Maximum der Dichtefunktion 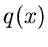 .
Wir können dann schreiben:
.
Wir können dann schreiben:
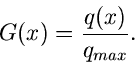 |
(52) |
Wir formulieren das Verfahren: Erzeuge zwei Zufallszahlen
![$u_{1}, u_{2} \in [0,1]$](img178.gif) und berechne
und berechne
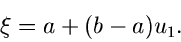 |
(53) |
Wenn dann
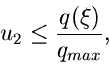 |
(54) |
ist  eine Veränderliche der Dichtefunktion
eine Veränderliche der Dichtefunktion 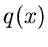 , sonst beginne
von vorne.
, sonst beginne
von vorne.
Das besondere an dem Verfahren von v. Neumann ist offensichtlich, daß keine
inverse Funktion berechnet werden muß. Der Algorithmus ist auch für die
kompliziertesten Dichtefunktionen 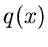 universell
anwendbar. Der Nachteil des Verfahrens ist, daß für große Intervalle
universell
anwendbar. Der Nachteil des Verfahrens ist, daß für große Intervalle
![$[a,b]$](img298.gif) die Erfolgswahrscheinlichkeit
die Erfolgswahrscheinlichkeit 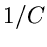 klein wird.
klein wird.
Beispiel.
Wir diskutieren das v. Neumannsche Verfahren an dem einfachen Beispiel
Das Maximum dieser Funktion wird offensichtlich für 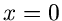 angenommen,
angenommen,
Mit 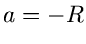 und
und 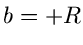 erhalten wir
erhalten wir
Das Verfahren lautet also: Erzeuge
![$u_{1}, u_{2} \in [0,1]$](img178.gif) , berechne
, berechne
und prüfe, ob
Wenn diese Bedingung erfüllt ist, ist  eine Veränderliche der
Dichtefunktion
eine Veränderliche der
Dichtefunktion 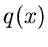 . Wenn nicht, verwerfe
. Wenn nicht, verwerfe  und beginne von vorne.
und beginne von vorne.
Beispiel
Die Verwerfungsmethode von Neumann wird im folgenden
Applet an einer pathologischen Dichtefunktionen
erläutert. Wir hatten oben in diesem Kapitel bereits eine Simulation der Cauchy- Verteilung
diskutiert. Diese Vertelung ist im Bereich von 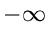 bis
bis 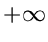 auf eins normiert,
auf eins normiert,
Das merkwürdige ist allerdings, daß man keine höheren Momente berechnen kann, d.h.
Man benötigt also einen Konvergenz erzeugenden Multiplikator. Die Chauchy- Verteilung kommt
hauptsächlichst in der Teilchenphysik zur Beschreibung von Resonanzen zum Einsatz. In diesem
Fall ist der Multiplikator bereits von der Physik her vorgegeben, und zwar der Phasenraum- Faktor,
der für die Energie- und Impulserhaltung sorgt.
Man nennt die Verteilung dann auch die Breit- Wigner- Verteilung. Mit der Transformation
erhält man
Der Phasenraumfaktor kann vereinfacht geschrieben werden als
und die Gesamtverteilung ist
In dem Applet studieren wir die Summe dreier Resonanzen. Sie werden bemerken, daß das Verwerfungsverfahren
kein besonders effektiver Algorithmus mit einer Effizienz von nur wenigen Prozenten ist und daher auch nur
im Notfall eingesetzt werden sollte.
In diesem und in allen folgenden Applets dieses Kapitels ist die Bedienung immer gleich. Im Menu Generator wählen wir zunächst einen bestimmten Generator aus. Es erscheint ein weiteres kleines Fenster, in dem Sie
die Parameter der Verteilung ändern können. Auf jeden Fall müssen Sie dieses Fenster mit OK quittieren. Im Menu Plots können dann mehrere Fenster
geöffnet werden, wie z.B. die Visualisierung der erzeugten Verteilung und die exakte Kurve der mathematischen
Funktion der Verteilung. Bei Anklicken des Source- Buttons wird ein Fenster mit dem Source- Code
des Algorithmus aufgeklappt. Bei Start beginnen wir die Simulation, bei Stop wird sie
abgebrochen.
Die Methode von Forsythe
Eine etwas komplizierte Methode ist von Forsythe entwickelt worden.
Wir behandeln dieses Verfahren etwas ausführlicher, weil es insbeondere
gestattet, für bestimmte Lösungen des Sattelpunktverfahrens
(siehe Kap.3.4) Simulationsprogramme zu entwickeln. Die Methode ist
anwendbar für irgendeine Dichtefunktion in der Form
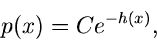 |
(55) |
wobei 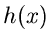 eine stetig anwachsende Funktion von
eine stetig anwachsende Funktion von 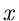 im Bereich
im Bereich ![$[0,\infty]$](img318.gif) ist. Wir unterteilen die positive reelle Achse in
ist. Wir unterteilen die positive reelle Achse in  Intervalle zwischen
den Stützstellen
Intervalle zwischen
den Stützstellen
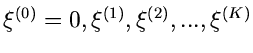 und
berechnen
und
berechnen
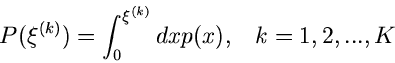 |
(56) |
und die Intervallängen
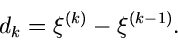 |
(57) |
Wählt man die Stützstellen  nun so, daß stets
nun so, daß stets
![\begin{displaymath}
g_{k}(x) = h(x) - h(\xi^{(k-1)}) \leq 1 \; \; \;
\forall \; x \in [\xi^{(k-1)},\xi^{(k)}],
\end{displaymath}](img324.gif) |
(58) |
so führt der folgende Algorithmus
auf ein Simulationsprogramm für die Dichtefunktion  : Erzeuge zwei Zufallszahlen
: Erzeuge zwei Zufallszahlen
![$u_{-1},u_{0} \in [0,1]$](img325.gif) . Bestimme
. Bestimme 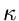 so, daß
so, daß
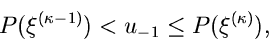 |
(59) |
und wähle einen Wert der Veränderlichen 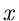 im
im 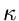 -ten Intervall gemäß
-ten Intervall gemäß
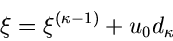 |
(60) |
Erzeuge solange weitere Zufallszahlen
![$u_{\nu} \in [0,1]$](img328.gif) ,
, 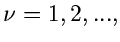 bis die Bedingung
bis die Bedingung
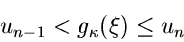 |
(61) |
erfüllt ist. Wenn 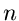 ungerade ist, akzeptiere
ungerade ist, akzeptiere  als Veränderliche der
Dichtefunktion
als Veränderliche der
Dichtefunktion  . Wenn dagegen
. Wenn dagegen 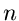 gerade ist, verwerfe
gerade ist, verwerfe  und beginne
von vorne.
und beginne
von vorne.
Die Forsythe- Methode erscheint auf den ersten Blick ziemlich umständlich
und zeitraubend. Der große Vorteil liegt jedoch darin, daß die
Exponentialfunktion nur in der Initialisierungsphase berechnet werden muß,
ähnlich wie in der Tabellen- Darstellung. Gegenüber der Tabellen- Methode
liefert die Forsythe- Methode jedoch eine exakte Simulation der zufälligen
Veränderlichen
Beispiel.
Als erstes Beispiel behandeln wir eine Simulation der normalisierten
Exponentialfunktion
d.h.
Bei der folgenden Wahl der Stützstellen,
gilt
und
Ersichtlich genügen etwa 10 Stützstellen
 .
Das Verfahren lautet also im einzelnen: 1. Berechne die Größen
.
Das Verfahren lautet also im einzelnen: 1. Berechne die Größen
in einem externen Initialisierungsprogram. 2. Erzeuge zwei Zufallszahlen
![$u_{-1},u_{0} \in [0,1]$](img325.gif) , bestimme
, bestimme 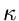 gemäß
gemäß
und  gemäß
gemäß
Erzeuge solange weitere Zufallszahlen
![$u_{1}, u_{2},...,u_{n} \in [0,1],$](img347.gif) bis die Bedingung
bis die Bedingung
erfüllt ist. Falls 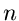 ungerade ist, akzeptiere
ungerade ist, akzeptiere  als zufällige
Veränderliche der Dichtefunktion
als zufällige
Veränderliche der Dichtefunktion  , sonst beginne von vorne bei
Punkt 2.
, sonst beginne von vorne bei
Punkt 2.
Beispiel.
Als zweites Beispiel behandeln wir die Dichtefunktion
d.h. die normalisierte rechte Hälfte der Standard- Normalverteilung.
Jetzt ist
und die folgende Wahl der Stützstellen,
erfüllt die Bedingungen der Forsythe- Methode. Wir erhalten
und
Die Tabellenwerte
müssen wiederum extern berechnet werden. Ersichtlich genügen in diesem
Beispiel ungefähr 5 Stützstellen, sodaß der Algorithmus folgendermaßen
formuliert werden kann:
1. Setze
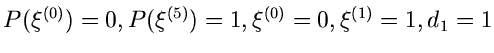 und berechne in einem externen
Programm
und berechne in einem externen
Programm
2. Erzeuge zwei Zufallszahlen
![$u_{-1},u_{0} \in [0,1]$](img325.gif) , bestimme
, bestimme
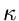 gemäß
gemäß
und  gemäß
gemäß
Erzeuge solange weitere Zufallszahlen
![$u_{\nu} \in [0,1], \nu = 1,2,3,...$](img368.gif) ,
bis die Bedingung
,
bis die Bedingung
erfüllt ist. Falls 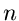 ungerade ist, akzeptiere
ungerade ist, akzeptiere  als Veränderliche
der Dichtefunktion
als Veränderliche
der Dichtefunktion  , sonst beginne von vorne bei Punkt 2.
, sonst beginne von vorne bei Punkt 2.
Harm Fesefeldt
2006-07-10
![]() irgendeine Dichtefunktion einer kontinuierlichen Veränderlichen
irgendeine Dichtefunktion einer kontinuierlichen Veränderlichen
![]() . Die integrale Verteilungsfunktion
. Die integrale Verteilungsfunktion


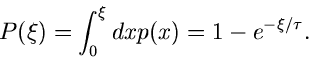
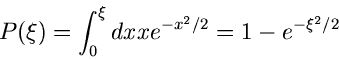
![]() Teilintervalle
mit den Stützstellen
Teilintervalle
mit den Stützstellen
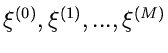 ein
und berechnen die Wahrscheinlichkeiten
ein
und berechnen die Wahrscheinlichkeiten
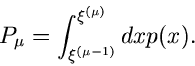

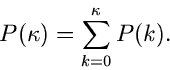
![]() die
Wahrscheinlichkeitsverteilung und die integrale Verteilung
dargestellt haben. Die Unterscheidung treffen wir mit Hilfe des Arguments.
die
Wahrscheinlichkeitsverteilung und die integrale Verteilung
dargestellt haben. Die Unterscheidung treffen wir mit Hilfe des Arguments.
![]() ist die Wahrscheinlichkeitsverteilung und
ist die Wahrscheinlichkeitsverteilung und ![]() die integrale
Verteilung. Diese Schreibweise werden wir auch im folgenden beibehalten.
Eine sehr viel detailliertere Behandlung der Tabellen- Methode werden wir
noch als Vorbemerkung zur Simulation von diskreten Veränderlichen bringen.
die integrale
Verteilung. Diese Schreibweise werden wir auch im folgenden beibehalten.
Eine sehr viel detailliertere Behandlung der Tabellen- Methode werden wir
noch als Vorbemerkung zur Simulation von diskreten Veränderlichen bringen.

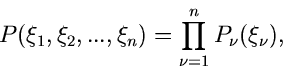
![]() abhängig voneinander sind,
kann man auf zwei verschiedenen Wegen vorgehen. Einmal kann versucht werden,
mit Hilfe einer umkehrbar eindeutigen Transformation
abhängig voneinander sind,
kann man auf zwei verschiedenen Wegen vorgehen. Einmal kann versucht werden,
mit Hilfe einer umkehrbar eindeutigen Transformation
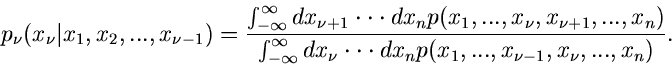
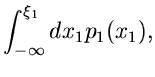
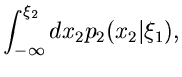
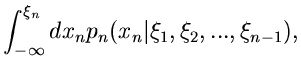
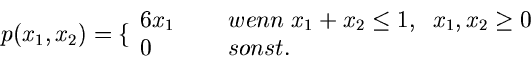
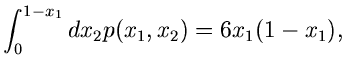
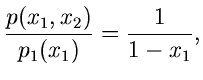
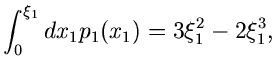
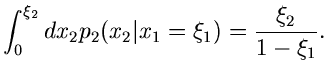

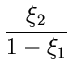

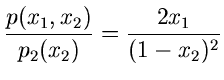
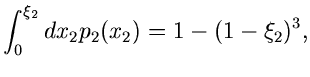
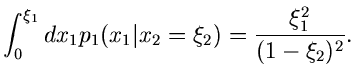
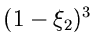
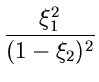
![]() - dimensionalen allgemeinen Normalverteilung:
- dimensionalen allgemeinen Normalverteilung:

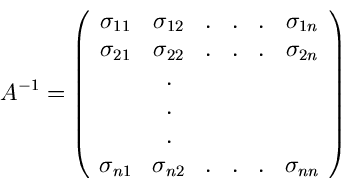
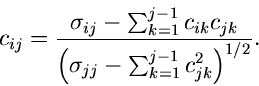
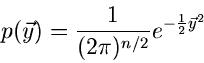
![]() explizit aufschreiben. Die
Kovarianzmatrix lautet
explizit aufschreiben. Die
Kovarianzmatrix lautet
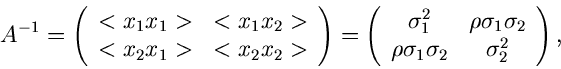

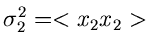
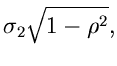
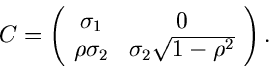
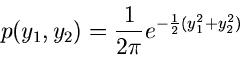
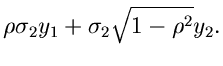
![]() - dimensionale Verteilung
gleichverteilter unabhängiger Zufallszahlen aus
- dimensionale Verteilung
gleichverteilter unabhängiger Zufallszahlen aus ![]() oder die
oder die
![]() - dimensionale Normalverteilung. Man sucht dann geeignete Transformationen,
- dimensionale Normalverteilung. Man sucht dann geeignete Transformationen,
![]() eine Dichtefunktion, für die wir bereits ein Verfahren
zur Simulation der Veränderlichen
eine Dichtefunktion, für die wir bereits ein Verfahren
zur Simulation der Veränderlichen ![]() und
und ![]() besitzen mögen.
Wir transformieren gemäß
besitzen mögen.
Wir transformieren gemäß

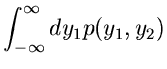
![]() und Varianzen
und Varianzen
![]() ,
,


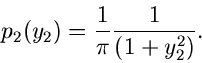

![]() unabhängigen gleichverteilten Zufallszahlen erhält. Seien also
unabhängigen gleichverteilten Zufallszahlen erhält. Seien also
![]() , und setzen wir
, und setzen wir

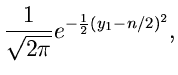
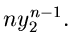
![]() ist insbesondere die Zufallszahl
ist insbesondere die Zufallszahl
![]() - Verteilung gefunden. Wenn
- Verteilung gefunden. Wenn
![]() unabhängig normalverteilt sind, mit Mittelwerten
unabhängig normalverteilt sind, mit Mittelwerten
![]() und Varianzen
und Varianzen
![]() ,
,
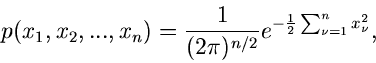
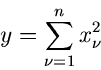
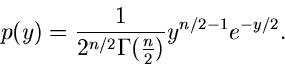
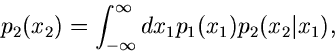
![]() eine diskrete Veränderliche wird. Wir schreiben
eine diskrete Veränderliche wird. Wir schreiben
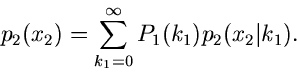
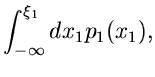
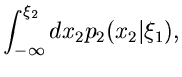
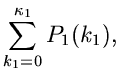
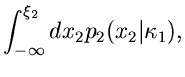

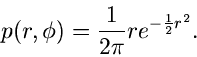
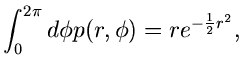
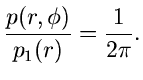

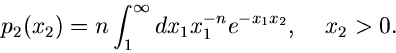
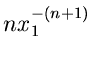

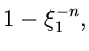
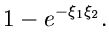

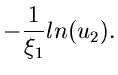
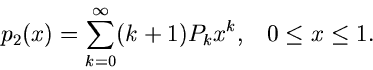

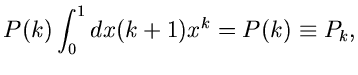

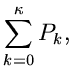
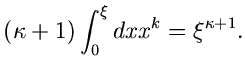
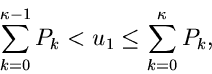
![]() ,
,
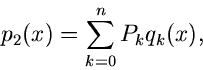
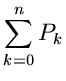

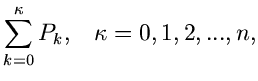
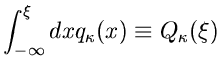
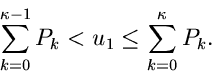
![]() in der Form
in der Form
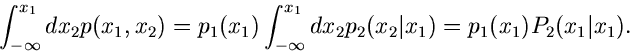
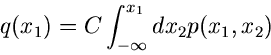
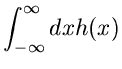
![]() , löse die Gleichung
, löse die Gleichung
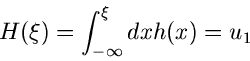
![]() . Zunächst ist
klar, daß
. Zunächst ist
klar, daß ![]() ist (siehe (42)). Wie man sich leicht klarmachen
kann, ist
ist (siehe (42)). Wie man sich leicht klarmachen
kann, ist ![]() die mittlere Anzahl der Versuche, bis zu der die Ungleichung
(45) erfüllt ist. Die Größe
die mittlere Anzahl der Versuche, bis zu der die Ungleichung
(45) erfüllt ist. Die Größe ![]() nennt man daher auch die Erfolgswahrscheinlichkeit oder Effizienz des Verfahrens.
Je größer die Effizienz, desto schneller ist das Verwerfungsverfahren.
nennt man daher auch die Erfolgswahrscheinlichkeit oder Effizienz des Verfahrens.
Je größer die Effizienz, desto schneller ist das Verwerfungsverfahren.
![]() wäre eigentlich
wäre eigentlich ![]() . Das ist natürlich nicht
möglich.
. Das ist natürlich nicht
möglich. ![]() erreicht dagegen umso näher den Wert 1, je größer die
Funktion
erreicht dagegen umso näher den Wert 1, je größer die
Funktion ![]() ist. Man muß also immer versuchen, die Funktion
ist. Man muß also immer versuchen, die Funktion ![]() maximal zu wählen, aber unter Einhaltung der Nebenbedingung
maximal zu wählen, aber unter Einhaltung der Nebenbedingung
![]()
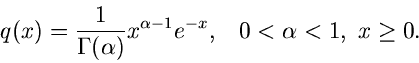
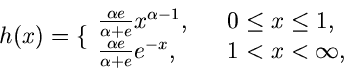
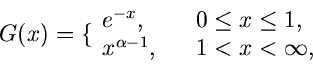
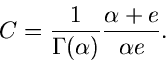
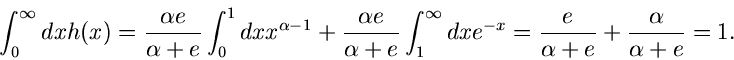

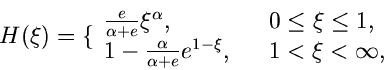
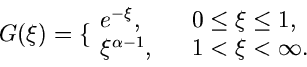
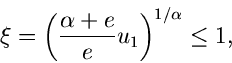
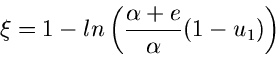
![]() eine im Intervall
eine im Intervall
![]() definierte Dichtefunktion, für die wir einen Simulationsalgorithmus suchen.
Wir setzen für
definierte Dichtefunktion, für die wir einen Simulationsalgorithmus suchen.
Wir setzen für ![]() die spezielle Gleichverteilung
die spezielle Gleichverteilung
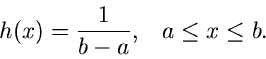
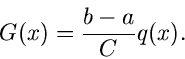
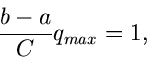
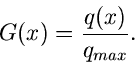
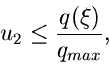
![]() universell
anwendbar. Der Nachteil des Verfahrens ist, daß für große Intervalle
universell
anwendbar. Der Nachteil des Verfahrens ist, daß für große Intervalle
![]() die Erfolgswahrscheinlichkeit
die Erfolgswahrscheinlichkeit ![]() klein wird.
klein wird.
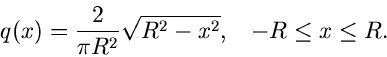
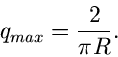
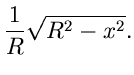
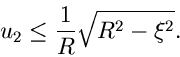
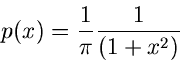
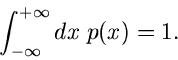
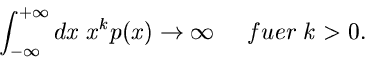
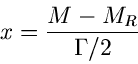
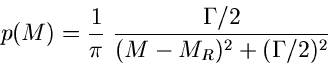
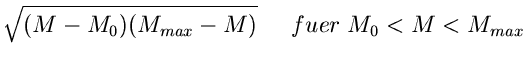
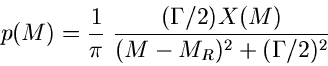
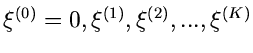 und
berechnen
und
berechnen
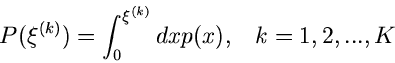
 .
Das Verfahren lautet also im einzelnen: 1. Berechne die Größen
.
Das Verfahren lautet also im einzelnen: 1. Berechne die Größen
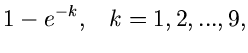
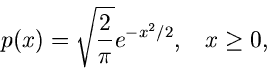
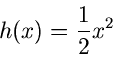

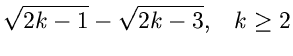
![$\displaystyle \frac{1}{2} x^{2}, \; \; \; \forall x \in [0,1],$](img358.gif)
![$\displaystyle \frac{1}{2} [x^{2} - 2k +3], \; \; \; \forall x \in
[\sqrt{2k-3}, \sqrt{2k-1} ], \; \; \; k \geq 2.$](img359.gif)
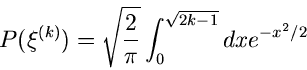
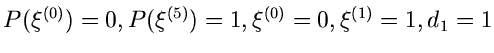 und berechne in einem externen
Programm
und berechne in einem externen
Programm
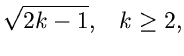
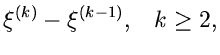


![\begin{displaymath}
u_{n-1} < \frac{1}{2} [\xi^{2} - 2 \kappa + 3] \leq u_{n}
\end{displaymath}](img369.gif)