Höhere Momente
Klassifizierung
Wir hatten im vorigen Unterkapitel vier spezielle erzeugende Funktionen
diskutiert, nämlich (im folgenden beschränken wir uns auf den eindimensionalen
Fall),
Hierbei haben wir die Abkürzung 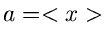 eingeführt, die wir in diesem
Unterkapitel beibehalten werden. Wir definierten die Momente mit Hilfe der
Ableitungen der erzeugenden Funktionen an der Stelle
eingeführt, die wir in diesem
Unterkapitel beibehalten werden. Wir definierten die Momente mit Hilfe der
Ableitungen der erzeugenden Funktionen an der Stelle 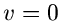 :
:
Man kann also, und hier liegt das Besondere dieser Darstellung für die
Simulation, eine Dichtefunktion 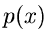 durch den vollständigen Satz von
Momenten irgendeiner der erzeugenden Funktionen beschreiben. Wenn z.B.
alle Momente
durch den vollständigen Satz von
Momenten irgendeiner der erzeugenden Funktionen beschreiben. Wenn z.B.
alle Momente
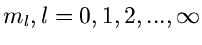 , gegeben sind, ist die
Dichtefunktion
, gegeben sind, ist die
Dichtefunktion 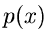 eindeutig bestimmt. Im folgenden werden wir noch
einige Formeln herleiten zur Umrechnung eines Satzes von Momenten in
irgendeinen der anderen Sätze (5) bis (8) von Momenten.
Hierzu benötigen wir die folgenden zwei grundlegenden Relationen zwischen
den erzeugenden Funktionen
eindeutig bestimmt. Im folgenden werden wir noch
einige Formeln herleiten zur Umrechnung eines Satzes von Momenten in
irgendeinen der anderen Sätze (5) bis (8) von Momenten.
Hierzu benötigen wir die folgenden zwei grundlegenden Relationen zwischen
den erzeugenden Funktionen
Normale und zentrale Momente
Wir benutzen die Gleichung (9),
Die erste und zweite Ableitungen lauten:
Für 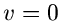 erhalten wir
erhalten wir
In diesen Formeln ist zu beachten, daß
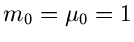 und
und
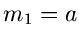 , sowie
, sowie 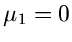 , daher
, daher
Mit Hilfe der höheren Ableitungen und vollständigen Induktion erhält man
die allgemeine Beziehung
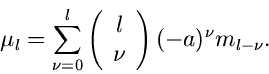 |
(14) |
In diesem Fall hätte man dasselbe Ergebnis auch einfacher erhalten
können durch Anwendung der Binominalformel auf die Beziehung
Die umgekehrte Relation ist genauso einfach und kann über die Ableitungen der
Relation
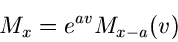 |
(15) |
bestimmt werden. In diesem Fall ist es jedoch ebenfalls einfacher, mit Hilfe
der Binominalformel und der Relation
zu arbeiten. Das Ergebnis ist
 |
(16) |
Für 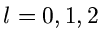 ergeben sich die ersten Momente zu
ergeben sich die ersten Momente zu
In diesen Formeln ist zu beachten, daß
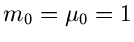 und
und
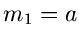 , sowie
, sowie 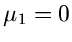 ist, daher
ist, daher
Normale und logarithmische Momente
Differenziert man die Definitionsgleichung (3),
so findet man
Für 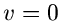 ergeben sich die ersten 3 Momente zu
ergeben sich die ersten 3 Momente zu
Durch Induktion erhält man leicht die allgemeine Beziehung
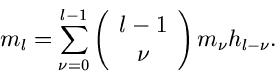 |
(20) |
Im Gegensatz zu (14) und (16) ist dieses eine Rekursions- Relation, da
auf der rechten Seite der Gleichung neben den Momenten 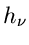 auch
die Momente
auch
die Momente 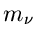 mit
mit
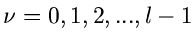 auftreten. Da
auftreten. Da  ist, kann man auch schreiben
ist, kann man auch schreiben
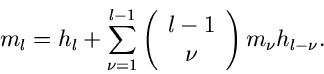 |
(21) |
Diese Formulierung gestattet es uns, die Umkehrung sofort hinzuschreiben,
nämlich
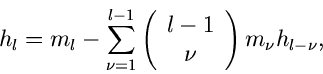 |
(22) |
oder, für die ersten 3 Momente,
Logarithmische und zentrale logarithmische Momente
Zur Umrechnung der normalen logarithmischen Momente in die zentralen
logarithmischen Momente benutzen wir die Relation (10),
Die Ableitungen sind trivial und ergeben
Daraus ergeben sich die Momente
Die normalen logarithmischen und zentralen logarithmischen Momente sind
also, bis auf 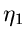 bzw
bzw 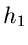 identisch gleich. Wir brauchen daher
auf die normalen logarithmischen Momente nicht weiter einzugehen.
identisch gleich. Wir brauchen daher
auf die normalen logarithmischen Momente nicht weiter einzugehen.
Zentrale und logarithmische Momente
Die zugrundeliegende Relation ist
Diese Beziehung ist, zumindest was die Ableitungen betrifft, vollkommen
equivalent zu
Daher können wir das Ergebnis sofort aus den Formeln (20) und (22) übernehmen,
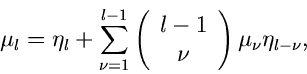 |
(23) |
und
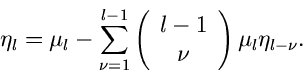 |
(24) |
Nachfolgend listen wir der Vollständigkeit halber die restlichen
Beziehungen zwischen den verschiedenen Momenten. Diese Relationen
können aus dem bisher gesagten ohne Schwierigkeiten hergeleitet werden.
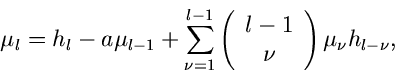 |
(25) |
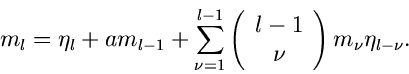 |
(26) |
Momente einer Summe unabhängiger Veränderlicher
Wir hatten bereits die Verteilungsfunktion einer Summe
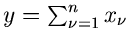 von unabhängigen Veränderlichen
von unabhängigen Veränderlichen  diskutiert. Für den Fall, daß die Dichtefunktionen aller Veränderlichen
diskutiert. Für den Fall, daß die Dichtefunktionen aller Veränderlichen
 gleich waren, fanden wir die Formel für die logarithmisch
erzeugende Funktion,
gleich waren, fanden wir die Formel für die logarithmisch
erzeugende Funktion,
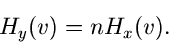 |
(27) |
Im Grenzfall 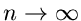 ergab sich, daß
ergab sich, daß 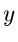 einer Normalverteilung
gehorcht, egal, welcher Verteilungsfunktion die unabhängigen
Veränderlichen
einer Normalverteilung
gehorcht, egal, welcher Verteilungsfunktion die unabhängigen
Veränderlichen  gehorchen. Außerdem hatten wir bei der
Diskussion der Faltung von Verteilungen bereits ein Verfahren angegeben,
wie man für beliebige Anzahlen
gehorchen. Außerdem hatten wir bei der
Diskussion der Faltung von Verteilungen bereits ein Verfahren angegeben,
wie man für beliebige Anzahlen 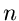 von unabhängigen Veränderlichen die
Verteilung der Summe
von unabhängigen Veränderlichen die
Verteilung der Summe 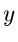 berechnen kann. Dieses ist jedoch (siehe (4.00))
ein relativ kompliziertes Integral. Ein eleganteres Verfahren soll in
diesem Absatz besprochen werden.
berechnen kann. Dieses ist jedoch (siehe (4.00))
ein relativ kompliziertes Integral. Ein eleganteres Verfahren soll in
diesem Absatz besprochen werden.
Um die Dichtefunktion 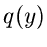 für verschiedene Anzahlen
für verschiedene Anzahlen 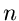 von
unabhängigen Veränderlichen
von
unabhängigen Veränderlichen
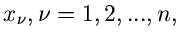 vergleichen zu
können, führen wir zunächst eine Variablen- Transformation durch,
vergleichen zu
können, führen wir zunächst eine Variablen- Transformation durch,
 |
(28) |
mit 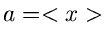 . Die Dichtefunktion von
. Die Dichtefunktion von 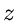 ist dann durch
ist dann durch
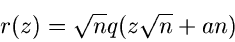 |
(29) |
gegeben. Die erzeugende Funktion von 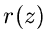 ist
ist
Wir führen wieder 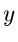 als Integrationsvariable ein und erhalten
als Integrationsvariable ein und erhalten
Damit erhalten wir eine Beziehung zwischen den erzeugenden Funktionen von
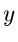 und
und 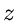 :
:
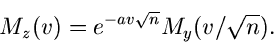 |
(30) |
Diese Gleichung kann man linearisieren, indem wir zur logarithmisch
erzeugenden Funktion übergehen,
Im letzten Schritt sind wir noch von der erzeugenden Funktion von 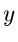 auf
die erzeugende Funktion von
auf
die erzeugende Funktion von 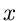 übergegangen. Die Ableitungen dieser
letzten Gleichung ergeben
übergegangen. Die Ableitungen dieser
letzten Gleichung ergeben
Bezeichnen wir mit 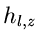 und
und  die logarithmischen Momente von
die logarithmischen Momente von
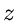 und
und 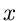 , so ergibt sich
, so ergibt sich
Für 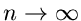 verschwinden also alle logarithmischen Momente
verschwinden also alle logarithmischen Momente
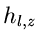 mit
mit 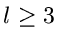 der Veränderlichen
der Veränderlichen 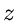 . Das einzige
nichtverschwindende Moment ist
. Das einzige
nichtverschwindende Moment ist
Die logarithmisch erzeugende Funktion ist für 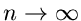
und die erzeugende Funktion
woraus man sofort die Verteilungsfunktion 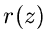 von
von 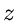 ablesen kann,
ablesen kann,
![\begin{displaymath}
r(z) = \frac{1}{\sqrt{2 \pi} \sigma_{y}} e^{-z^{2}/[2 \sigma_{y}^{2}]}.
\end{displaymath}](img123.gif) |
(31) |
Wir möchten in diesem Zusammenhang aber ausdrücklich darauf hinweisen,
daß man nur im Grenzfall 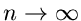 eine Normalverteilung erhält.
Für endliche Werte von
eine Normalverteilung erhält.
Für endliche Werte von 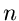 muß der Fehler, den man bei Vernachlässigung
der logarithmischen Momente mit
muß der Fehler, den man bei Vernachlässigung
der logarithmischen Momente mit 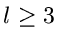 macht, genau abgeschätzt
werden.
macht, genau abgeschätzt
werden.
Faltung unabhängiger Gleichverteilungen
Als Beispiel diskutieren wir die Summe von 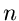 Veränderlichen
Veränderlichen
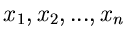 aus Gleichverteilungen im Intervall
aus Gleichverteilungen im Intervall
![$[-\frac{1}{2}, + \frac{1}{2}]$](img125.gif) . Die Dichtefunktionen lauten
. Die Dichtefunktionen lauten
Die Erwartungswerte sind offensichtlich
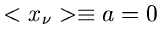 .
Gesucht sind daher die Dichtefunktionen der Veränderlichen
.
Gesucht sind daher die Dichtefunktionen der Veränderlichen
bzw.
Die erzeugende Funktion der Veränderlichen 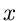 ist
ist
 |
(32) |
Wir hatten die folgende Beziehung zwischen den logarithmisch
erzeugenden Funktionen von 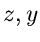 und
und 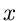 :
:
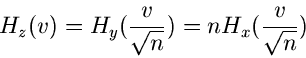 |
(33) |
Wir könnten jetzt die Ableitungen rechnen und die logarithmischen
Momente von 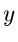 und
und 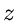 bestimmen. In diesem Fall sind die Ableitungen
jedoch ziemlich kompliziert. Wir gehen daher anders vor und bestimmen
zunächst die Momente der Veränderlichen
bestimmen. In diesem Fall sind die Ableitungen
jedoch ziemlich kompliziert. Wir gehen daher anders vor und bestimmen
zunächst die Momente der Veränderlichen 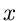 . Aus
. Aus
und der Rekursionsrelation (22),
ergibt sich der Reihe nach für die ersten 4 Momente
Wir können also ohne großen Fehler setzen:
Daher ist
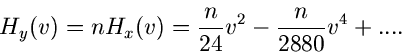 |
(34) |
und
Simulation der Normalverteilung
Auf diesem Ergebnis aufbauend erschließt sich uns eine sehr einfache
Simulation der Normalverteilung. Die höheren Momente von 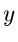 und
und 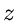 sind
außerordentlich klein, außer für
sind
außerordentlich klein, außer für 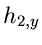 und
und 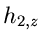 ,
,
Generiert man also 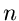 gleichverteilte Zufallszahlen aus dem Intervall
gleichverteilte Zufallszahlen aus dem Intervall
![$[-\frac{1}{2}, + \frac{1}{2}]$](img125.gif) und bildet die Summe
und bildet die Summe
so ist 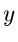 näherungsweise normalverteilt mit dem Erwartungswert
näherungsweise normalverteilt mit dem Erwartungswert
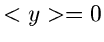 und der Varianz
und der Varianz
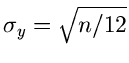 . Wählt man also
. Wählt man also
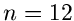 , so erhält man eine Normalverteilung mit der Varianz
, so erhält man eine Normalverteilung mit der Varianz  .
.
Harm Fesefeldt
2006-05-08
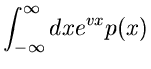
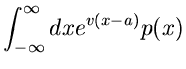
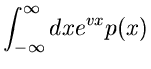
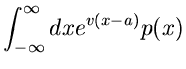
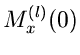
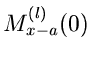
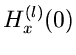
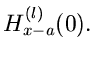

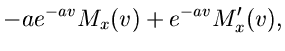
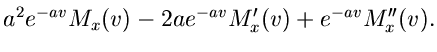
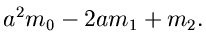
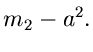
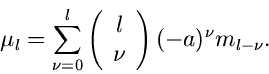

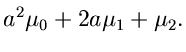
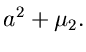
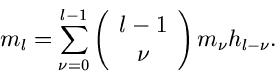
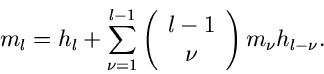
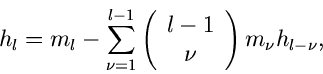
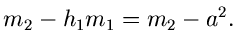
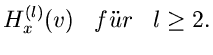
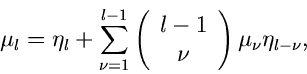
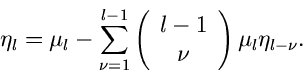
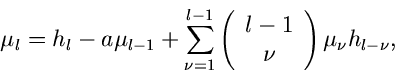
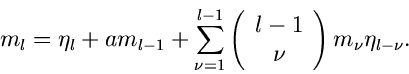
![]() von unabhängigen Veränderlichen
von unabhängigen Veränderlichen ![]() diskutiert. Für den Fall, daß die Dichtefunktionen aller Veränderlichen
diskutiert. Für den Fall, daß die Dichtefunktionen aller Veränderlichen
![]() gleich waren, fanden wir die Formel für die logarithmisch
erzeugende Funktion,
gleich waren, fanden wir die Formel für die logarithmisch
erzeugende Funktion,
![]() für verschiedene Anzahlen
für verschiedene Anzahlen ![]() von
unabhängigen Veränderlichen
von
unabhängigen Veränderlichen
![]() vergleichen zu
können, führen wir zunächst eine Variablen- Transformation durch,
vergleichen zu
können, führen wir zunächst eine Variablen- Transformation durch,

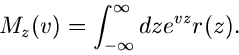

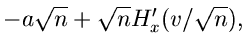
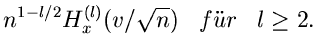
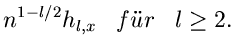
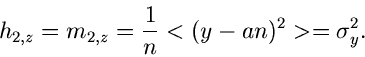
![\begin{displaymath}
r(z) = \frac{1}{\sqrt{2 \pi} \sigma_{y}} e^{-z^{2}/[2 \sigma_{y}^{2}]}.
\end{displaymath}](img123.gif)
![]() Veränderlichen
Veränderlichen
![]() aus Gleichverteilungen im Intervall
aus Gleichverteilungen im Intervall
![$[-\frac{1}{2}, + \frac{1}{2}]$](img125.gif) . Die Dichtefunktionen lauten
. Die Dichtefunktionen lauten
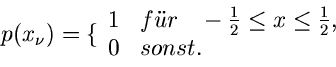
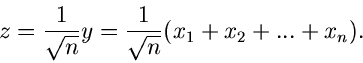

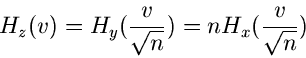
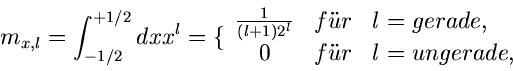
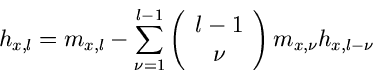
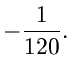
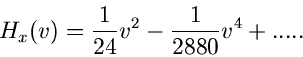
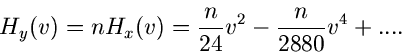
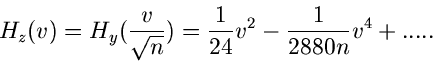
![]() und
und ![]() sind
außerordentlich klein, außer für
sind
außerordentlich klein, außer für ![]() und
und ![]() ,
,
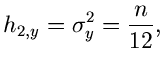
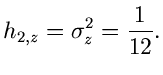
![$[-\frac{1}{2}, + \frac{1}{2}]$](img125.gif) und bildet die Summe
und bildet die Summe
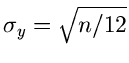 . Wählt man also
. Wählt man also