Erzeugende Funktionen
Definitionen
Wir hatten in einem früheren Teil dieses Tutorials bereits die Erwartungswerte von irgendwelchen Potenzen
der zufälligen Veränderlichen
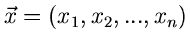 definiert,
und zwar
definiert,
und zwar
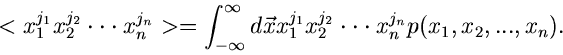 |
(1) |
Ähnlich wurden die zentralen Momente definiert. Diese
Definitionen lassen sich weiter verallgemeinern. Sei 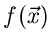 irgendeine
Funktion des Vektors
irgendeine
Funktion des Vektors 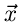 , so definieren wir den verallgemeinerten
Erwartungswert der Größe
, so definieren wir den verallgemeinerten
Erwartungswert der Größe 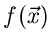 in der Verteilung
in der Verteilung 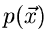 als
als
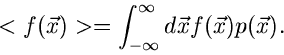 |
(2) |
Diese Definition schließt den oben angegebenen Erwartungswert mit
offensichtlich ein.
Wir definieren jetzt die allgemeine erzeugende Funktion durch
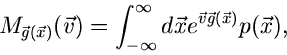 |
(3) |
wobei
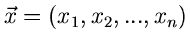 ein zufälliger Vektor der Dimension
ein zufälliger Vektor der Dimension
 ,
,
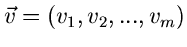 und
und
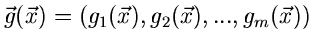 komplexe oder reelle Vektoren der Dimension
komplexe oder reelle Vektoren der Dimension 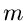 sind. Die Dimensionen von
sind. Die Dimensionen von
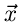 und
und 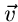 bzw
bzw 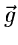 brauchen insbesondere nicht
übereinzustimmen. Man schreibt die Funktion
brauchen insbesondere nicht
übereinzustimmen. Man schreibt die Funktion
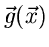 , mit deren
Hilfe die erzeugende Funktion definiert wird, als unteren Index an das
Funktionssymbol
, mit deren
Hilfe die erzeugende Funktion definiert wird, als unteren Index an das
Funktionssymbol 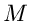 . Ein Vergleich der Formeln (2) und (3) zeigt, daß
. Ein Vergleich der Formeln (2) und (3) zeigt, daß
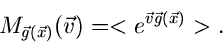 |
(4) |
Entwickelt man die Exponentialfunktion in eine Reihe, so folgt sofort
die wichtige Formel
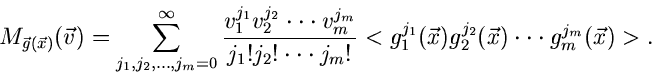 |
(5) |
Die erzeugende Funktion kann als Reihenentwicklung dargestellt werden,
deren Entwicklungskoeffizienten die Momente der Funktionen
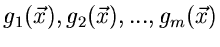 sind. Man nennt
sind. Man nennt
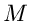 daher auch häufig die Moment- erzeugende Funktion.
In dieser wohl allgemeinsten Form verwendet man die erzeugenden Funktionen
allerdings selten.
daher auch häufig die Moment- erzeugende Funktion.
In dieser wohl allgemeinsten Form verwendet man die erzeugenden Funktionen
allerdings selten.
Klassifizierung
In den Anwendungen hat man es vorzugsweise mit den folgenden erzeugenden
Funktionen zu tun. Die Bezeichnungen sind in der Literatur nicht immer
eindeutig. Man muß daher immer auf die exakte mathematische Definition
zurückgehen.
1. Erzeugende Funktion im engeren Sinne
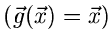 :
:
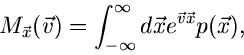 |
(6) |
wobei 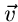 ein Vektor komplexer Zahlen ist. Diese Funktionaltransformation
ist, bis auf das Vorzeichen im Exponenten, identisch mit der (zweiseitigen)
Laplace- Transformation.
ein Vektor komplexer Zahlen ist. Diese Funktionaltransformation
ist, bis auf das Vorzeichen im Exponenten, identisch mit der (zweiseitigen)
Laplace- Transformation.
2. Charakteristische Funktion
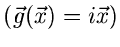 :
:
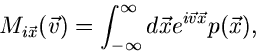 |
(7) |
wobei 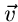 ein Vektor reeller Zahlen ist. Es ist unschwer zu erkennen,
daß diese Funktionaltransformation, bis auf das Vorzeichen im Exponenten,
die Fourier- Transformierte der Dichtefunktion
ein Vektor reeller Zahlen ist. Es ist unschwer zu erkennen,
daß diese Funktionaltransformation, bis auf das Vorzeichen im Exponenten,
die Fourier- Transformierte der Dichtefunktion 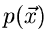 ist.
ist.
3. Zentrale erzeugende Funktion
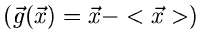 :
:
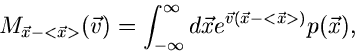 |
(8) |
wobei
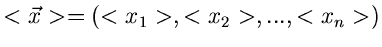 der Erwartungswert des
zufälligen Vektors
der Erwartungswert des
zufälligen Vektors 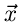 ist. Da
ist. Da 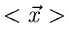 eine Konstante im Integral
ist, kann
eine Konstante im Integral
ist, kann
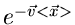 vor das Integralzeichen gezogen werden,
sodaß man die wichtige Beziehung zwischen der normalen erzeugenden
Funktion und der zentralen erzeugenden Funktion,
vor das Integralzeichen gezogen werden,
sodaß man die wichtige Beziehung zwischen der normalen erzeugenden
Funktion und der zentralen erzeugenden Funktion,
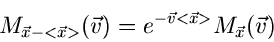 |
(9) |
erhält. Die Umkehrung dieser Beziehung lautet
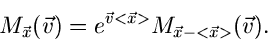 |
(10) |
4. Zentrale charakteristische Funktion
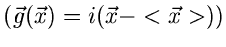 :
:
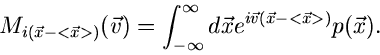 |
(11) |
Auch hier kann man leicht die Verbindung mit der normalen charakteristischen
Funktion herstellen:
 |
(12) |
Die Umkehrung lautet
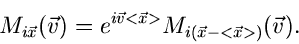 |
(13) |
Für alle vier soeben definierten Funktionaltransformationen kann die
Reihenentwicklung in der Form (siehe auch (5))
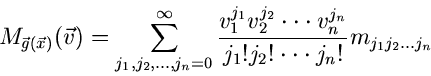 |
(14) |
geschrieben werden, mit den Momenten
1.
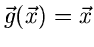 :
:
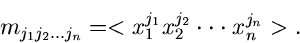 |
(15) |
2.
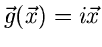 :
:
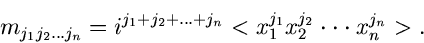 |
(16) |
3.
 :
:
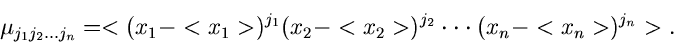 |
(17) |
4.
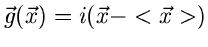 :
:
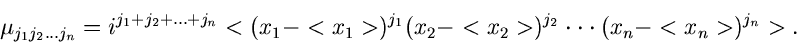 |
(18) |
Die unter Punkt 3 und 4 aufgeführten zentralen Momente bezeichnen wir
im folgenden mit
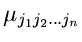 statt mit
statt mit
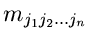 .
Aus den Reihenentwicklungen ersieht man insbesondere, daß für die
Laplace Transformierte
.
Aus den Reihenentwicklungen ersieht man insbesondere, daß für die
Laplace Transformierte
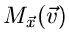 gilt
gilt
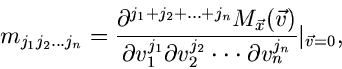 |
(19) |
sowie für die Fourier- Transformierte
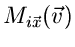 :
:
 |
(20) |
Ähnliche Ausdrücke kann man für die zentralen Momente hinschreiben.
Im folgenden werden wir mit den erzeugenden und zentralen erzeugenden
Funktionen arbeiten. Es ist nicht schwierig, die Formulierung einer
Aufgabe mit Hilfe der charakteristischen Funktion durchzuführen.
Dieses überlassen wir dem Leser. Auch könnten wir die normale
Laplace- Transformation
oder die normale Fourier- Transformation
benutzen. Bis auf Faktoren 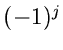 ergibt sich dasselbe wie bei den
erzeugenden und charakteristischen Funktionen.
ergibt sich dasselbe wie bei den
erzeugenden und charakteristischen Funktionen.
Als letztes bemerken wir noch, daß im Falle einer diskreten Veränderlichen
 mit der Wahrscheinlichkeitsverteilung
mit der Wahrscheinlichkeitsverteilung
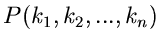 alle Formeln und Definitionen erhalten bleiben,
sofern man das Integralzeichen durch ein Summenzeichen ersetzt:
alle Formeln und Definitionen erhalten bleiben,
sofern man das Integralzeichen durch ein Summenzeichen ersetzt:
 |
(21) |
Beispiel.
Die Gleichverteilung im Intervall ![$[0,1]$](img56.gif) ,
,
hat die erzeugende Funktion
und die zentrale erzeugende Funktion
Man beachte, daß, obwohl  nur im Intervall
nur im Intervall ![$[0,1]$](img56.gif) gegeben war, die
erzeugende Funktion in der gesamten komplexen Zahlenebene definiert ist.
gegeben war, die
erzeugende Funktion in der gesamten komplexen Zahlenebene definiert ist.
Beispiel.
Die allgemeine eindimensionale Normalverteilung
hat die erzeugende Funktion
und die zentrale erzeugende Funktion
Dieses Ergebnis läßt sich relativ einfach auf die  -dimensionale
Normalverteilung verallgemeinern. Wir schreiben sie in der Form
-dimensionale
Normalverteilung verallgemeinern. Wir schreiben sie in der Form
mit
Hierbei sind die Erwartungswerte und die Kovarianzmatrix durch
gegeben. Alle höheren Momente sind identisch gleich Null. Man beachte,
daß im Exponenten der Verteilung die Elemente der inversen Kovarianzmatrix
stehen. Man kann nun leicht zeigen, daß die zentrale erzeugende
Funktion durch
gegeben ist. Dazu bilden wir die partiellen Ableitungen und beachten, daß
sein sollte. Vergleich mit den oben angegebenen Erwartungswerten und
den Elementen der Kovarianzmatrix ergibt den Beweis. Die normale erzeugende
Funktion ist
Beispiel.
Für die Exponentialverteilung
erhält man
Dieses Integral ist nur für
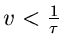 lösbar und ergibt
lösbar und ergibt
Die zentrale erzeugende Funktion wird daher
Eine Verallgemeinerung der Exponentialverteilung ist die 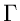 -
Verteilung,
-
Verteilung,
Die Exponentialverteilung folgt hieraus als Spezialfall für 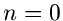 .
Durch Integration erhält man die erzeugende Funktion zu
.
Durch Integration erhält man die erzeugende Funktion zu
Das Maximum der 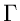 - Verteilungt liegt an der Stelle
- Verteilungt liegt an der Stelle 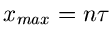 .
Wir entwickeln den Logarithmus der
.
Wir entwickeln den Logarithmus der 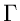 - Verteilung in eine Reihe.
Für
- Verteilung in eine Reihe.
Für
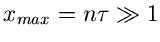 erhält man die Näherung
erhält man die Näherung
Für 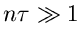 kann die
kann die 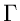 - Verteilung also durch eine
Normalverteilung mit Mittelwert
- Verteilung also durch eine
Normalverteilung mit Mittelwert 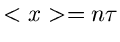 und Varianz
und Varianz
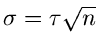 approximiert werden.
approximiert werden.
Beispiel.
Die Bernoulli- Verteilung
hat die erzeugende Funktion
und die zentrale erzeugende Funktion
Beispiel.
Als letztes Beispiel geben wir noch die erzeugende Funktion der Poisson-
Verteilung. Aus
folgt
und
Summe unabhängiger Veränderlicher
Gegeben sei die  -dimensionale Veränderliche
-dimensionale Veränderliche
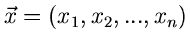 mit der Dichtefunktion
mit der Dichtefunktion
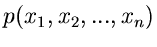 . Seien alle
. Seien alle  Veränderliche unabhängig
voneinander, d.h.
Veränderliche unabhängig
voneinander, d.h.
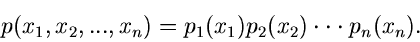 |
(22) |
Wir definieren nun eine neue Veränderliche 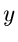 durch die Summe der
durch die Summe der
 Veränderlichen
Veränderlichen 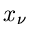 ,
,
 |
(23) |
Die Veränderliche 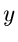 soll durch die Dichtefunktion
soll durch die Dichtefunktion 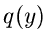 beschrieben
werden. Die Aufgabe ist nun, diese Dichtefunktion
beschrieben
werden. Die Aufgabe ist nun, diese Dichtefunktion 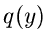 zu bestimmen.
zu bestimmen.
Wir stellen zunächst fest, daß die erzeugende Funktion von 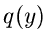 durch
durch
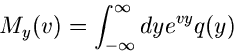 |
(24) |
gegeben ist. Dieses ist aber nichts anderes als der Erwartungswert
d.h.
Benutzen wir jetzt die Annahme (22) über die Unabhängigkeit der
Veränderlichen
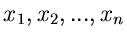 , so folgt
, so folgt
oder
 |
(25) |
mit
Wir fassen diesen Sachverhalt in einem Satz zusammen: Die erzeugende
Funktion einer Summe unabhängiger Veränderlicher ist gleich dem Produkt
der erzeugenden Funktionen der einzelnen unabhängigen Veränderlichen.
Logarithmisch erzeugende Funktion
In diesem Zusammenhang definiert man nun häufig eine weitere erzeugende
Funktion, nämlich die logarithmisch erzeugende Funktion
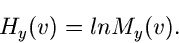 |
(26) |
Anwendung auf Formel (25) liefert
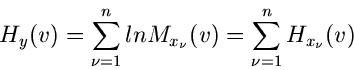 |
(27) |
mit
Der Grund für die Einführung der logarithmisch erzeugenden Funktion ist
natürlich, daß man eine Summe von Funktionen mathematisch wesentlich
einfacher handhaben kann als ein Produkt.
Beispiele.
Ein weiterer wichtiger Grund für die Einführung der logarithmisch
erzeugenden Funktion ist, daß viele erzeugende Funktion mit Hilfe von
Exponentialfunktionen darstellbar sind, die logarithmisch erzeugende
Funktion daher aus dem Exponenten gebildet wird. So ist z.B. die
logarithmisch erzeugende Funktion der allgemeinen Normalverteilung
durch
und die logarithmisch erzeugende Funktion der Poisson- Verteilung,
durch
gegeben. Auch in anderen Fällen kann man wesentliche Vereinfachungen
durch Einführung der logarithmisch erzeugenden Funktionen erhalten.
Die Bernoulli- Verteilung
bezitzt die logarithmisch erzeugende Funktion
und die zentrale logarithmisch erzeugende Funktion
Für die  - Verteilung
- Verteilung
erhalten wir ähnlich
Ein Vorteil dieser Darstellung ist, daß einfache Reihenentwicklungen
möglich sind. Mit Hilfe der Formeln
ergibt sich z.B. für die  - Verteilung
- Verteilung
Hieraus sieht man sofort, daß die 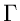 - Verteilung durch eine
Normalverteilung mit Mittelwert
- Verteilung durch eine
Normalverteilung mit Mittelwert 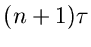 und Varianz
und Varianz
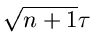 approximiert werden kann. Für
approximiert werden kann. Für 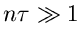 kann man
die 1 gegenüber
kann man
die 1 gegenüber  vernachlässigen und erhält das bereits oben
hergeleitete Ergebnis für die Normalverteilung.
vernachlässigen und erhält das bereits oben
hergeleitete Ergebnis für die Normalverteilung.
Unabhängige Veränderliche mit gleichen Dichtefunktionen
Haben alle Veränderliche 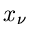 die gleiche Dichtefunktion, d.h. wenn
die gleiche Dichtefunktion, d.h. wenn
 |
(28) |
dann ist auch
und wir können (25) einfacher schreiben als
oder
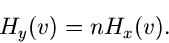 |
(29) |
Wie wir oben ausgeführt haben, kann 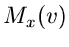 in eine Reihe um
in eine Reihe um 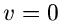 entwickelt werden,
entwickelt werden,
mit
Diese Reihe approximieren wir durch
Die logarithmisch erzeugende Funktion wird dann zu
oder
 |
(30) |
In dieser Herleitung wurde angenommen, daß alle Terme mit 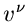 ,
,
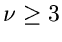 , als klein betrachtet und daher vernachlässigt werden
können. Diese Annahme und insbesondere den Geltungsbereich dieser
Annahme werden wir mathematisch exakt später behandeln. Für die
erzeugende Funktion erhalten wir
, als klein betrachtet und daher vernachlässigt werden
können. Diese Annahme und insbesondere den Geltungsbereich dieser
Annahme werden wir mathematisch exakt später behandeln. Für die
erzeugende Funktion erhalten wir
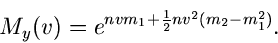 |
(31) |
Die Rücktransformation ergibt
![\begin{displaymath}
q(y) = \frac{1}{\sqrt{2 \pi n (m_{2}-m_{1}^{2})}}
e^{-(x-n m_{1})^{2}/[2n (m_{2}-m_{1}^{2})]}.
\end{displaymath}](img143.gif) |
(32) |
Wir formulieren die wesentliche Aussage dieser Formel in einem Satz:
Eine Summe
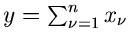 unabhängiger Veränderlicher
unabhängiger Veränderlicher
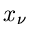 mit gleichen Dichtefunktionen
mit gleichen Dichtefunktionen 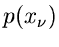 ist näherungsweise
normal verteilt mit dem Mittelwert
ist näherungsweise
normal verteilt mit dem Mittelwert
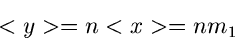 |
(33) |
und der Standardabweichung
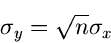 |
(34) |
mit
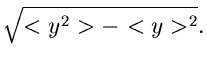
Die approximative Formel für die Dichtefunktion lautet
![\begin{displaymath}
q(y) = \frac{1}{\sqrt{2 \pi} \sigma_{y}} e^{-(y-<y>)^{2}/[2 \sigma_{y}^{2}]}.
\end{displaymath}](img152.gif) |
(37) |
Man beachte, daß die Einzelverteilungen der Veränderlichen 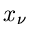 nicht normal verteilt zu sein brauchen.
nicht normal verteilt zu sein brauchen.
Wir sind den Beweis schuldig geblieben, daß Formel (32) für 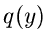 wirklich die Rücktransformierte der erzeugenden Funktion (31) ist.
Man kann diese Behauptung natürlich durch Einsetzen von
wirklich die Rücktransformierte der erzeugenden Funktion (31) ist.
Man kann diese Behauptung natürlich durch Einsetzen von 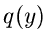 in die
Definitionsgleichung (6) der erzeugenden Funktion und explizites
Lösen des Integrals zeigen. Auf ein allgemeines Verfahren zur
Rücktransformation werden wir später eingehen.
in die
Definitionsgleichung (6) der erzeugenden Funktion und explizites
Lösen des Integrals zeigen. Auf ein allgemeines Verfahren zur
Rücktransformation werden wir später eingehen.
Faltung von Verteilungen
Was wir soeben für den Spezialfall einer großen Anzahl
unabhängiger Veränderlicher
durchgerechnet haben, ist nichts anderes als eine sogenannte Faltung
von Verteilungen. Hierauf werden wir im folgenden noch etwas näher
eingehen. Die anschauliche Bedeutung der Faltung ersieht man einfachsten
für diskrete Veränderliche. Seien also 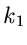 und
und 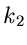 zwei
unabhängige Veränderliche mit den Wahrscheinlichkeitsverteilungen
zwei
unabhängige Veränderliche mit den Wahrscheinlichkeitsverteilungen
 und
und  . Mißt man beide Veränderliche
gleichzeitig, so ist wegen der Annahme der Unabhängigkeit die
zweidimensionale Verteilung durch
. Mißt man beide Veränderliche
gleichzeitig, so ist wegen der Annahme der Unabhängigkeit die
zweidimensionale Verteilung durch
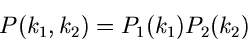 |
(38) |
gegeben. Die Frage ist nun, welcher Verteilungsfunktion die neue
Veränderliche  gehorcht. Man schreibt dafür häufig
gehorcht. Man schreibt dafür häufig
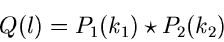 |
(39) |
und nennt diesen Ausdruck die Faltung der unabhängigen zufälligen
Veränderlichen 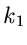 und
und 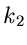 . Der Stern zwischen den
Verteilungsfunktionen
. Der Stern zwischen den
Verteilungsfunktionen 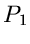 und
und 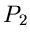 soll die mathematische Operation
andeuten, die man durchzuführen hat, um aus den beiden Verteilungen
soll die mathematische Operation
andeuten, die man durchzuführen hat, um aus den beiden Verteilungen
 und
und  die neue Verteilung
die neue Verteilung  zu erhalten.
Dieses Symbol hat insbesondere nichts mit einer algebraischen Multiplikation
zu tun. Wir nehmen im folgenden an, daß die diskreten Veränderlichen
zu erhalten.
Dieses Symbol hat insbesondere nichts mit einer algebraischen Multiplikation
zu tun. Wir nehmen im folgenden an, daß die diskreten Veränderlichen
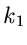 und
und 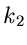 auf positive Werte beschränkt sind.
auf positive Werte beschränkt sind.
Die Veränderliche  ist dann und nur dann null, wenn
ist dann und nur dann null, wenn 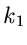 und
und
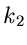 gleichzeitig null sind, daher
gleichzeitig null sind, daher
Den Wert 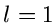 erhält man zweimal, und zwar für
erhält man zweimal, und zwar für
Daraus schließen wir
Ausdrücke dieser Art erhält man nun für jeden Wert von  ,
,
oder
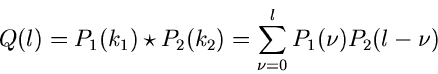 |
(40) |
Diese Formel läßt sich einfach auf kontinuierliche Veränderliche
übertragen:
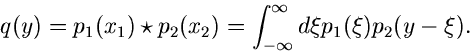 |
(41) |
Den Ausdruck (40) kann man auch folgendermaßen schreiben:
In dieser Form läßt sich die Faltung von Verteilungen leicht auf mehrere
unabhängige Veränderliche verallgemeinern, nämlich
 |
(42) |
Für kontinuierliche Veränderliche erhält man die Verallgemeinerung
auf  Veränderliche am einfachsten aus (42):
Veränderliche am einfachsten aus (42):
Wendet man nun auf den Ausdruck (43) die Laplace- Transformation an,
so kommt man, wie es natürlich auch sein muß, wieder auf die Formel
(25) für die erzeugende Funktion einer Summe
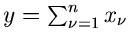 unabhängiger Veränderlicher
unabhängiger Veränderlicher 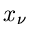 :
:
Wir führen die Variable
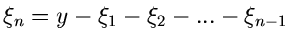 ein
und erhalten
ein
und erhalten
Dieses ist offensichtlich identisch mit dem Ausdruck (25).
Beispiel.
In der Praxis kommt es häufig vor, daß eine zufällige Veränderliche
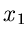 mit der Dichtefunktion
mit der Dichtefunktion 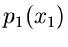 mit einem normalverteilten
Meßfehler
mit einem normalverteilten
Meßfehler 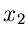 ,
,
gefaltet werden muß. Das Ergebnis einer Messung ist dann die Summe
Die zu erwartende Dichtefunktion 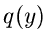 ist als Integral darstellbar:
ist als Integral darstellbar:
Die Lösung dieses Integrals ist für die meisten Dichtefunktionen
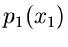 außerordentlich mühsam. Wir bedienen uns daher der
erzeugenden Funktionen. Die logarithmisch erzeugende Funktion der
Normalverteilung
außerordentlich mühsam. Wir bedienen uns daher der
erzeugenden Funktionen. Die logarithmisch erzeugende Funktion der
Normalverteilung
muß zur logarithmisch erzeugenden Funktion  der Dichtefunktion
der Dichtefunktion
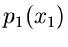 addiert werden,
addiert werden,
Ist 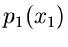 ebenfalls eine Normalverteilung,
ebenfalls eine Normalverteilung,
so folgt
und die resultierende Dichtefunktion lautet
Um zu diesem einfachen Ergebnis zu kommen, hätten wir bei der Auswertung
des obigen Integrals einige Seiten rechnen müssen.
Für irgendeine andere Verteilung 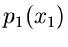 anstatt der Normalverteilung
ist die Faltung im Prinzip ebenso einfach, jedoch hätten wir bei der
Rücktransformation von der erzeugenden Funktion zur Dichtefunktion einige
Probleme. Ein allgemeines Verfahren hierzu werden wir erst im nächsten Abschnitt
angeben.
anstatt der Normalverteilung
ist die Faltung im Prinzip ebenso einfach, jedoch hätten wir bei der
Rücktransformation von der erzeugenden Funktion zur Dichtefunktion einige
Probleme. Ein allgemeines Verfahren hierzu werden wir erst im nächsten Abschnitt
angeben.
Laurent- Transformation für diskrete Veränderliche
Eine von den bisher erklärten erzeugenden Funktionen abweichende
Definition gibt es noch für diskrete Veränderliche. Die bis auf das
Vorzeichen im Exponenten mit der Laurent- Transformation (bzw
Z- Transformation) identische Funktionaltransformation
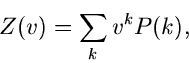 |
(44) |
erfüllt die wichtige Relation
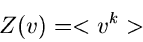 |
(45) |
und hat in den Anwendungen eine mindestens ebenso große Bedeutung wie
die Laplace- oder Fourier- Transformationen diskreter Veränderlicher,
Die  -fache Ableitung nach
-fache Ableitung nach 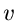 führt auf
führt auf
Für 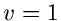 erhalten wir
erhalten wir
 |
(48) |
und insbesondere für 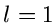 und
und 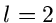 :
:
Daraus ergibt sich das zweite Moment
Für die Laurent- Transformierte gilt der wichtige Satz: Seien
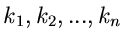 unabhängige Veränderliche mit den
Wahrscheinlichkeitsverteilungen
unabhängige Veränderliche mit den
Wahrscheinlichkeitsverteilungen
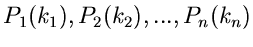 und den Laurent- Transformierten
und den Laurent- Transformierten
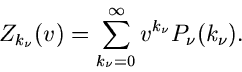 |
(49) |
Dann hat die Wahrscheinlichkeitsverteilung der Summe der  Veränderlichen
Veränderlichen
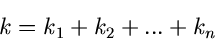 |
(50) |
die Laurent- Transformierte
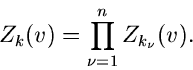 |
(51) |
Beispiel.
Als Beispiel zur Laurent Transformation rechnen wir die Faltung zweier
Poisson Verteilungen,
Die Laurent Transformierten sind
Unter der Annahme, daß 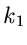 und
und 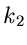 unabhängige Veränderliche sind,
ist die Laurent Transformierte der Summe
unabhängige Veränderliche sind,
ist die Laurent Transformierte der Summe
das Produkt der Laurent Transformierten der Einzelverteilungen:
Die resultierende Dichtefunktion
ist wieder eine Poisson Verteilung, allerdings mit Parameter 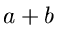 .
.
Beispiel.
Zur Vorbereitung auf das nächste Beispiel diskutieren wir zunächst
noch einmal eine Herleitung für die Bernoulli Verteilung. In einführenden Teil dieses Tutorials
hatten wir bereits eine Herleitung der Bernoulli Verteilung mit Hilfe der
vollständigen Induktion angegeben. Hier nun wollen wir eine Herleitung
mit Hilfe von erzeugenden Funktionen diskutieren.
Ein Experiment möge als Ergebnis nur zwei mögliche Ereignisse,
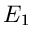 und
und 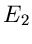 , besitzen.
, besitzen. 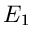 und
und 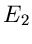 seien Elementarereignisse,
seien Elementarereignisse,
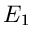 als Ergebnis schließt das Ereignis
als Ergebnis schließt das Ereignis 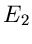 also aus und umgekehrt
schließt
also aus und umgekehrt
schließt 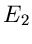 das Ereignis
das Ereignis 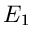 aus. Wir ordnen den Ereignissen
aus. Wir ordnen den Ereignissen
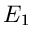 und
und 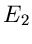 die zufälligen Veränderlichen
die zufälligen Veränderlichen 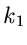 und
und 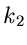 zu und definieren
zu und definieren
Die Ereignisse 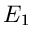 und
und 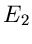 mögen mit den Wahrscheinlichkeiten
mögen mit den Wahrscheinlichkeiten
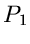 und
und 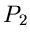 auftreten. Da eines der beiden Ereignisse immer
eintreten muß, haben wir in diesem Problem nur eine zufällige
Veränderliche, die andere ist vollständig determiniert. Wir wählen
auftreten. Da eines der beiden Ereignisse immer
eintreten muß, haben wir in diesem Problem nur eine zufällige
Veränderliche, die andere ist vollständig determiniert. Wir wählen
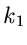 als zufällige Veränderliche. Dann gilt:
als zufällige Veränderliche. Dann gilt:
Die Wahrscheinlichkeitsverteilung für 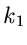 besitzt also nur die
zwei Werte
besitzt also nur die
zwei Werte
Die Laurent- Transformierte dieser Verteilung ist
Wir führen die Messung der Veränderlichen 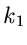 jetzt
jetzt 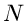 - mal
durch und erhalten die Ergebnisse
- mal
durch und erhalten die Ergebnisse
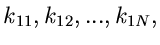 alle mit
den Werten 0 oder 1. Die Summe
alle mit
den Werten 0 oder 1. Die Summe
gibt dann an, wie oft das Ereignis 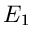 bei
bei 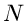 - maliger Ausführung
des Versuches aufgetreten ist. Die Laurent- Transformierte von
- maliger Ausführung
des Versuches aufgetreten ist. Die Laurent- Transformierte von 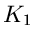 ist
ist
Dieses ist aber nichts anderes als die Laurent- Transformierte der
Bernoulli- Verteilung
Hiervon überzeugt man sich leicht durch explizites Rechnen:
Für das nachfolgende Beispiel schreiben wir die Bernoulli- Verteilung
in einer etwas anderen Form,
mit
und
Man beachte bei dieser Schreibweise aber, daß 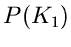 nur von der
einen Veränderlichen
nur von der
einen Veränderlichen 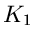 abhängt.
abhängt.
Beispiel.
Das vorige Beispiel läßt sich dahingehend verallgemeinern, daß der
Versuch 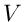 zu
zu 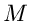 verschiedenen Elementarereignissen
verschiedenen Elementarereignissen
 führen kann. Wir definieren den diskreten Vektor
führen kann. Wir definieren den diskreten Vektor
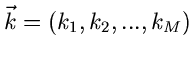 durch die Zuordnung
durch die Zuordnung
Die Wahrscheinlichkeitsverteilung ist offenbar
wobei wir deutlich gemacht haben, daß diese Verteilung nur von 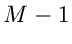 Veränderlichen abhängt, die
Veränderlichen abhängt, die 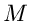 - te Komponente ist bei Angabe der
ersten
- te Komponente ist bei Angabe der
ersten 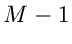 Komponenten vollständig determiniert:
Komponenten vollständig determiniert:
Darüber hinaus
besteht noch eine weitere starke Korrelation zwischen den Komponenten
des Vektors 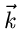 : wenn eine Komponente
: wenn eine Komponente 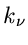 den Wert 1 hat,
müssen notwendigerweise alle anderen Komponenten den Wert 0 haben.
den Wert 1 hat,
müssen notwendigerweise alle anderen Komponenten den Wert 0 haben.
Die Laurent Transformierte dieser Verteilung ist
Wir messen wie immer den Vektor 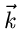 in
in 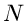 unabhängigen Versuchen,
mit den Ergebnissen
unabhängigen Versuchen,
mit den Ergebnissen
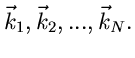 Die einzelnen Komponenten des Summenvektors
Die einzelnen Komponenten des Summenvektors
geben dann an, wie häufig in 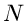 Versuchen die Elementarereignisse
Versuchen die Elementarereignisse
 aufgetreten sind. Die Laurent- Transformierte
der Wahrscheinlichkeitsverteilung von
aufgetreten sind. Die Laurent- Transformierte
der Wahrscheinlichkeitsverteilung von 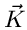 ist
ist
Wie man leicht zeigen kann, ist dieses die Laurent- Transformierte der
Multinominalverteilung oder verallgemeinerten Bernoulli- Verteilung
mit
Simulation der Multinominalverteilung
Ausgehend vom Wortmodell des vorigen Beispiels können wir ein einfaches
Simulationsprogramm für die Multinominalverteilung entwickeln.
Dazu führen wir das geschilderte Experiment auf unserem Rechner durch.
Wir generieren eine gleichverteilte Zufallszahl  aus dem Intervall
aus dem Intervall
![$(0,1]$](img281.gif) . Wir teilen das Intervall in
. Wir teilen das Intervall in 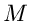 Teilintervalle
Teilintervalle
![$(x_{\mu-1},x_{\mu}]$](img282.gif) ein, und zwar so, daß
ein, und zwar so, daß
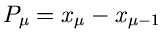 mit
mit 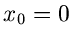 und
und 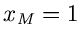 . Wir können dann im Einzelversuch die
Zuordnung
. Wir können dann im Einzelversuch die
Zuordnung
machen. Wir wiederholen den Versuch 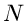 -mal und bilden den Vektor
-mal und bilden den Vektor
Die Komponenten dieses Vektors sollten dann gemäß einer
Multinominalverteilung verteilt sein.
Ein Java Applet zur Faltung von Verteilungen
Abschliessend möchten wir Sie noch animieren, sich das folgende
Applet,
anzuschauen.
In vielen Fällen ist die rechnerische Handhabung zur Bestimmung der Faltung zweier Verteilungen
ziemlich mühsam. Man behilft sich dann mit einer Simulation. Hierzu werden einfach zwei
Zufallszahlen mit den beiden Generatoren erzeugt und deren Summe gebildet.
Harm Fesefeldt
2006-05-08
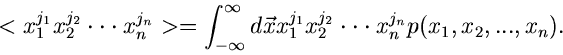
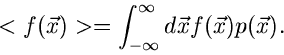
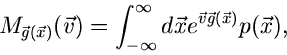
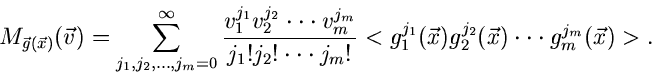
![]() :
:
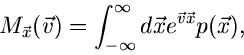
![]() :
:
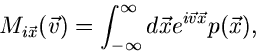
![]() :
:
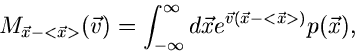
![]() :
:
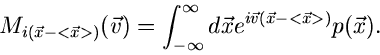
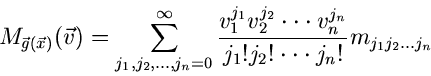
![]() :
:
![]() :
:
![]() :
:
![]() :
:
![]() statt mit
statt mit
![]() .
Aus den Reihenentwicklungen ersieht man insbesondere, daß für die
Laplace Transformierte
.
Aus den Reihenentwicklungen ersieht man insbesondere, daß für die
Laplace Transformierte
![]() gilt
gilt
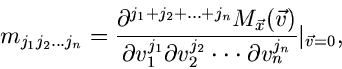

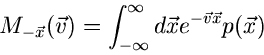
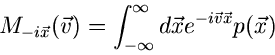
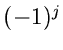 ergibt sich dasselbe wie bei den
erzeugenden und charakteristischen Funktionen.
ergibt sich dasselbe wie bei den
erzeugenden und charakteristischen Funktionen.
 mit der Wahrscheinlichkeitsverteilung
mit der Wahrscheinlichkeitsverteilung
![]() alle Formeln und Definitionen erhalten bleiben,
sofern man das Integralzeichen durch ein Summenzeichen ersetzt:
alle Formeln und Definitionen erhalten bleiben,
sofern man das Integralzeichen durch ein Summenzeichen ersetzt:

![]() ,
,
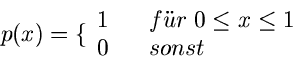
![\begin{displaymath}
M_{x}(v) = \int_{0}^{1} dx e^{vx} = \frac{1}{v} [e^{v}-1],
\end{displaymath}](img58.gif)
![\begin{displaymath}
M_{x-1/2}(v) = e^{-v/2} M_{x}(v) = \frac{1}{v} [e^{v/2} - e^{-v/2}] =
\frac{sinh(v/2)}{(v/2)}.
\end{displaymath}](img59.gif)

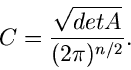

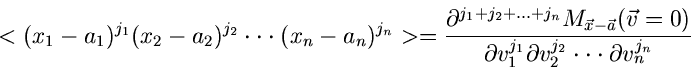

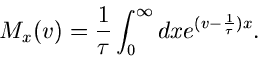
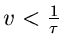 lösbar und ergibt
lösbar und ergibt
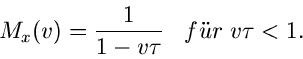
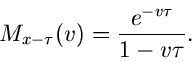
![]() -
Verteilung,
-
Verteilung,
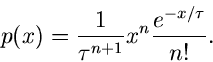
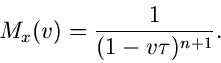
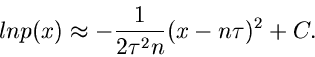
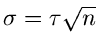 approximiert werden.
approximiert werden.
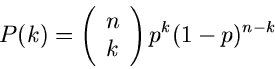
![\begin{displaymath}
M_{k}(v) = \sum_{k=0}^{\infty} e^{vk} P(k) = [1+(e^{v}-1)p]^{n}
\end{displaymath}](img90.gif)
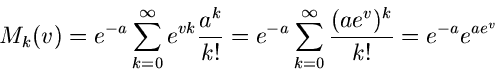
![]() -dimensionale Veränderliche
-dimensionale Veränderliche
![]() mit der Dichtefunktion
mit der Dichtefunktion
![]() . Seien alle
. Seien alle ![]() Veränderliche unabhängig
voneinander, d.h.
Veränderliche unabhängig
voneinander, d.h.

![]() durch
durch
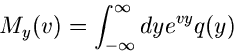
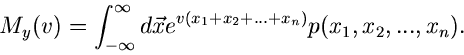
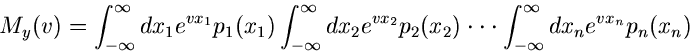
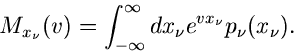
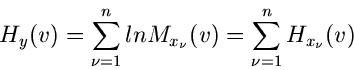


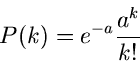
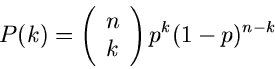

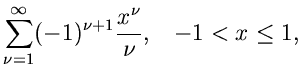
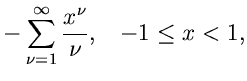
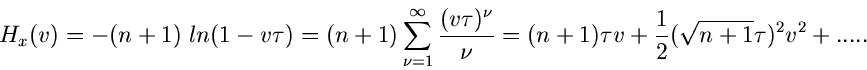
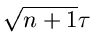 approximiert werden kann. Für
approximiert werden kann. Für ![]() die gleiche Dichtefunktion, d.h. wenn
die gleiche Dichtefunktion, d.h. wenn


![$\displaystyle n \; ln [1+(v m_{1} + \frac{1}{2} v^{2} m_{2})]$](img136.gif)
![$\displaystyle n \; [(v m_{1} + \frac{1}{2} v^{2} m_{2}) - \frac{1}{2} (v m_{1}
+ \frac{1}{2} v^{2} m_{2})^{2}]$](img137.gif)
![$\displaystyle n \; [v m_{1} + \frac{1}{2} v^{2} m_{2}
- \frac{1}{2} v^{2} m_{1}^{2} ]$](img138.gif)

![\begin{displaymath}
q(y) = \frac{1}{\sqrt{2 \pi n (m_{2}-m_{1}^{2})}}
e^{-(x-n m_{1})^{2}/[2n (m_{2}-m_{1}^{2})]}.
\end{displaymath}](img143.gif)
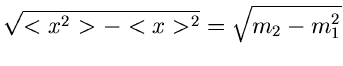
![\begin{displaymath}
q(y) = \frac{1}{\sqrt{2 \pi} \sigma_{y}} e^{-(y-<y>)^{2}/[2 \sigma_{y}^{2}]}.
\end{displaymath}](img152.gif)
![]() wirklich die Rücktransformierte der erzeugenden Funktion (31) ist.
Man kann diese Behauptung natürlich durch Einsetzen von
wirklich die Rücktransformierte der erzeugenden Funktion (31) ist.
Man kann diese Behauptung natürlich durch Einsetzen von ![]() in die
Definitionsgleichung (6) der erzeugenden Funktion und explizites
Lösen des Integrals zeigen. Auf ein allgemeines Verfahren zur
Rücktransformation werden wir später eingehen.
in die
Definitionsgleichung (6) der erzeugenden Funktion und explizites
Lösen des Integrals zeigen. Auf ein allgemeines Verfahren zur
Rücktransformation werden wir später eingehen.
![]() und
und ![]() zwei
unabhängige Veränderliche mit den Wahrscheinlichkeitsverteilungen
zwei
unabhängige Veränderliche mit den Wahrscheinlichkeitsverteilungen
![]() und
und ![]() . Mißt man beide Veränderliche
gleichzeitig, so ist wegen der Annahme der Unabhängigkeit die
zweidimensionale Verteilung durch
. Mißt man beide Veränderliche
gleichzeitig, so ist wegen der Annahme der Unabhängigkeit die
zweidimensionale Verteilung durch
![]() ist dann und nur dann null, wenn
ist dann und nur dann null, wenn ![]() und
und
![]() gleichzeitig null sind, daher
gleichzeitig null sind, daher
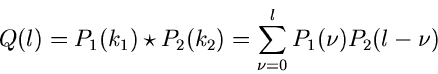
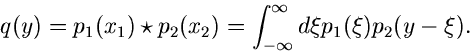
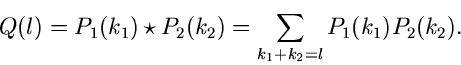

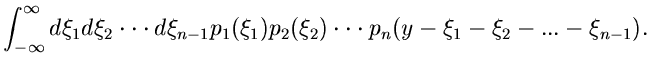
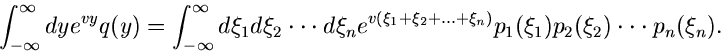
![]() mit der Dichtefunktion
mit der Dichtefunktion ![]() mit einem normalverteilten
Meßfehler
mit einem normalverteilten
Meßfehler ![]() ,
,
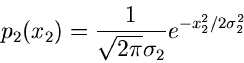

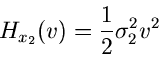

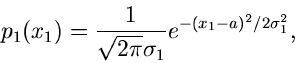
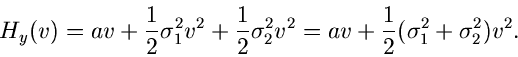
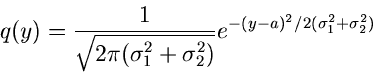
![]() anstatt der Normalverteilung
ist die Faltung im Prinzip ebenso einfach, jedoch hätten wir bei der
Rücktransformation von der erzeugenden Funktion zur Dichtefunktion einige
Probleme. Ein allgemeines Verfahren hierzu werden wir erst im nächsten Abschnitt
angeben.
anstatt der Normalverteilung
ist die Faltung im Prinzip ebenso einfach, jedoch hätten wir bei der
Rücktransformation von der erzeugenden Funktion zur Dichtefunktion einige
Probleme. Ein allgemeines Verfahren hierzu werden wir erst im nächsten Abschnitt
angeben.
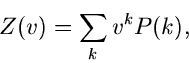
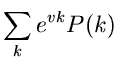
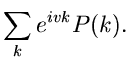
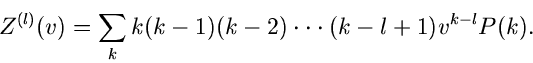
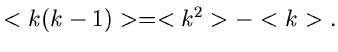
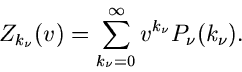
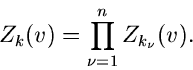
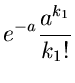
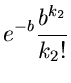

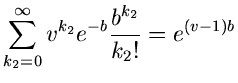
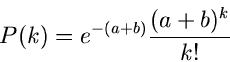
![]() und
und ![]() , besitzen.
, besitzen. ![]() und
und ![]() seien Elementarereignisse,
seien Elementarereignisse,
![]() als Ergebnis schließt das Ereignis
als Ergebnis schließt das Ereignis ![]() also aus und umgekehrt
schließt
also aus und umgekehrt
schließt ![]() das Ereignis
das Ereignis ![]() aus. Wir ordnen den Ereignissen
aus. Wir ordnen den Ereignissen
![]() und
und ![]() die zufälligen Veränderlichen
die zufälligen Veränderlichen ![]() und
und ![]() zu und definieren
zu und definieren
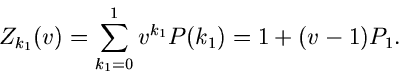
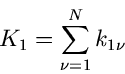
![\begin{displaymath}
Z_{K_{1}}(v) = \prod_{\nu=1}^{N} Z_{k_{1\nu}}(v) = [1+(v-1)P_{1}]^{N} .
\end{displaymath}](img249.gif)
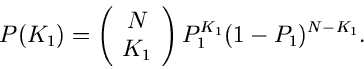
![\begin{displaymath}
Z_{K_{1}}(v) = \sum_{K_{1}=0}^{N} v^{K_{1}} \left( \begin{ar...
...right) P_{1}^{K_{1}} (1-P_{1})^{N-K_{1}} =
[1+(v-1)P_{1}]^{N}.
\end{displaymath}](img251.gif)

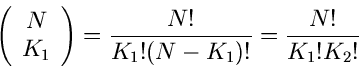
![]() zu
zu ![]() verschiedenen Elementarereignissen
verschiedenen Elementarereignissen
![]() führen kann. Wir definieren den diskreten Vektor
führen kann. Wir definieren den diskreten Vektor
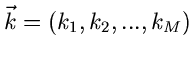 durch die Zuordnung
durch die Zuordnung
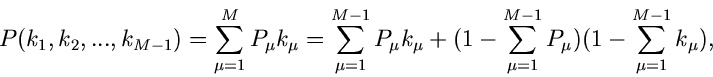
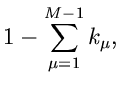
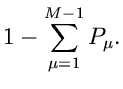
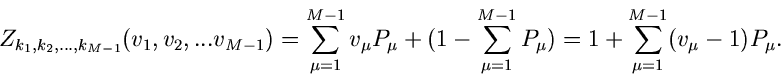
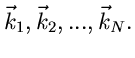 Die einzelnen Komponenten des Summenvektors
Die einzelnen Komponenten des Summenvektors
![\begin{displaymath}
Z_{K_{1},K_{2},...,K_{M-1}}(v_{1},v_{2},...,v_{M-1}) =
\prod...
...}(\vec{v}) =
[1+\sum_{\mu=1}^{M-1} (v_{\mu}-1) P_{\mu} ]^{N} .
\end{displaymath}](img276.gif)
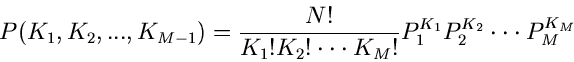
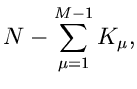
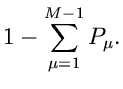
![]() aus dem Intervall
aus dem Intervall
![]() . Wir teilen das Intervall in
. Wir teilen das Intervall in ![]() Teilintervalle
Teilintervalle
![]() ein, und zwar so, daß
ein, und zwar so, daß
![]() mit
mit ![]() und
und ![]() . Wir können dann im Einzelversuch die
Zuordnung
. Wir können dann im Einzelversuch die
Zuordnung
![\begin{displaymath}
k_{\mu} = \{ \begin{array}{cl} 1 & \; \; \; wenn \; r\in (x_{\mu-1},x_{\mu}],
\\ 0 & \; \; \; sonst. \end{array}\end{displaymath}](img286.gif)