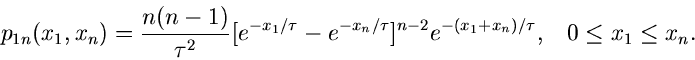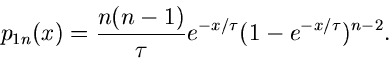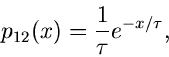Verteilungsfunktionen
Definitionen
Wir hatten im ersten Teil dieses Tutorials bereits die Zuordnung des Ereignisraumes auf zufällige
Veränderliche des reellen Zahlenraumes diskutiert. Hierbei wurde die
Wahrscheinlichkeitsdichte  dadurch definiert, daß
dadurch definiert, daß
 |
(1) |
die Wahrscheinlichkeit ist, daß die zufällige Veränderliche 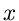 in das Intervall
in das Intervall
![$[\xi_{a},\xi_{b}]$](img7.gif) fällt. Für spätere Anwendungen definieren
wir noch zusätzlich die integrale Verteilungsfunktion, indem wir
fällt. Für spätere Anwendungen definieren
wir noch zusätzlich die integrale Verteilungsfunktion, indem wir
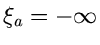 und
und 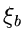 durch
durch 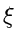 ersetzen:
ersetzen:
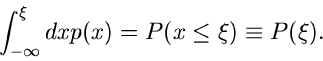 |
(2) |
Dieses gibt die Wahrscheinlichkeit an, daß die zufällige Veränderliche 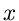 einen Wert kleiner als den festen Wert
einen Wert kleiner als den festen Wert 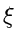 annimmt.
Diese Definition kann in einfacher
Weise auf zufällige Vektoren ausgedehnt werden.
annimmt.
Diese Definition kann in einfacher
Weise auf zufällige Vektoren ausgedehnt werden.
 |
(3) |
gibt dann die Wahrscheinlichkeit an, einen Wert des zufälligen Vektors
 zu finden mit
zu finden mit
 Offensichtlich ist
Offensichtlich ist
 |
(4) |
Daher gilt: Eine zufällige Veränderliche 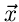 wird als gegeben
betrachtet, wenn eine dieser Funktionen,
wird als gegeben
betrachtet, wenn eine dieser Funktionen, 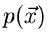 oder
oder 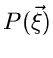 ,
gegeben ist.
,
gegeben ist.
Wir werden im folgenden die Wahrscheinlichkeitsdichte 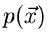 auch
häufig als Verteilungsfunktion und
auch
häufig als Verteilungsfunktion und 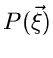 als integrale
Verteilungsfunktion bezeichnen. Diese Bezeichnungen sind in der Statistik
durchaus üblich. Streng genommen sollte man aber nur
als integrale
Verteilungsfunktion bezeichnen. Diese Bezeichnungen sind in der Statistik
durchaus üblich. Streng genommen sollte man aber nur 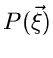 als Verteilungsfunktion bezeichnen.
als Verteilungsfunktion bezeichnen.
Für diskrete Veränderliche 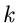 hatten wir keine Dichtefunktion definiert,
sondern nur die Wahrscheinlichkeitsverteilung. Die integrale
Verteilungsfunktion einer diskreten Veränderlichen wird definiert durch
hatten wir keine Dichtefunktion definiert,
sondern nur die Wahrscheinlichkeitsverteilung. Die integrale
Verteilungsfunktion einer diskreten Veränderlichen wird definiert durch
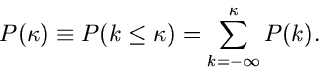 |
(5) |
Beispiele.
Es gibt nur wenige Wahrscheinlichkeitsverteilungen und Dichtefunktionen,
deren integrale Verteilungsfunktion geschlossen darstellbar ist. Nehmen wir
z.B. die Normalverteilung,
so ist die integrale Verteilungsfunktion
ein Integral, das nicht in geschlossener Form gelöst werden kann. Wir
hatten dieses Integral bereits im Zusammenhang mit dem
Fehlerintegral diskutiert. In Abbildung 1 zeigen wir einen Screenshot aus einem
Applet,
in dem die integrale Verteilungsfunktion mit Hilfe einer Simulation
numerisch bestimmt wird.
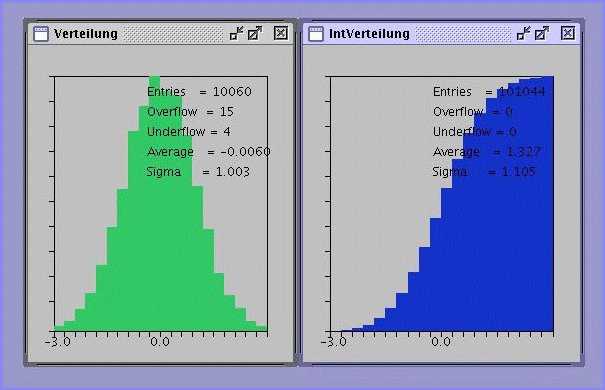
Abbildung 1:
Simulation der Normalverteilung und deren integrale
Verteilungsfunktion für
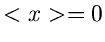 und
und 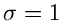 .
.
Ähnliches gilt für die Bernoulli Verteilung,
deren integrale Verteilungsfunktion
nicht mehr entscheidend in ihrer Form vereinfacht werden kann. Daher werden
wir die integrale Verteilungsfunktion nicht in den Vordergrund unserer
Betrachtungen stellen. In vielen Lehrbüchern der theoretischen Statistik
wird fast ausschließlich mit der integralen Verteilungsfunktion gearbeitet.
Der wesentliche Grund ist, daß dann in beiden Fällen, bei diskreten
und bei kontinuierlichen Veränderlichen, mit Wahrscheinlichkeiten
gearbeitet werden kann, die lästigen Fallunterscheidungen zwischen
diskreten und kontinuierlichen Veränderlichen damit entfallen.
Weiterhin sind die beiden Extremalbedingungen
theoretisch sehr nützlich.
Einige Beispiele von analytisch darstellbaren integralen Verteilungsfunktionen
sollen im folgenden noch angeführt werden.
Die Gleichverteilung im Intervall ![$[0,1]$](img27.gif) ,
,
hat offenbar die integrale Verteilungsfunktion
Die integrale Verteilungsfunktion der Exponentialverteilung
ist
und ist in Abb.2 gezeigt.
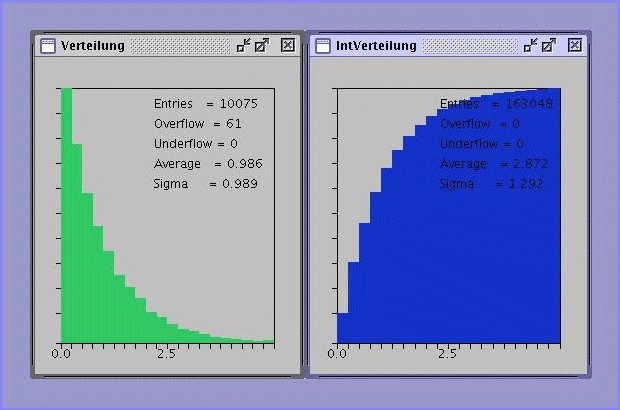
Abbildung 2:
Exponentialverteilung und integrale Exponentialverteilung für
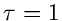 .
.
Randverteilungen
Wenn
 die integrale Verteilungsfunktion eines
zweidimensionalen zufälligen Vektors
die integrale Verteilungsfunktion eines
zweidimensionalen zufälligen Vektors
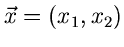 ist,
ist,
so kann man nach der Bedeutung der Funktion
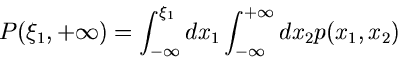 |
(6) |
fragen. Diese Funktion nennt man die integrale Randverteilung der zufälligen
Veränderlichen 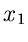 in der Verteilung von
in der Verteilung von 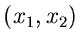 .
Da
.
Da
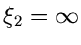 jetzt einen festen Wert annimmt, kann man auch schreiben
jetzt einen festen Wert annimmt, kann man auch schreiben
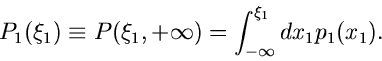 |
(7) |
Zur Randverteilung
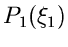 gehört also die Dichteverteilung
gehört also die Dichteverteilung
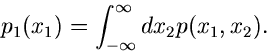 |
(8) |
Diese Definitionen lassen sich ohne weiteres auf  -dimensionale zufällige
Vektoren übertragen. So ist z.B. die Funktion
-dimensionale zufällige
Vektoren übertragen. So ist z.B. die Funktion
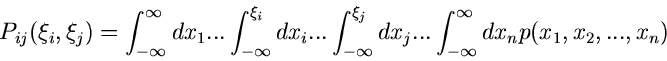 |
(9) |
die integrale Randverteilung der zweidimensionalen zufälligen
Veränderlichen 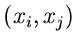 in der
in der  -dimensionalen zufälligen
Veränderlichen
-dimensionalen zufälligen
Veränderlichen
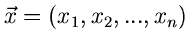 . Die zugehörige
Dichtefunktion ist entsprechend
. Die zugehörige
Dichtefunktion ist entsprechend
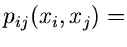 |
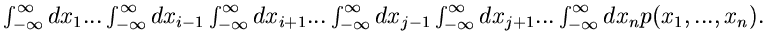 |
|
(10) |
Beispiel.
Die allgemeine zentrale Normalverteilung zweier Veränderlicher 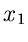 und
und
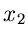 lautete:
lautete:
Zur Bestimmung der Randverteilungen integrieren wir über eine der beiden
Variablen. Wegen der Symmetrie ist es egal, über welche der beiden
Veränderlichen integriert wird.
Wir schreiben den Klammerausdruck im Exponenten des Integrals in der Form
und substituieren
Nach kurzer Rechnung erhalten wir
Die Dichtefunktion der Randverteilung einer zweidimensionalen Normalverteilung
ist also wieder eine Normalverteilung.
Reduktion von Variablen.
Eine besondere Art von Randverteilung hatten wir bereits im ersten Teil
kennengelernt, nämlich
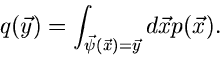 |
(11) |
Gemeint ist mit diesem Integral folgendes: Es soll eine
Variablentransformation
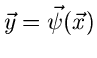 von der Veränderlichen
von der Veränderlichen
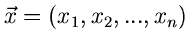 mit
mit  Komponenten zur Veränderlichen
Komponenten zur Veränderlichen
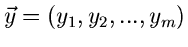 mit
mit 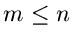 Komponenten durchgeführt
werden. Hierzu werden zunächst Hilfstransformationen
Komponenten durchgeführt
werden. Hierzu werden zunächst Hilfstransformationen
eingeführt und nach Ausführung der Transformation über diese
Hilfsvariablen
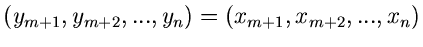 integriert.
integriert.
Bedingte Verteilungen
Die zweidimensionale zufällige Veränderliche 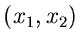 sei durch die
Dichtefunktion
sei durch die
Dichtefunktion
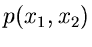 oder durch die integrale Verteilungsfunktion
oder durch die integrale Verteilungsfunktion
 gegeben. Wir fragen jetzt nach der Wahrscheinlichkeit,
daß die Veränderliche
gegeben. Wir fragen jetzt nach der Wahrscheinlichkeit,
daß die Veränderliche 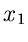 in das Intervall
in das Intervall
![$[-\infty,\xi_{1}]$](img68.gif) und
die Veränderliche
und
die Veränderliche 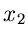 in das Intervall
in das Intervall
![$[\xi_{2},\xi_{2}+h]$](img69.gif) fällt.
Diese Wahrscheinlichkeit ist offenbar
fällt.
Diese Wahrscheinlichkeit ist offenbar
Dividiert man beide Seiten durch
so erhält man die Wahrscheinlichkeit dafür, daß
 ist,
aber nun unter der Voraussetzung, daß
ist,
aber nun unter der Voraussetzung, daß 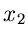 in das Intervall
in das Intervall
![$[\xi_{2},\xi_{2}+h]$](img69.gif) fällt. Man nennt dieses die bedingte Wahrscheinlichkeit
und schreibt dafür
fällt. Man nennt dieses die bedingte Wahrscheinlichkeit
und schreibt dafür
Die letzte Formel kann offenbar auch geschrieben werden als
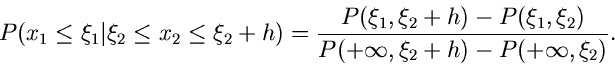 |
(12) |
Dieses ist eine eindimensionale Verteilung mit der Normierung
Um die Dichtefunktion dieser Verteilung zu erhalten, dividieren wir Zähler
und Nenner der rechten Seite von (12) durch 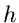 und erhalten im
Grenzübergang
und erhalten im
Grenzübergang 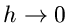 :
:
Da
erhält man
und daher
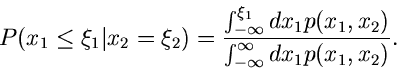 |
(13) |
Man nennt
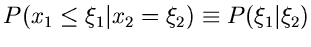 die bedingte Wahrscheinlichkeit dafür, daß
die bedingte Wahrscheinlichkeit dafür, daß
 , unter der
Voraussetzung, daß
, unter der
Voraussetzung, daß
 . Die zugehörige Dichtefunktion
kann man aus der vorigen Formel sofort ablesen:
. Die zugehörige Dichtefunktion
kann man aus der vorigen Formel sofort ablesen:
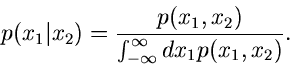 |
(14) |
Mit dieser Schreibweise ist dann auch
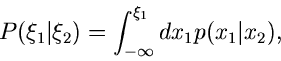 |
(15) |
wie es für eine eindimensionale Verteilung sein muß.
Der Begriff der bedingten Dichtefunktion kann leicht auf mehrere
Veränderliche übertragen werden. Gegeben sei eine  -dimensionale
Veränderliche
-dimensionale
Veränderliche
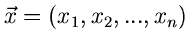 . Dann ist
. Dann ist
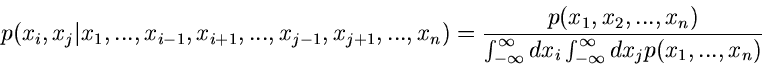 |
(16) |
die Dichtefunktion der Veränderlichen 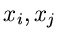 unter der
Voraussetzung, daß die übrigen
unter der
Voraussetzung, daß die übrigen 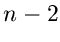 Veränderlichen die festen Werte
Veränderlichen die festen Werte
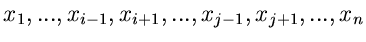 annehmen.
annehmen.
Beispiel.
Wir greifen wiederum die zweidimensionale zentrale Normalverteilung
auf und fragen nach der Dichtefunktion für 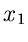 bei vorgegebenem,
festgehaltenem
bei vorgegebenem,
festgehaltenem 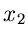 ,
,
Wegen
folgt nach einfacher Umformung des Exponenten
Dieses ist eine Normalverteilung mit Erwartungswert
und Varianz
Unabhängige Veränderliche
Wir hatten zwei Veränderliche unabhängig voneinander genannt, wenn sich
ihre Dichtefunktion faktorisieren läßt:
Unter dieser Voraussetzung ist aber
und damit auch
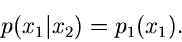 |
(17) |
Die bedingte Wahrscheinlichkeit der Veränderlichen 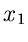 für
festgehaltenes
für
festgehaltenes 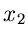 hängt in diesem Fall überhaupt nicht von
hängt in diesem Fall überhaupt nicht von 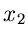 ab. Für eine Dichtefunktion mehrerer Veränderlicher, die alle unabhängig
voneinander sind,
ab. Für eine Dichtefunktion mehrerer Veränderlicher, die alle unabhängig
voneinander sind,
folgt entsprechend
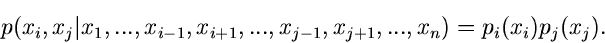 |
(18) |
Beispiel.
In unserem schon hinreichen bekannten Beispiel der zweidimensionalen
Normalverteilung
sind 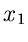 und
und 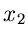 nicht unabhängig, solange der Korrelationskoeffizient
nicht unabhängig, solange der Korrelationskoeffizient
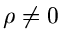 ist. Für
ist. Für 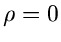 läßt sich die Verteilung faktorisieren in
läßt sich die Verteilung faktorisieren in
 und
und  sind unter diesen Voraussetzungen unabhängig.
sind unter diesen Voraussetzungen unabhängig.
Für 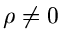 können wir eine faktorisierte Dichtefunktion erreichen,
indem wir vorher eine Transformation der Variablen durchgeführt haben.
Dieses Verfahren wurde bereits in aller Länge im ersten Teil dieses Tutorials durchgerechnet.
Wir wiederholen das Ergebnis. Die Transformation
können wir eine faktorisierte Dichtefunktion erreichen,
indem wir vorher eine Transformation der Variablen durchgeführt haben.
Dieses Verfahren wurde bereits in aller Länge im ersten Teil dieses Tutorials durchgerechnet.
Wir wiederholen das Ergebnis. Die Transformation
führt auf die Dichtefunktion
die sich leicht fakrorisieren läßt. 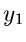 und
und 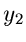 sind unabhängig
voneinander,
sind unabhängig
voneinander, 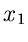 und
und 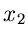 dagegen nicht. Diese Technik der
Faktorisierung von abhängigen Veränderlichen nach Einführung einer
geeigneten Transformation wird uns bei Aufgaben der Simulation nach
häufiger beschäftigen.
dagegen nicht. Diese Technik der
Faktorisierung von abhängigen Veränderlichen nach Einführung einer
geeigneten Transformation wird uns bei Aufgaben der Simulation nach
häufiger beschäftigen.
Geordnete Statistik
In späteren Kapiteln werden wir wichtige Aussagen aus der Theorie der
geordneten Statistik benötigen. Angenommen, wir messen eine zufällige
Veränderliche mit der Dichtefunktion 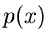 und der integralen
Verteilungsfunktion
und der integralen
Verteilungsfunktion
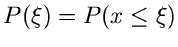 . Bei
. Bei  unabhängigen
Messungen erhalten wir die Ergebnisse
unabhängigen
Messungen erhalten wir die Ergebnisse
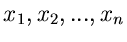 mit der
Dichtefunktion
mit der
Dichtefunktion
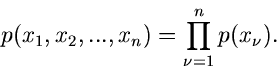 |
(19) |
Wir ordnen jetzt die Messungen der Größe nach in aufsteigender
Reihenfolge und bezeichnen die so erhaltenen Ergebnisse mit
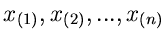 . Dann gilt also:
. Dann gilt also:
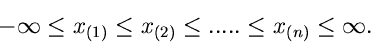 |
(20) |
Das Problem der geordneten Statistik ist das Auffinden der Dichtefunktion
 .
.
Die eindimensionalen Randverteilungen.
Zur Einführung in das angeschnittene allgemeine Problem stellen wir
zunächst zwei einfache Fragen, nämlich die Verteilungen
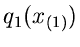 und
und
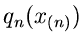 des kleinsten und des größten Wertes
des kleinsten und des größten Wertes 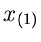 und
und
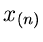 .
.
Die Wahrscheinlichkeit dafür, daß
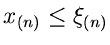 , ist
gleichbedeutend mit der Wahrscheinlichkeit, daß alle
, ist
gleichbedeutend mit der Wahrscheinlichkeit, daß alle
 . In Formeln besagt diese Aussage, daß für die
integrale Verteilungsfunktion
. In Formeln besagt diese Aussage, daß für die
integrale Verteilungsfunktion
gilt:
Daraus erhalten wir sofort die Dichtefunktion für den größten Wert zu
![\begin{displaymath}
q_{n}(x_{(n)}) = \left( \frac{dQ_{n}(\xi_{(n)})}{d\xi_{(n)}}...
...}} =
n [ P(\xi_{(n)})]_{\xi_{(n)}=x_{(n)}}^{n-1} p(x_{(n)}).
\end{displaymath}](img129.gif) |
(21) |
Man erhält also ein Produkt aus der differentiellen und integralen Verteilungsfunktion.
Aus ähnlichen Überlegungen erhält man für die Dichtefunktion des kleinsten
Wertes 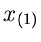 :
:
![\begin{displaymath}
q_{1}(x_{(1)}) = n [1-P(\xi_{(1)})]_{\xi_{(1)}=x_{(1)}}^{n-1} p(x_{(1)}).
\end{displaymath}](img130.gif) |
(22) |
Allgemeiner ist die Wahrscheinlichkeit, daß für irgendein Index 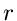 mit
mit
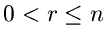 das Ereignis
das Ereignis
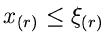 eintritt, gleichbedeutend
mit der Wahrscheinlichkeit, daß exakt
eintritt, gleichbedeutend
mit der Wahrscheinlichkeit, daß exakt 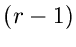 der Zahlen
der Zahlen
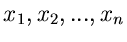 kleiner als
kleiner als 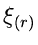 sein müssen, und umgekehrt
sein müssen, und umgekehrt 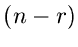 der Zahlen größer
als
der Zahlen größer
als 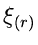 sein müssen. Offensichtlich muß die Dichtefunktion durch
ein Produkt aus Faktoren ähnlich denen in Formel (21) und (22)
darstellbar sein. Ohne Beweis schreiben wir das Endergebnis an:
sein müssen. Offensichtlich muß die Dichtefunktion durch
ein Produkt aus Faktoren ähnlich denen in Formel (21) und (22)
darstellbar sein. Ohne Beweis schreiben wir das Endergebnis an:
![\begin{displaymath}
q_{r}(x_{(r)}) = \frac{n!}{(r-1)! (n-r)!}
[P(\xi_{(r)})]_{\...
...r-1}
[1 - P(\xi_{(r)})]_{\xi_{(r)}=x_{(r)}}^{n-r} p(x_{(r)}).
\end{displaymath}](img137.gif) |
(23) |
Der Normierungsfaktor drückt die Tatsache aus, daß es nicht auf die
Reihenfolge der 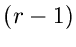 kleinsten bzw
kleinsten bzw 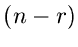 größten Zahlen untereinander
ankommt. Man prüft leicht nach, daß (21) und (22) als Spezialfälle
in Formel (23) enthalten sind.
größten Zahlen untereinander
ankommt. Man prüft leicht nach, daß (21) und (22) als Spezialfälle
in Formel (23) enthalten sind.
Mehrdimensionale Randverteilungen.
In völlig analoger Weise kann man die Dichtefunktion zweier Veränderlicher
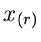 und
und 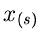 aus einer geordneten Zahlenfolge von
aus einer geordneten Zahlenfolge von  Veränderlichen
Veränderlichen
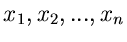 herleiten. Das Ergebnis ist:
herleiten. Das Ergebnis ist:
Die Verallgemeinerung auf 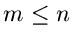 Veränderliche liegt auf der Hand
und lautet:
Veränderliche liegt auf der Hand
und lautet:
Diese etwas komplizierte Formel kann man für viele Fälle stark vereinfachen.
Für 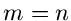 erhält man insbesondere die einfache Formel
erhält man insbesondere die einfache Formel
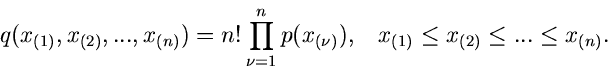 |
(25) |
Man beachte die einschränkende Nebenbedingung für den Gültigkeitsbereich
der Veränderlichen. Daher sind die 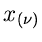 , im Gegensatz zu den
, im Gegensatz zu den
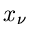 , auch nicht mehr unabhängig voneinander, obwohl man dieses
fälschlicherweise aus der Form der Dichtefunktion schließen könnte.
, auch nicht mehr unabhängig voneinander, obwohl man dieses
fälschlicherweise aus der Form der Dichtefunktion schließen könnte.
Beispiel.
Zur Illustration rechnen wir den für unsere späteren Erörterungen
wichtigsten Fall explizit durch. Wir erzeugen  Zufallszahlen
Zufallszahlen
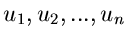 aus der Gleichverteilung im Intervall
aus der Gleichverteilung im Intervall ![$[0,1]$](img27.gif) .
Die geordnete Reihe bezeichnen wir mit
.
Die geordnete Reihe bezeichnen wir mit
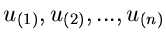 .
Die Dichtefunktion der ursprünglichen Zufallszahlen ist
.
Die Dichtefunktion der ursprünglichen Zufallszahlen ist
mit der integralen Verteilungsfunktion
Die Dichtefunktion der 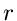 -ten geordneten Zufallszahl aus einer Reihe von
-ten geordneten Zufallszahl aus einer Reihe von
 Zufallszahlen ergibt sich damit zu
Zufallszahlen ergibt sich damit zu
Insbesondere ist die Dichtefunktion des kleinsten und größten Wertes:
Die zweidimensionale Dichtefunktion in 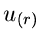 und
und 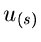 kann man
ebenfalls sofort hinschreiben.
kann man
ebenfalls sofort hinschreiben.
Wir benützen dieses Ergebnis, um die Dichtefunktion der Differenz
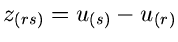 zu bestimmen. Dazu führen wir die naheliegende
Transformation
zu bestimmen. Dazu führen wir die naheliegende
Transformation
ein. Ausführung der Transformation liefert
Die Randverteilung in 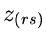 ist:
ist:
Führt man noch 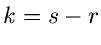 und
und
 ein,
so erhält man die einfache Formel
ein,
so erhält man die einfache Formel
Diese Dichtefunktion hängt offenbar nicht von den speziellen Werten von
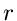 und
und  , sondern nur von der Differenz
, sondern nur von der Differenz 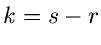 ab. Für spätere
Anwendungen bemerken wir noch, daß die Dichtefunktion
ab. Für spätere
Anwendungen bemerken wir noch, daß die Dichtefunktion  ein
Spezialfall der allgemeinen Betaverteilung
ein
Spezialfall der allgemeinen Betaverteilung
mit 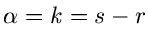 und
und
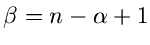 ist.
ist.
Wir haben dieses Beispiel in einem
Applet
programmiert. In einem Versuch werden
jeweils 10 Zufallszahlen generiert und der Grösse nach sortiert. In einem Auswahlmenue
kann der Benutzer Plots auswählen.
Beispiel.
Ein zweites interessantes Beispiel im Zusammenhang mit der geordneten
Statistik ist der radioaktive Zerfall. Wir denken uns eine Quelle mit
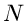 radioaktiven Kernen. Die Zahl
radioaktiven Kernen. Die Zahl 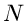 liegt in praktischen Anwendungen immer
in der Größenordnung der Avogadroschen Zahl (
liegt in praktischen Anwendungen immer
in der Größenordnung der Avogadroschen Zahl (
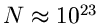 ). Wir
nehmen an, daß der Zerfall eines Kernes nicht von den anderen Kernen
beeinflußt wird, die Zerfälle verschiedener Kerne also unabhängig
voneinander ablaufen. Die Zerfallswahrscheinlichkeit eines Kernes als
Funktion der Zeit wird durch die Dichtefunktion
). Wir
nehmen an, daß der Zerfall eines Kernes nicht von den anderen Kernen
beeinflußt wird, die Zerfälle verschiedener Kerne also unabhängig
voneinander ablaufen. Die Zerfallswahrscheinlichkeit eines Kernes als
Funktion der Zeit wird durch die Dichtefunktion
beschrieben. Die integrale Verteilungsfunktion ist:
In diesem Beispiel liefert uns die Natur bereits eine geordnete Statistik,
d.h.
 . Daher ist die
Dichtefunktion des Vektors
. Daher ist die
Dichtefunktion des Vektors
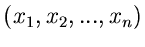 durch
durch
gegeben. Insbesondere ergibt sich für die zweidimensionale Verteilung
Besonders interessant im Hinblick auf Messungen ist hierbei die Verteilung
der Zeitdiffenez 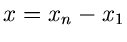 zwischen der ersten und der
zwischen der ersten und der  -ten
Zählermessung. Der Versuch sieht folgendermaßen aus: Ein Zähler
und ein TDC (time digital converter) werden durch einen beliebigen Zerfall
gestartet. Bei jedem weiteren Zerfall wird der Zähler um eins hochgesetzt.
Bei der Zählrate
-ten
Zählermessung. Der Versuch sieht folgendermaßen aus: Ein Zähler
und ein TDC (time digital converter) werden durch einen beliebigen Zerfall
gestartet. Bei jedem weiteren Zerfall wird der Zähler um eins hochgesetzt.
Bei der Zählrate  wird der TDC gestoppt und die Zeitdifferenz gemessen.
Aus der obigen Formel folgt für diesen speziellen Fall:
wird der TDC gestoppt und die Zeitdifferenz gemessen.
Aus der obigen Formel folgt für diesen speziellen Fall:
Die Transformation
führt nach Integration über  auf die Randverteilung
auf die Randverteilung
Dieses ist eine wichtige Formel zur Messung der Lebensdauer 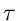 .
Die Verteilung der Zeitdifferenz zwischen aufeinanderfolgenden Zerfällen
(
.
Die Verteilung der Zeitdifferenz zwischen aufeinanderfolgenden Zerfällen
(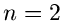 ) ist insbesondere
) ist insbesondere
also identisch mit der ursprünglichen Dichtefunktion des radioaktiven
Zerfalls. Die wesentliche Aussage ist: Die Zerfallswahrscheinlichkeit
eines radioaktiven Kernes hängt nicht vom Zeitnullpunkt ab.
In manchen Lehrbüchern der Statistik wird die letztere Aussage als Postulat
eingeführt und daraus das Zerfallsgesetz des radioaktiven Zerfalls hergeleitet.
Harm Fesefeldt
2006-05-05


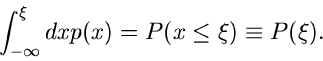


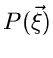 ,
gegeben ist.
,
gegeben ist.
![]() auch
häufig als Verteilungsfunktion und
auch
häufig als Verteilungsfunktion und 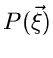 als integrale
Verteilungsfunktion bezeichnen. Diese Bezeichnungen sind in der Statistik
durchaus üblich. Streng genommen sollte man aber nur
als integrale
Verteilungsfunktion bezeichnen. Diese Bezeichnungen sind in der Statistik
durchaus üblich. Streng genommen sollte man aber nur 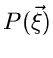 als Verteilungsfunktion bezeichnen.
als Verteilungsfunktion bezeichnen.
![]() hatten wir keine Dichtefunktion definiert,
sondern nur die Wahrscheinlichkeitsverteilung. Die integrale
Verteilungsfunktion einer diskreten Veränderlichen wird definiert durch
hatten wir keine Dichtefunktion definiert,
sondern nur die Wahrscheinlichkeitsverteilung. Die integrale
Verteilungsfunktion einer diskreten Veränderlichen wird definiert durch
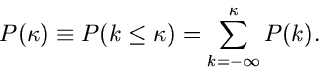
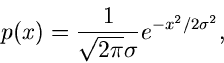
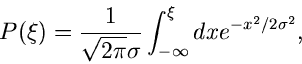

![]() und
und ![]() .
.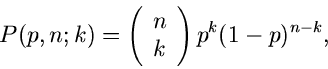

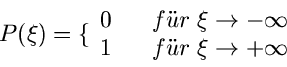
![]() ,
,
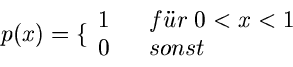
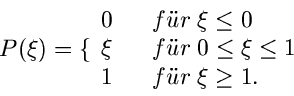
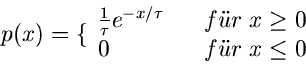
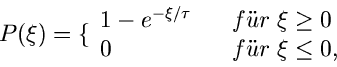

![]() .
.![]() die integrale Verteilungsfunktion eines
zweidimensionalen zufälligen Vektors
die integrale Verteilungsfunktion eines
zweidimensionalen zufälligen Vektors
![]() ist,
ist,

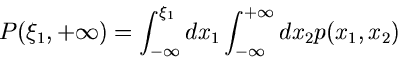
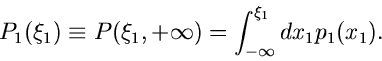
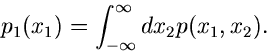
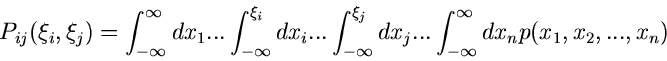
![]() und
und
![]() lautete:
lautete:

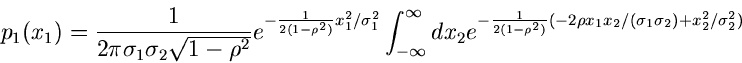
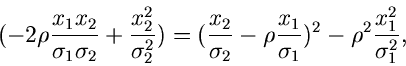
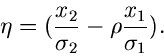

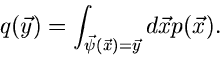
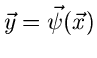 von der Veränderlichen
von der Veränderlichen
![]() sei durch die
Dichtefunktion
sei durch die
Dichtefunktion
![]() oder durch die integrale Verteilungsfunktion
oder durch die integrale Verteilungsfunktion
![]() gegeben. Wir fragen jetzt nach der Wahrscheinlichkeit,
daß die Veränderliche
gegeben. Wir fragen jetzt nach der Wahrscheinlichkeit,
daß die Veränderliche ![]() in das Intervall
in das Intervall
![]() und
die Veränderliche
und
die Veränderliche ![]() in das Intervall
in das Intervall
![]() fällt.
Diese Wahrscheinlichkeit ist offenbar
fällt.
Diese Wahrscheinlichkeit ist offenbar
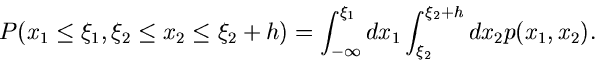
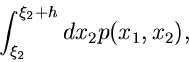
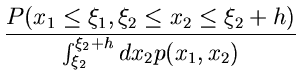

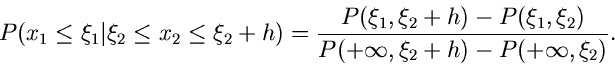
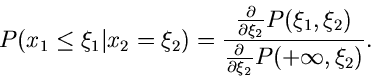
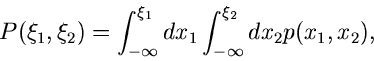
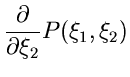
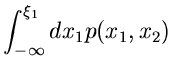
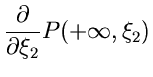
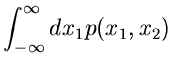
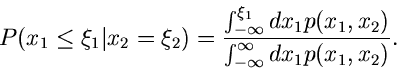
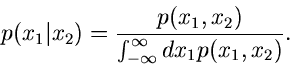
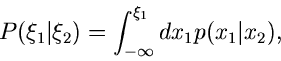
![]() -dimensionale
Veränderliche
-dimensionale
Veränderliche
![]() . Dann ist
. Dann ist
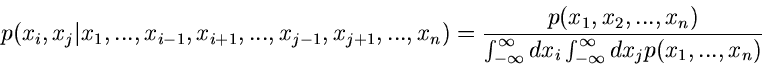
![]() bei vorgegebenem,
festgehaltenem
bei vorgegebenem,
festgehaltenem ![]() ,
,
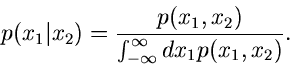

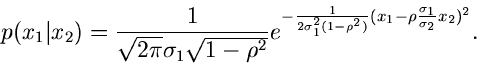
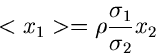
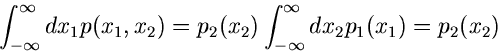
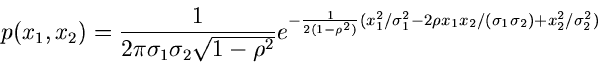
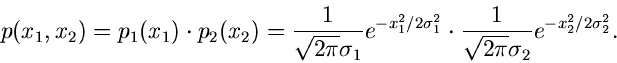
![]() können wir eine faktorisierte Dichtefunktion erreichen,
indem wir vorher eine Transformation der Variablen durchgeführt haben.
Dieses Verfahren wurde bereits in aller Länge im ersten Teil dieses Tutorials durchgerechnet.
Wir wiederholen das Ergebnis. Die Transformation
können wir eine faktorisierte Dichtefunktion erreichen,
indem wir vorher eine Transformation der Variablen durchgeführt haben.
Dieses Verfahren wurde bereits in aller Länge im ersten Teil dieses Tutorials durchgerechnet.
Wir wiederholen das Ergebnis. Die Transformation


![]() und der integralen
Verteilungsfunktion
und der integralen
Verteilungsfunktion
![]() . Bei
. Bei ![]() unabhängigen
Messungen erhalten wir die Ergebnisse
unabhängigen
Messungen erhalten wir die Ergebnisse
![]() mit der
Dichtefunktion
mit der
Dichtefunktion
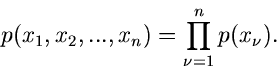
![]() und
und
![]() des kleinsten und des größten Wertes
des kleinsten und des größten Wertes ![]() und
und
![]() .
.
![]() , ist
gleichbedeutend mit der Wahrscheinlichkeit, daß alle
, ist
gleichbedeutend mit der Wahrscheinlichkeit, daß alle
![]() . In Formeln besagt diese Aussage, daß für die
integrale Verteilungsfunktion
. In Formeln besagt diese Aussage, daß für die
integrale Verteilungsfunktion
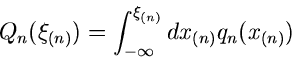
![\begin{displaymath}
q_{n}(x_{(n)}) = \left( \frac{dQ_{n}(\xi_{(n)})}{d\xi_{(n)}}...
...}} =
n [ P(\xi_{(n)})]_{\xi_{(n)}=x_{(n)}}^{n-1} p(x_{(n)}).
\end{displaymath}](img129.gif)
![\begin{displaymath}
q_{r}(x_{(r)}) = \frac{n!}{(r-1)! (n-r)!}
[P(\xi_{(r)})]_{\...
...r-1}
[1 - P(\xi_{(r)})]_{\xi_{(r)}=x_{(r)}}^{n-r} p(x_{(r)}).
\end{displaymath}](img137.gif)
![]() und
und ![]() aus einer geordneten Zahlenfolge von
aus einer geordneten Zahlenfolge von ![]() Veränderlichen
Veränderlichen
![]() herleiten. Das Ergebnis ist:
herleiten. Das Ergebnis ist:
![$\displaystyle \frac{n!}{(r-1)! (s-r-1)! (n-s)!}
[P(\xi_{(r)})]_{\xi_{(r)}=x_{(r...
...{r-1}
[P(\xi_{(s)})-P(\xi_{(r)})]_{\xi_{(s)}=x_{(s)},\xi_{(r)}=x_{(r)}}^{s-r-1}$](img141.gif)
![$\displaystyle [1-P(\xi_{(s)})]_{\xi_{(s)}=x_{(s)}}^{n-s} p(x_{(r)}) p(x_{(s)}), \; \; \;
x_{(r)} \leq x_{(s)}.$](img143.gif)
![$\displaystyle n! \frac{[P(\xi_{(r_{1})})]_{\xi_{(r_{1})}=x_{(r_{1})}}^{r_{1}-1}}{(r_{1}-1)!}$](img145.gif)
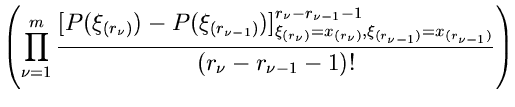
![$\displaystyle \frac{[1-P(\xi_{(r_{m})})]_{\xi_{(r_{m})}=x_{(r_{m})}}^{n-r_{m}}}
{(n-r_{m})!} \prod_{\nu=1}^{m} p(x_{(r_{\nu})}),$](img147.gif)
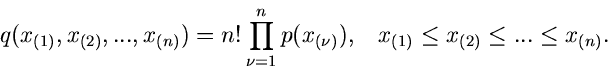
![]() Zufallszahlen
Zufallszahlen
![]() aus der Gleichverteilung im Intervall
aus der Gleichverteilung im Intervall ![]() .
Die geordnete Reihe bezeichnen wir mit
.
Die geordnete Reihe bezeichnen wir mit
![]() .
Die Dichtefunktion der ursprünglichen Zufallszahlen ist
.
Die Dichtefunktion der ursprünglichen Zufallszahlen ist
![\begin{displaymath}[P(\xi_{\nu})]_{\xi_{\nu}=u_{\nu}} = \{ \begin{array}{lll}
0 ...
...leq u_{\nu} \leq 1, \\
1 & f''ur & 1 \leq u_{\nu}. \end{array}\end{displaymath}](img157.gif)

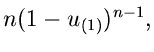
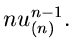
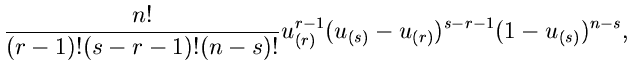

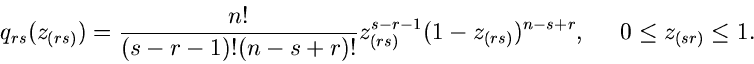
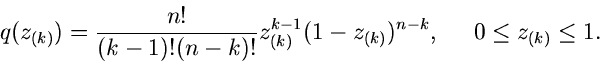

![]() radioaktiven Kernen. Die Zahl
radioaktiven Kernen. Die Zahl ![]() liegt in praktischen Anwendungen immer
in der Größenordnung der Avogadroschen Zahl (
liegt in praktischen Anwendungen immer
in der Größenordnung der Avogadroschen Zahl (
![]() ). Wir
nehmen an, daß der Zerfall eines Kernes nicht von den anderen Kernen
beeinflußt wird, die Zerfälle verschiedener Kerne also unabhängig
voneinander ablaufen. Die Zerfallswahrscheinlichkeit eines Kernes als
Funktion der Zeit wird durch die Dichtefunktion
). Wir
nehmen an, daß der Zerfall eines Kernes nicht von den anderen Kernen
beeinflußt wird, die Zerfälle verschiedener Kerne also unabhängig
voneinander ablaufen. Die Zerfallswahrscheinlichkeit eines Kernes als
Funktion der Zeit wird durch die Dichtefunktion
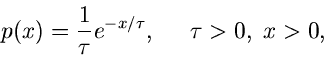
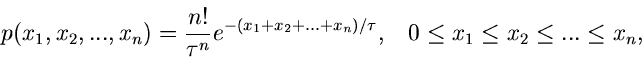
![$\displaystyle \frac{n!}{(r-1)! (s-r-1)! (n-s)!}
[1-e^{x_{r}/\tau}]^{r-1} [e^{-x_{r}/\tau} - e^{-x_{s}/\tau}]^{s-r-1}$](img194.gif)
![$\displaystyle [e^{-x_{s}/\tau}]^{n-s} \frac{1}{\tau^{2}} e^{-(x_{r}+x_{s})/\tau},$](img195.gif)