Laplace- und Fourier- Transformation
Klassifizierung
Durch eine Funktion 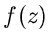 hatten wir jeder Zahl
hatten wir jeder Zahl 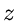 eine neue Zahl
eine neue Zahl 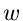 zugeordnet, nämlich
zugeordnet, nämlich 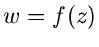 . Dieses kann man verallgemeinern zum Begriff
der Funktionaltransformation. Gegeben sei eine bestimmte Menge von
Funktionen, z.B. die Menge der stetigen Funktionen oder die Menge der
trigonometrischen Funktionen. Bei einer Funktionaltransformation wird nun
jeder Funktion
. Dieses kann man verallgemeinern zum Begriff
der Funktionaltransformation. Gegeben sei eine bestimmte Menge von
Funktionen, z.B. die Menge der stetigen Funktionen oder die Menge der
trigonometrischen Funktionen. Bei einer Funktionaltransformation wird nun
jeder Funktion 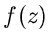 aus der Originalmenge eine Funktion
aus der Originalmenge eine Funktion 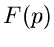 aus der
Bildmenge zugeordnet. Die wichtigsten Transformationen sind die
Integraltransformationen
aus der
Bildmenge zugeordnet. Die wichtigsten Transformationen sind die
Integraltransformationen
 |
(1) |
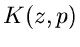 nennt man den Kern der Transformation. Häufig benutzte
Transformationen sind
nennt man den Kern der Transformation. Häufig benutzte
Transformationen sind
Eine weitere Klassifikation kann noch durch die Wahl der Integrationsgrenzen
vorgenommen werden.
Aus der Integraldefinition kann man eine weitere Klasse von Transformationen
herleiten, nämlich die diskreten Transformationen. Ein Beispiel ist
Wichtig ist hierbei, daß die Funktion 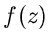 nur an den diskreten Punkten
nur an den diskreten Punkten
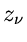 bekannt oder gemessen zu sein braucht. Hat die Zahlenfolge
bekannt oder gemessen zu sein braucht. Hat die Zahlenfolge
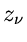 die equidistanten Werte
die equidistanten Werte
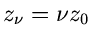 , so kann man den
dann für alle
, so kann man den
dann für alle 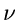 konstanten Faktor
konstanten Faktor
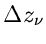 weglassen und
erhält
weglassen und
erhält
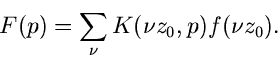 |
(2) |
Eine der wichtigsten Transformationen dieser Art hat den Kern
und heißt 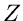 - Transformation (
- Transformation ( bis
bis  ) oder Laurent-
Transformation (
) oder Laurent-
Transformation (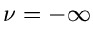 bis
bis  ). Es sind dieses besonders
die Laplace- Transformation, die Fourier- Transformation und diese beiden
letzteren diskreten Transformationen, mit denen wir uns im folgenden
beschäftigen werden.
). Es sind dieses besonders
die Laplace- Transformation, die Fourier- Transformation und diese beiden
letzteren diskreten Transformationen, mit denen wir uns im folgenden
beschäftigen werden.
Wir schreiben die Laplace- Transformation im folgenden in der Form
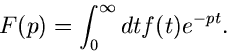 |
(3) |
Hierbei ist also, wie oben schon erwähnt, 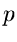 eine komplexe Zahl, die wir
immer mit
eine komplexe Zahl, die wir
immer mit
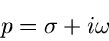 |
(4) |
in Real- und Imaginärteil zerlegen werden, und 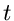 eine reelle Zahl,
die im allgemeinen, aber nicht immer, die Bedeutung der Zeit hat.
Man spricht von der einseitigen Laplace- Transformation, wenn, wie in
Formel (3), die untere Integrationsgrenze gleich 0 gesetzt wird,
dagegen von der zweiseitigen Laplace- Transformation, wenn
eine reelle Zahl,
die im allgemeinen, aber nicht immer, die Bedeutung der Zeit hat.
Man spricht von der einseitigen Laplace- Transformation, wenn, wie in
Formel (3), die untere Integrationsgrenze gleich 0 gesetzt wird,
dagegen von der zweiseitigen Laplace- Transformation, wenn
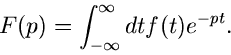 |
(5) |
In diesem Kapitel werden wir uns ausschließlich mit der einseitigen
Laplace- Transformation beschäftigen. In späteren Kapiteln werden wir
aber auch die zweiseitige Laplace- Transformation benötigen. Die
entsprechenden Formeln müssen dann teilweise geringfügig geändert
werden.
Statt der Integralformel schreibt man zur Abkürzung
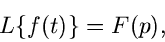 |
(6) |
was heißen soll, daß die Laplace- Transformierte der Funktion 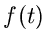 die Funktion
die Funktion 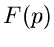 ist. Oder anders ausgedrückt, durch Anwendung
der Operation
ist. Oder anders ausgedrückt, durch Anwendung
der Operation
geht die Funktion 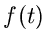 über in
über in 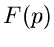 :
:
Wir bezeichnen immer die Originalfunktion mit kleinen und die Bildfunktion
mit großen Buchstaben. Die inverse Transformation drückt man durch die
Bezeichnung
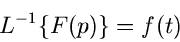 |
(7) |
aus. Dieses bedeutet, daß 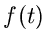 eine Funktion ist, deren Laplace-
Transformierte gleich
eine Funktion ist, deren Laplace-
Transformierte gleich 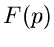 ist. Während die Laplace- Transformation
selbst im allgemeinen rechentechnisch einfach ist, bereitet die
Rücktransformation häufig Schwierigkeiten.
ist. Während die Laplace- Transformation
selbst im allgemeinen rechentechnisch einfach ist, bereitet die
Rücktransformation häufig Schwierigkeiten.
Beispiele.
Einige einfache Beispiele mögen diese Zuordnung veranschaulichen.
Sei 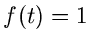 , dann ist
, dann ist
Wir schreiben also:
Für
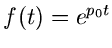 erhalten wir entsprechend
erhalten wir entsprechend
Bei diesem Integral muß man etwas Obacht geben. Wir zerlegen 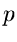 und
und
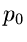 in Real- und Imaginärteil,
in Real- und Imaginärteil,
Dieses Integral ist dann und nur dann endlich und gleich
wenn
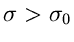 . Wir erhalten also die Zuordnung
. Wir erhalten also die Zuordnung
Allgemeiner kann man nachrechnen, daß
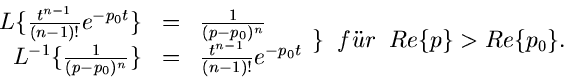 |
(8) |
Die beiden ersten Beispiele sind als Spezialfälle in diesem letzteren
Beispiel enthalten.
Transformationsregeln.
Die folgenden Regeln lassen sich aus der Integraldefinition der Laplace-
Transformation herleiten:
Linearität:
Differentiation und Integral:
Verschiebungssatz:
 |
(13) |
Faltungssatz:
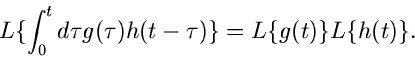 |
(14) |
Besonders die Regeln für die Integrale und Ableitungen muß man sich
auf der Zunge zergehen lassen. Hier wird die komplizierte Operation
eines Integrals oder einer Ableitung im Originalbereich ersetzt durch
einfache algebraische Operationen im Bildbereich. Die Beweise für diese
Regeln überlassen wir dem Leser (Stichwort: partielle Integration).
Beispiel.
Wir wollen die Transformationsregeln an einigen Beispielen erläutern.
Gegeben sei die Zeitfunktion (siehe Abb.1)
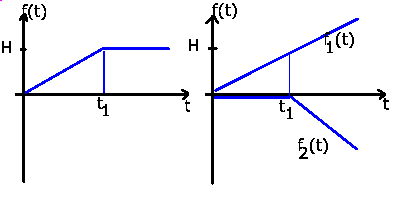
Abbildung 1:
Einfache Zeitfunktion.
Wir zerlegen die Funktion in zwei Teile (siehe rechte Seite von Abb.1):
Dann ist
und
Dabei ist gemäß Formel (8) (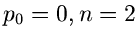 ):
):
Mit Hilfe des Verschiebungssatzes erhalten wir:
Das Endergebnis lautet:
Beispiel.
Die Schaltfunktion kann dargestellt werden als
wobei  die Sprungfunktion
die Sprungfunktion
ist. Die zu  gehörige Bildfunktion ist
gehörige Bildfunktion ist
sodaß mit Hilfe des Verschiebungssatzes folgt:
Beispiel.
Gegeben sei ein Rechteckimpuls (siehe Abb.2):
wobei 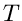 eine feste Zeit und
eine feste Zeit und 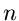 irgendeine positive Zahl ist.
irgendeine positive Zahl ist.
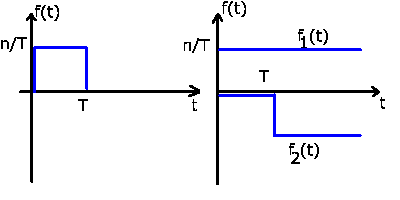
Abbildung 2:
Zerlegung des Rechteckimpulses in zwei Teilfunktionen.
 läßt sich als Summe zweier Schaltfunktionen darstellen:
läßt sich als Summe zweier Schaltfunktionen darstellen:
Die Laplace- Transformierte lautet:
Wir entwickeln den Ausdruck in der eckigen Klammer,
Für große  können wir alle weiteren Glieder vernachlässigen. Im
Grenzfall
können wir alle weiteren Glieder vernachlässigen. Im
Grenzfall 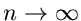 folgt:
folgt:
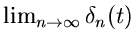 ist aber nichts anderes als die
Diracsche
ist aber nichts anderes als die
Diracsche 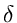 - Funktion, sodaß wir schreiben können
- Funktion, sodaß wir schreiben können
In einer etwas allgemeineren Form gilt dann:
Inverse Transformation
Während die Laplace- Transformation selbst und das Rechnen im Bildbereich
recht einfach sind, kann die inverse Transformation erhebliche
Schwierigkeiten bereiten. Zur Lösung wird man zunächst versuchen, durch
,,raten'' oder ,,probieren'' die zu 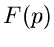 gehörige Originalfunktion
gehörige Originalfunktion
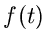 zu finden. Besonders hilfreich sind hierbei die in der Literatur
vorhandenen Korrespondenztabellen. Eine andere Möglichkeit ist die
Rücktransformation mit Hilfe des Faltungssatzes:
zu finden. Besonders hilfreich sind hierbei die in der Literatur
vorhandenen Korrespondenztabellen. Eine andere Möglichkeit ist die
Rücktransformation mit Hilfe des Faltungssatzes:
 |
(15) |
Wenn es also möglich ist, die Bildfunktion 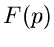 so in zwei Faktoren
so in zwei Faktoren
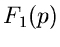 und
und 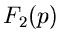 zu zerlegen, daß diese einzeln leicht
rücktransformierbar sind, erhält man eine Integraldarstellung der
Originalfunktion
zu zerlegen, daß diese einzeln leicht
rücktransformierbar sind, erhält man eine Integraldarstellung der
Originalfunktion
 |
(16) |
Wenn alle diese Methoden versagen, muß man zum folgenden immer anwendbaren
Algorithmus übergehen.
Umkehrformel.
Die Funktion 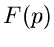 habe singuläre Stellen in endlich vielen Punkten
habe singuläre Stellen in endlich vielen Punkten
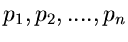 .
. 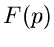 sei insbesondere regulär im Punkte
sei insbesondere regulär im Punkte
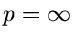 . Für einen Punkt
. Für einen Punkt 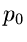 außerhalb des geschlossenen
Weges
außerhalb des geschlossenen
Weges 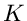 um die singulären Punkte gilt dann nach Formel (53) des vorherigen Kapitels:
um die singulären Punkte gilt dann nach Formel (53) des vorherigen Kapitels:
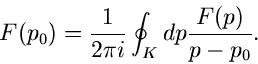 |
(17) |
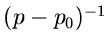 ist nun aber eine Bildfunktion, nämlich
ist nun aber eine Bildfunktion, nämlich
Die Vertauschung der Vorzeichen in den Exponentialausdrücken ist nicht
unbedingt einleuchtend, soll hier aber ohne Beweis übergangen werden.
Wir setzen dieses in (17) ein und erhalten nach Vertauschen der
Integrationsreihenfolge (ungeachtet dessen, ob diese Vertauschung erlaubt
ist oder nicht, siehe späteren Kommentar):
Ein Vergleich mit der Laplace- Transformation zeigt, daß
sein muß. Mit Hilfe der Residuenformel des vorherigen Kapitels
folgt:
 |
(18) |
Das ganze Problem der Rücktransformation reduziert sich mit dieser Formel
darauf, die singulären Stellen des Ausdrucks  zu berechnen
und zu summieren. Die Umkehrformel wurde abgeleitet, ohne auf einige
mathematisch notwendige Bedingungen einzugehen. Das so erhaltene Ergebnis
kann daher auch falsch sein. Man muß also immer noch einmal prüfen, ob
die berechnete Funktion
zu berechnen
und zu summieren. Die Umkehrformel wurde abgeleitet, ohne auf einige
mathematisch notwendige Bedingungen einzugehen. Das so erhaltene Ergebnis
kann daher auch falsch sein. Man muß also immer noch einmal prüfen, ob
die berechnete Funktion 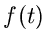 wirklich die Originalfunktion zu
wirklich die Originalfunktion zu 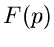 ist.
Für eine besonders häufig vorkommende Funktionenklasse, nämlich für die
rationalen Funktionen, die im Unendlichen verschwinden, funktioniert
diese Rücktransformation aber immer und liefert auch die richtige
Originalfunktion.
ist.
Für eine besonders häufig vorkommende Funktionenklasse, nämlich für die
rationalen Funktionen, die im Unendlichen verschwinden, funktioniert
diese Rücktransformation aber immer und liefert auch die richtige
Originalfunktion.
Beispiel.
Zur Demonstrartion diskutieren wir zwei einfache Anwendungen aus der Elektrotechnik.
Gegeben sei der Schaltkreis in Abbildung 3.
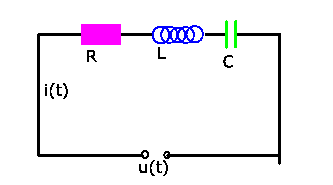
Abbildung 3:
Elektrisches Schaltkreis mit Widerstand, Spule und Kondensator.
Aus den Gesetzen der Elektrotechnik entnehmen wir die folgende Beziehung
zwischen Strom  und Spannung
und Spannung 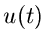 :
:
Anwendung der Laplace- Transformation liefert:
Hierbei wurde
gesetzt. Außerdem ist 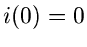 , sofern
, sofern 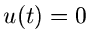 für
für 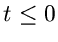 gesetzt
wird. Die Lösung im Bildraum ist
gesetzt
wird. Die Lösung im Bildraum ist
mit
und
Die Transformation und Lösung im Bildraum ist also außerordentlich
einfach. Das Problem ist die Rücktransformation. Mit Hilfe des Faltungssatzes
ergibt sich
Da 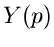 eine rationale Funktion ist, die im Unendlichen verschwindet, kann
eine rationale Funktion ist, die im Unendlichen verschwindet, kann
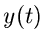 mit Hilfe der Residuenformel zurücktransformiert werden,
mit Hilfe der Residuenformel zurücktransformiert werden,
Die Residuen in den beiden Polen sind
sodaß wir die allgemeine Lösung schreiben können als
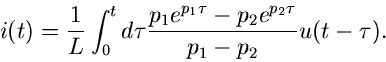 |
(19) |
Dieses ist ein relles Integral, was man folgendermaßen einsehen kann.
Wenn 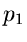 und
und 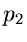 reell sind, ist (19) in jedem Fall reell.
Seien
reell sind, ist (19) in jedem Fall reell.
Seien 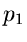 und
und 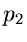 komplex, so sind
komplex, so sind 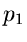 und
und 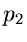 konjugiert
komplex zueinander, also
konjugiert
komplex zueinander, also
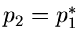 . Nach den Formeln für
komplex konjugierte Zahlen erhalten wir nach einiger Rechnung
. Nach den Formeln für
komplex konjugierte Zahlen erhalten wir nach einiger Rechnung
wobei wir
gesetzt haben. Wenn 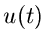 nicht zu kompliziert ist, kann man dieses Integral
elementar lösen. Wenn dagegen
nicht zu kompliziert ist, kann man dieses Integral
elementar lösen. Wenn dagegen 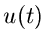 einen gewissen Kompliziertheitsgrad
übersteigt, muß man numerisch integrieren.
einen gewissen Kompliziertheitsgrad
übersteigt, muß man numerisch integrieren.
Beispiel.
In einem zweiten Beispiel der Elektrotechnik sei der Stromkreis von Abb.4
gegeben.
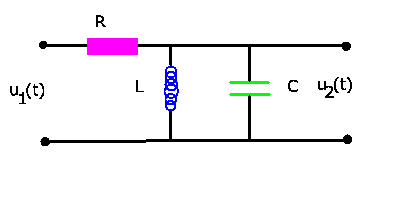
Abbildung 4:
Eine einfache Vierpol- Schaltung.
Gesucht ist die Spannung 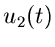 als Funktion der Spannung
als Funktion der Spannung 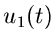 .
Offensichtlich ist
.
Offensichtlich ist
Wir eliminieren die Ströme und erhalten folgende Gleichung zwischen
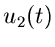 und
und 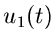 :
:
Anwendung der Laplace- Transformation ergibt
oder
mit
Alles weitere geht wie im ersten Beispiel. Wir schreiben
und erhalten mit Hilfe des Faltungssatzes
mit
Nach einiger Rechnung folgt das Resultat
Auch in dieser Formel kann man sich davon überzeugen, daß, obwohl
komplexe Zahlen in den Formeln stehen, die Spannung 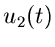 eine reelle
Funktion ist. Wir erhalten wie im vorigen Beispiel das reelle Integral
eine reelle
Funktion ist. Wir erhalten wie im vorigen Beispiel das reelle Integral
mit
Mehrdimensionale Laplace- Transformation
Für eine Funktion 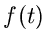 hatten wir die (einseitige) Laplace- Transformation
definiert als
hatten wir die (einseitige) Laplace- Transformation
definiert als
Diese Definition kann man ohne weiteres verallgemeinern für den Fall einer
Funktion 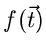 mehrerer Veränderlicher
mehrerer Veränderlicher
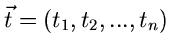 :
:
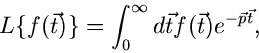 |
(20) |
mit dem komplexen Vektor
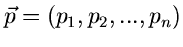 . Leider ist
die Theorie der komplexen Funktionen mehrerer Veränderlicher um einiges
schwieriger zu handhaben als die Theorie der komplexen Funktionen mit nur
einer Veränderlichen. Wir können die Theorie der mehrdimensionalen
komplexen Funktionen jedoch umgehen, wenn wir die Transformation (20)
schreiben in der Form
. Leider ist
die Theorie der komplexen Funktionen mehrerer Veränderlicher um einiges
schwieriger zu handhaben als die Theorie der komplexen Funktionen mit nur
einer Veränderlichen. Wir können die Theorie der mehrdimensionalen
komplexen Funktionen jedoch umgehen, wenn wir die Transformation (20)
schreiben in der Form
Definieren wir die Laplace Transformierte bezüglich der Variablen 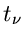 durch
durch
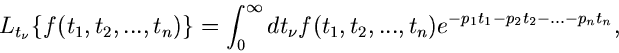 |
(21) |
so kann man schreiben:
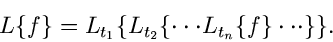 |
(22) |
Für jeden einzelnen Transformationsschritt kann der gesamte Formalismus
der eindimensionalen Laplace Transformation angewendet werden.
Korrespondenztabellen.
Bisher haben wir in unseren Beispielen alle Rücktransformationen
mit Hilfe des Verschiebungssatzes, des Faltungssatzes oder der Residuenformel
lösen können. In einer ganzen Reihe von Anwendungen sind diese Verfahren
jedoch außerordentlich mühsam und zeitraubend. Man bedient sich daher
zweckmäßigerweise der Korrespondenztabellen, in denen ähnlich wie in
einer Integraltafel alle nur denkbaren Laplace- Transformationen
tabelliert sind. Diese Korrespondenztabellen gehören selbstverständlich
auf den Schreibtisch eines jeden Systemanalytikers. Auch wir werden
im folgenden häufig von diesen Korrespondenztabellen Gebrauch machen.
Fourier Transformation
Die Integraltransformation
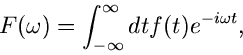 |
(23) |
wobei 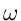 reell ist, führt auf den Begriff der Fourier Transformation.
Die Operator Schreibweise ist
reell ist, führt auf den Begriff der Fourier Transformation.
Die Operator Schreibweise ist
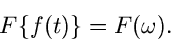 |
(24) |
Um die Umkehrrelation zu erhalten, multiplizieren wir  mit
mit
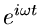 und integrieren über
und integrieren über 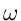 . Nach Einsetzen von
. Nach Einsetzen von
 aus (23) erhalten wir
aus (23) erhalten wir
Das rechts stehende Integral ist nun aber gerade die Diracsche 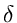 -
Funktion:
-
Funktion:
Daher folgt
 |
(25) |
Die Bildfunktion der Laplace Transformation ist eine komplexwertige Funktion
einer komplexen Veränderlichen. Im Gegensatz dazu ist die Bildfunktion der
Fourier Transformation eine komplexwertige Funktion einer reellen
Veränderlichen.
Rechenregeln.
Die wichtigsten Rechenregeln der Fourier Transformation sind:
Linearität:
Ableitung und Integral:
Faltungssatz:
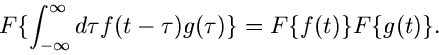 |
(30) |
Verschiebungssatz:
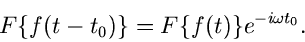 |
(31) |
Wir bemerken insbesondere das Fehlen des Anfangswertes 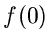 in der Regel
für die Ableitung. Die Anfangswertbedingung
in der Regel
für die Ableitung. Die Anfangswertbedingung 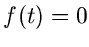 für
für
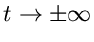 ist jedoch bereits in der Bedingung für die Existenz des Fourier Integrals
enthalten. Das Integral existiert nur, wenn
ist jedoch bereits in der Bedingung für die Existenz des Fourier Integrals
enthalten. Das Integral existiert nur, wenn 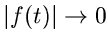 für
für
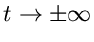 . Dieser Sachverhalt führt uns auf den großen Nachteil
der Fourier Transformation, nämlich ihre Konvergenzempfindlichkeit.
Die (zweiseitige) Laplace Transformation war definiert als
(mit
. Dieser Sachverhalt führt uns auf den großen Nachteil
der Fourier Transformation, nämlich ihre Konvergenzempfindlichkeit.
Die (zweiseitige) Laplace Transformation war definiert als
(mit
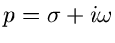 ):
):
wogegen in der Fourier Transformation der Dämpfungsterm 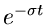 fehlt:
fehlt:
Bei der Fourier Transformation muß die Existenz des Integrals von der
Funktion 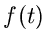 allein zuwege gebracht werden, während bei der Laplace
Transformation der Faktor
allein zuwege gebracht werden, während bei der Laplace
Transformation der Faktor 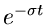 für fast alle Funktionen
für fast alle Funktionen 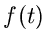 die Existenz des Integrals garantiert, sofern nur
die Existenz des Integrals garantiert, sofern nur 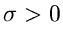 bzw
bzw
 . Die Menge der Funktionen
. Die Menge der Funktionen 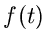 , die eine Fourier
Transformierte besitzen, ist gegenüber der Laplace Transformation erheblich
eingeschränkt. Wegen des Fehlens einer frei wählbaren Anfangsbedingung
ist die Fourier Transformation in der Systemanalyse nur beschränkt
einsetzbar. Für Untersuchungen des Einschwingverhaltens ist die Fourier
Transformation sogar ungeeignet. Dagegen erweist sie sich häufig der Laplace
Transformation überlegen, wenn man den eingeschwungenen Zustand bei
periodischer Erregung zu untersuchen hat.
, die eine Fourier
Transformierte besitzen, ist gegenüber der Laplace Transformation erheblich
eingeschränkt. Wegen des Fehlens einer frei wählbaren Anfangsbedingung
ist die Fourier Transformation in der Systemanalyse nur beschränkt
einsetzbar. Für Untersuchungen des Einschwingverhaltens ist die Fourier
Transformation sogar ungeeignet. Dagegen erweist sie sich häufig der Laplace
Transformation überlegen, wenn man den eingeschwungenen Zustand bei
periodischer Erregung zu untersuchen hat.
Abtasttheorem
Es sei 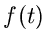 eine beliebige Zeitfunktion mit einer Fourier Transformierten
eine beliebige Zeitfunktion mit einer Fourier Transformierten
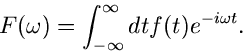 |
(32) |
Wegen
 ist
ist 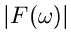 symmetrisch um
symmetrisch um
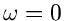 , d.h.
, d.h.
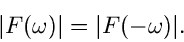 |
(33) |
Man nennt die Funktion 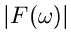 das Spektrum der Funktion
das Spektrum der Funktion 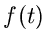 .
Die Funktion
.
Die Funktion 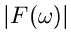 muß nun, genau wie die Funktion
muß nun, genau wie die Funktion 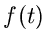 , für
, für
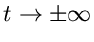 gegen Null konvergieren. Dieses folgt aus der Existenz des
Umkehrintegrals. Ab einem gewissen Wert
gegen Null konvergieren. Dieses folgt aus der Existenz des
Umkehrintegrals. Ab einem gewissen Wert
 ist nun
ist nun 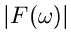 so klein, daß man
so klein, daß man
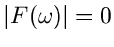 für
für
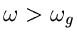 setzen kann.
Wir nennen die zugehörige Zeitfunktion
setzen kann.
Wir nennen die zugehörige Zeitfunktion
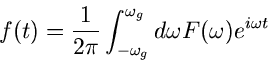 |
(34) |
ein Signal mit bandbegrenztem Spektrum. Die Berechtigung für diese
Approximation liegt darin, daß alle in der Natur vorkommenden Signale
ein bandbegrenztes Spektrum besitzen. Diese Bemerkung gilt erst recht
für alle in experimentellen Anordnungen gemessenen Signale. Formel (34)
ist die Definitionsgleichung für die Rücktransformation bei einem
bandbegrenzten Spektrum.
Benutzt man (34) als Formel für die Rücktransformation, so kann
 für
für
 beliebig fortgesetzt werden,
z.B. periodisch mit
beliebig fortgesetzt werden,
z.B. periodisch mit
In diesem Fall kann man  durch eine sogenannte Fourier Reihe
darstellen,
durch eine sogenannte Fourier Reihe
darstellen,
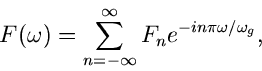 |
(35) |
wobei die Koeffizienten 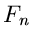 für die Konvergenz verantwortlich sind,
d.h.
für die Konvergenz verantwortlich sind,
d.h.
Zur Bestimmung der Koeffizienten 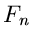 multiplizieren wir (35) mit
multiplizieren wir (35) mit
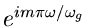 und integrieren von
und integrieren von 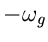 bis
bis
 :
:
Das rechts stehende Integral läßt sich wieder durch die 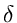 - Funktion
ausdrücken,
- Funktion
ausdrücken,
Daher folgt
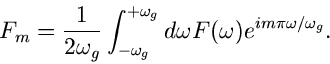 |
(36) |
Ein Vergleich mit (34) zeigt, daß
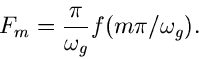 |
(37) |
Wir setzen jetzt die Fourier- Reihe (35) mit den Entwicklungskoeffizienten
(37) in die Formel (34) für die Rücktransformation ein. Dieses
ergibt:
oder, sofern wir Summe und Integral vertauschen dürfen,
Das rechts stehende Integral läßt sich elementar ausrechnen. Setzen wir
zur Abkürzung noch
 , so ergibt sich schließlich
die sogenannte Sampling- Reihe.
, so ergibt sich schließlich
die sogenannte Sampling- Reihe.
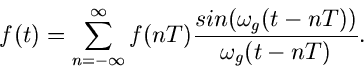 |
(38) |
Diese Formel läßt sich mit folgendem Satz (Abtasttheorem)
interpretieren:
Besitzt eine Zeitfunktion 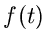 ein bandbegrenztes Spektrum mit der
oberen Grenzfrequenz
ein bandbegrenztes Spektrum mit der
oberen Grenzfrequenz 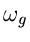 , dann ist
, dann ist 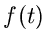 durch die diskreten
Tastwerte
durch die diskreten
Tastwerte 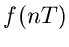 mit
mit
 vollständig bestimmt. Die
Fourier- Transformierte dieser bandbegrenzten Zeitfunktion ist
vollständig bestimmt. Die
Fourier- Transformierte dieser bandbegrenzten Zeitfunktion ist
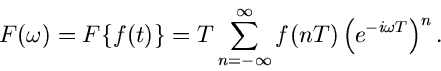 |
(39) |
Eine solche Funktionsdarstellung durch diskrete Abtastwerte ist nun aber
wesentlich besser sowohl für experimentelle wie für rechentechnische
Anwendungen geeignet als eine kontinuierliche Funktion. Insbesondere kann
man wegen 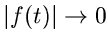 und
und
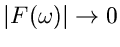 für
für
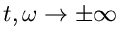 die Summe durch eine endliche Summe approximieren.
die Summe durch eine endliche Summe approximieren.
Laurent- und Z- Transformation
Nach dem Vorbild des Abtasttheorems wird die Laurent- Transformation
definiert als
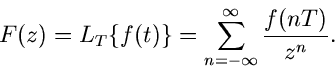 |
(40) |
Falls  für
für 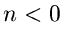 , so gelangt man zur Z- Transformation
, so gelangt man zur Z- Transformation
 |
(41) |
Die Z- Transformation ist also als Spezialfall in der Laurent- Transformation
enthalten. Wir werden daher alle Formeln nur für die Laurent- Transformation
herleiten.
Rücktransformation.
Zur Rücktransformation erwähnen wir zwei häufig benuzte Methoden.
Die erste Methode basiert auf der Laurent- Reihenentwicklung (daher der
Name dieser Transformation). Hierzu wird die Bildfunktion 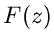 in eine
Potenzreihe um
in eine
Potenzreihe um 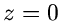 entwickelt:
entwickelt:
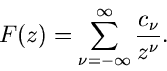 |
(42) |
Durch Vergleich mit (40) erkennt man sofort, daß
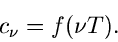 |
(43) |
Ist die Bildfunktion insbesondere rational in 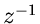 , d.h.
, d.h.
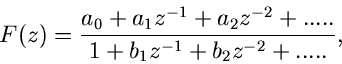 |
(44) |
so erhält man die Koeffizienten
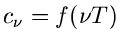 aus der einfachen
Rekursionsrelation
aus der einfachen
Rekursionsrelation
Die zweite Methode basiert auf der Integralformel von Cauchy. Wir bilden
und berechnen das Kreisintegral um 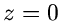 :
:
Das rechts stehende Integral ist aber nur für 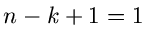 , d.h. für
, d.h. für
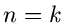 , von Null verschieden,
, von Null verschieden,
Daher folgt die Residuenformel der Laurent- Rücktransformation:
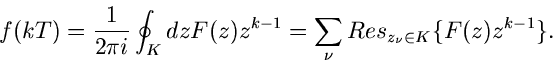 |
(46) |
Diese Formel ist vollkommen equivalent zur Residuenformel der Laplace
Transformation.
Rechenregeln.
Ausgehend von den Rechenregeln der Fourier Transformation und mit Hilfe
der Relation
lassen sich folgende Regeln herleiten:
Linearität:
Ableitung und Integral:
mit
![\begin{displaymath}
\psi(z) = \frac{1}{T} ln z = \frac{2}{T} \left[ \frac{z-1}{z...
...}{3} \frac{(z-1)^{3}}{(z+1)^{3}} + \cdot \cdot \cdot \right] .
\end{displaymath}](img238.gif) |
(51) |
In praktischen Anwendungen kann im allgemeinen
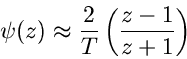 |
(52) |
gesetzt werden. Die gleichen Relationen gelten natürlich für die
Z- Transformation mit  für
für  .
.
Wir möchten noch auf die Ähnlichkeit der Rechenregeln der Laplace- und
der Laurent- Transformation hinweisen. Man muß nur  durch
durch  ersetzen und beachten, daß die Anfangsbedingung
ersetzen und beachten, daß die Anfangsbedingung 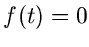 für
für 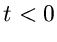 bei der (einseitigen) Laplace- Transformation durch
bei der (einseitigen) Laplace- Transformation durch 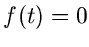 für
für
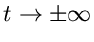 bei der Laurent- Transformation ersetzt wurde.
bei der Laurent- Transformation ersetzt wurde.
Harm Fesefeldt
2006-04-05


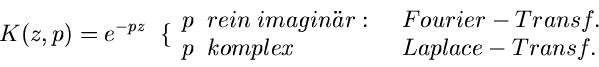
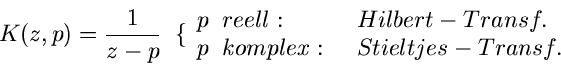
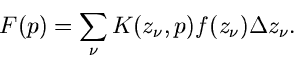
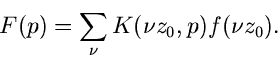
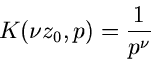
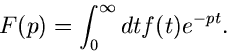
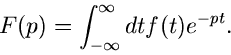

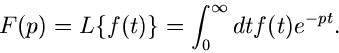
![]() , dann ist
, dann ist
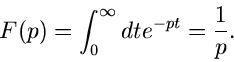
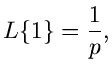
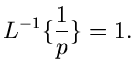
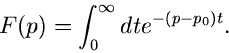
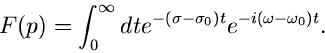
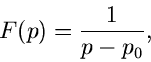
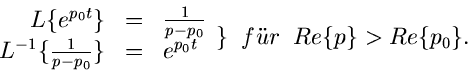
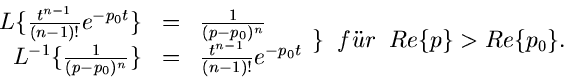
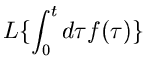
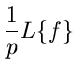
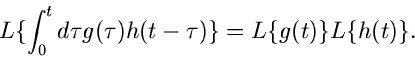
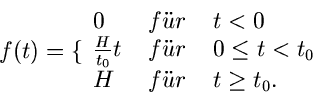

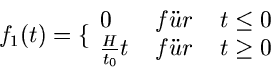

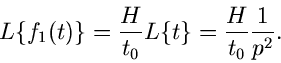
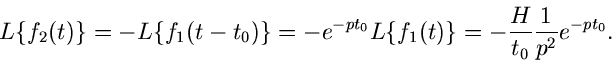
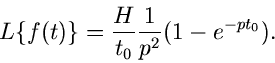
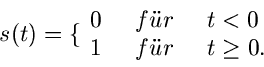
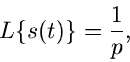



![]() läßt sich als Summe zweier Schaltfunktionen darstellen:
läßt sich als Summe zweier Schaltfunktionen darstellen:
![\begin{displaymath}
\delta_{n}(t) = \frac{n}{T} [ s(t) - s(t - \frac{T}{n}) ].
\end{displaymath}](img73.gif)
![\begin{displaymath}
L \{ \delta_{n}(t) \} = \frac{n}{pT} \left[ 1 - e^{-pT/n} \right] .
\end{displaymath}](img74.gif)
![\begin{displaymath}
L \{ \delta_{n} \} = \frac{n}{pT} \frac{pT}{n} \left[ 1 - \frac{1}{2!}
\frac{pT}{n} + \cdot \cdot \cdot \right].
\end{displaymath}](img75.gif)
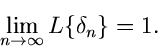
![]() gehörige Originalfunktion
gehörige Originalfunktion
![]() zu finden. Besonders hilfreich sind hierbei die in der Literatur
vorhandenen Korrespondenztabellen. Eine andere Möglichkeit ist die
Rücktransformation mit Hilfe des Faltungssatzes:
zu finden. Besonders hilfreich sind hierbei die in der Literatur
vorhandenen Korrespondenztabellen. Eine andere Möglichkeit ist die
Rücktransformation mit Hilfe des Faltungssatzes:


![]() habe singuläre Stellen in endlich vielen Punkten
habe singuläre Stellen in endlich vielen Punkten
![]() .
. ![]() sei insbesondere regulär im Punkte
sei insbesondere regulär im Punkte
![]() . Für einen Punkt
. Für einen Punkt ![]() außerhalb des geschlossenen
Weges
außerhalb des geschlossenen
Weges ![]() um die singulären Punkte gilt dann nach Formel (53) des vorherigen Kapitels:
um die singulären Punkte gilt dann nach Formel (53) des vorherigen Kapitels:
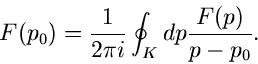

![\begin{displaymath}
F(p_{0}) = \int_{0}^{\infty} dt e^{-p_{0}t} \left[ \frac{1}{2 \pi i}
\oint_{K} dp F(p) e^{pt} \right] .
\end{displaymath}](img92.gif)
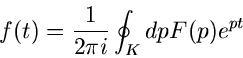


![]() und Spannung
und Spannung ![]() :
:
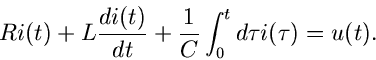
![\begin{displaymath}
I(p) [ R + pL + \frac{1}{pC} ] = U(p).
\end{displaymath}](img99.gif)
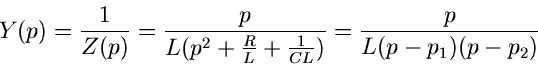
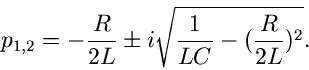
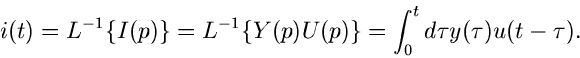
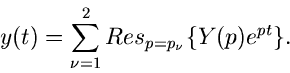
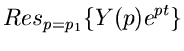

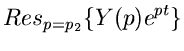
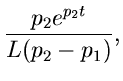
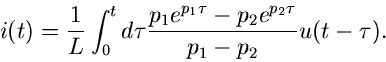
![]() und
und ![]() reell sind, ist (19) in jedem Fall reell.
Seien
reell sind, ist (19) in jedem Fall reell.
Seien ![]() und
und ![]() komplex, so sind
komplex, so sind ![]() und
und ![]() konjugiert
komplex zueinander, also
konjugiert
komplex zueinander, also
![]() . Nach den Formeln für
komplex konjugierte Zahlen erhalten wir nach einiger Rechnung
. Nach den Formeln für
komplex konjugierte Zahlen erhalten wir nach einiger Rechnung
![\begin{displaymath}
i(t) = \frac{1}{\omega L} \int_{0}^{t} d\tau e^{\sigma \tau}...
...sigma sin(\omega \tau) + \omega cos(\omega \tau) ] u(t-\tau) ,
\end{displaymath}](img119.gif)

![]() als Funktion der Spannung
als Funktion der Spannung ![]() .
Offensichtlich ist
.
Offensichtlich ist

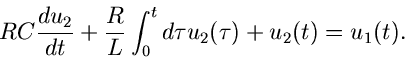
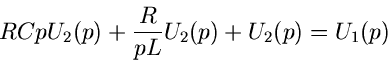
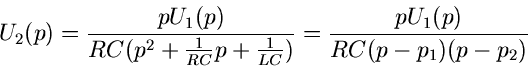
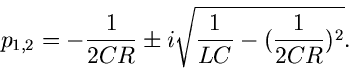
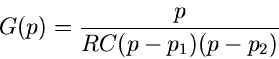
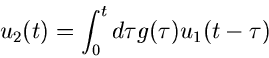

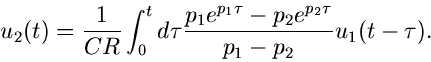
![\begin{displaymath}
u_{2}(t) = \frac{1}{\omega CR} \int_{0}^{t} d\tau e^{\sigma ...
...gma sin(\omega \tau) + \omega cos(\omega \tau) ] u_{1}(t-\tau)
\end{displaymath}](img137.gif)
![]() hatten wir die (einseitige) Laplace- Transformation
definiert als
hatten wir die (einseitige) Laplace- Transformation
definiert als

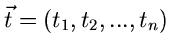 :
:
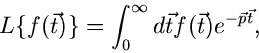
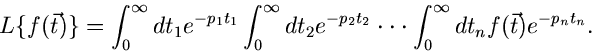
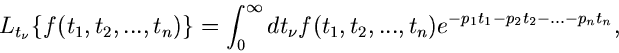
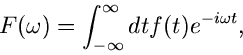
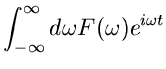
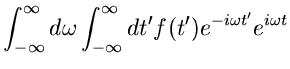
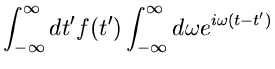
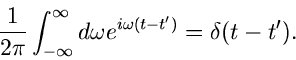

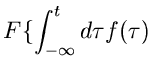
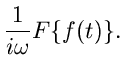
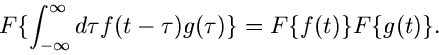
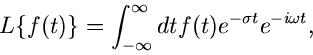
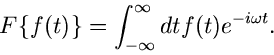
![]() eine beliebige Zeitfunktion mit einer Fourier Transformierten
eine beliebige Zeitfunktion mit einer Fourier Transformierten
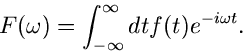
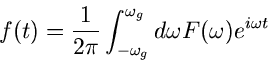
![]() für
für
![]() beliebig fortgesetzt werden,
z.B. periodisch mit
beliebig fortgesetzt werden,
z.B. periodisch mit
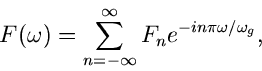
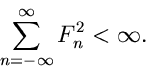
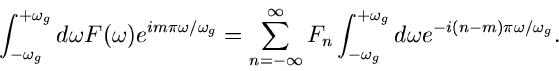
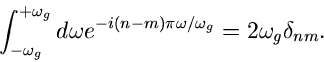
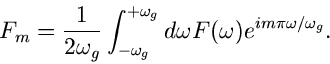
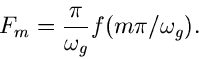
![\begin{displaymath}
f(t) = \frac{1}{2 \pi} \int_{-\omega_{g}}^{+\omega_{g}} d\om...
...{g})
e^{-i n \pi \omega / \omega_{g}} \right] e^{i \omega t} ,
\end{displaymath}](img199.gif)
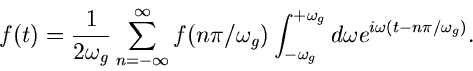
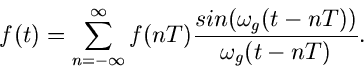
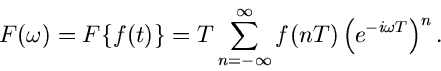
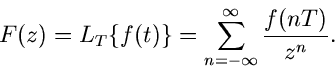

![]() in eine
Potenzreihe um
in eine
Potenzreihe um ![]() entwickelt:
entwickelt:
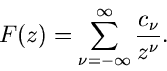
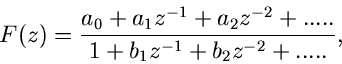
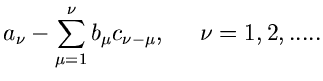

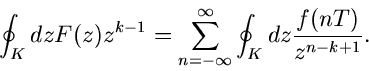

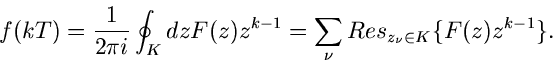
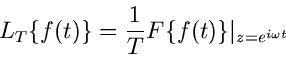
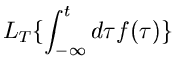
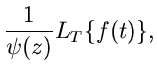
![\begin{displaymath}
\psi(z) = \frac{1}{T} ln z = \frac{2}{T} \left[ \frac{z-1}{z...
...}{3} \frac{(z-1)^{3}}{(z+1)^{3}} + \cdot \cdot \cdot \right] .
\end{displaymath}](img238.gif)
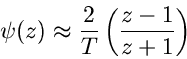
![]() durch
durch ![]() ersetzen und beachten, daß die Anfangsbedingung
ersetzen und beachten, daß die Anfangsbedingung ![]() für
für ![]() bei der (einseitigen) Laplace- Transformation durch
bei der (einseitigen) Laplace- Transformation durch ![]() für
für
![]() bei der Laurent- Transformation ersetzt wurde.
bei der Laurent- Transformation ersetzt wurde.