Messung der Wahrscheinlichkeit
Bernoulli- Verteilung
In diesem Abschnitt werden wir ein wichtiges Ergebnis der Statistik
diskutieren, nämlich die Formel von Bernoulli. Diese Formel wird uns
dann in die Lage versetzen, eine Methode zur Bestimmung von
Wahrscheinlichkeiten zu diskutieren. Gegeben sei ein Versuch V. Wir
interessieren uns nur für das Ereignis  und das dazu komplementäre
Ereignis
und das dazu komplementäre
Ereignis 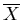 . Wir schreiben für die Wahrscheinlichkeiten
. Wir schreiben für die Wahrscheinlichkeiten
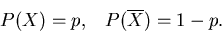 |
(1) |
Wir führen den Versuch n- mal aus und fragen nach der Wahrscheinlichkeit,
daß bei n- maliger Ausführung des Versuches k- mal das Ereignis  eintritt und (n-k)- mal das Ereignis
eintritt und (n-k)- mal das Ereignis 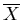 . Diese Wahrscheinlichkeit
bezeichnen wir mit
. Diese Wahrscheinlichkeit
bezeichnen wir mit 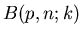 . Für n=1 gilt offenbar
. Für n=1 gilt offenbar
Dieses entspricht genau der Annahme, die wir oben gemacht haben.
Bei mehrmaliger Ausführung ist das Eintreten des Ereignisses  unabhängig
von den Ereignissen der vorhergehenden Versuche.
Für n=2, d.h. bei zweimaliger Ausführung des
Versuches, gibt es 4 Möglichkeiten, siehe Tabelle 1.
unabhängig
von den Ereignissen der vorhergehenden Versuche.
Für n=2, d.h. bei zweimaliger Ausführung des
Versuches, gibt es 4 Möglichkeiten, siehe Tabelle 1.
Tabelle 1:
Wahrscheinlichkeiten für das Ereignis  bei zweimaliger Durchführung eines
Versuches.
bei zweimaliger Durchführung eines
Versuches.
| Möglichkeit |
1. Versuch |
2. Versuch |
k |
Wahrscheinlichkeit |
| |
|
|
|
|
| 1 |
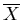 |
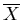 |
0 |
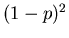 |
| 2 |
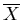 |
 |
1 |
 |
| 3 |
 |
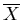 |
1 |
 |
| 4 |
 |
 |
2 |
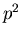 |
Die Wahrscheinlichkeiten für das Eintreten der Möglichkeiten 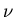
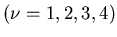 bei 2 Versuchen ist in der rechten Spalte der Tabelle
aufgeführt. Hieraus ergibt sich
bei 2 Versuchen ist in der rechten Spalte der Tabelle
aufgeführt. Hieraus ergibt sich
Dieses können wir schreiben als
Durch Induktion erhält man die allgemeine Formel von Bernoulli:
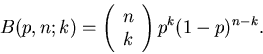 |
(2) |
Wir könnten den soeben diskutierten Sachverhalt auch folgendermaßen
ausdrücken. Unser Versuch 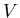 besteht aus n Einzelversuchen
besteht aus n Einzelversuchen 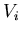
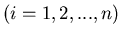 . Wir definieren die Ereignisse
. Wir definieren die Ereignisse 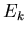 dadurch, daß
wir sagen,
dadurch, daß
wir sagen, 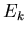 ist eingetreten, wenn bei n Einzelversuchen k- mal
das Ereignis
ist eingetreten, wenn bei n Einzelversuchen k- mal
das Ereignis  eintritt. Die Ereignisse
eintritt. Die Ereignisse 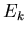
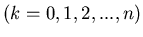 sind paarweise unvereinbar, sind also ein Satz von Elementarereignissen.
Wir ordnen jedem Elementarereignis
sind paarweise unvereinbar, sind also ein Satz von Elementarereignissen.
Wir ordnen jedem Elementarereignis 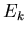 eine Wahrscheinlichkeit
eine Wahrscheinlichkeit
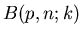 zu. Diese kann gemäß (2) durch die Wahrscheinlichkeit
zu. Diese kann gemäß (2) durch die Wahrscheinlichkeit
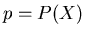 für das Auftreten des Ereignisses
für das Auftreten des Ereignisses  im Einzelversuch
ausgedrückt werden.
im Einzelversuch
ausgedrückt werden.
Wir prüfen die Normierung der Bernoulli- Formel gemäß
Die Berechnung der Formel ist am einfachsten mit Hilfe der Rekursionen
Für nicht zu große Werte von n kann man mit 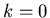 als Startwert
der Rekursion beginnen,
als Startwert
der Rekursion beginnen,
Für 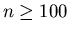 dagegen sollte man mit demjenigen k- Wert als
Startwert beginnen, bei dem die Bernoulli- Verteilung ihr Maximum
annimmt. Es ist nicht schwer zu ,,raten'', daß das Maximum in der
Nähe des Wertes
dagegen sollte man mit demjenigen k- Wert als
Startwert beginnen, bei dem die Bernoulli- Verteilung ihr Maximum
annimmt. Es ist nicht schwer zu ,,raten'', daß das Maximum in der
Nähe des Wertes
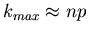 liegt.
liegt. 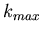 kann natürlich
nicht exakt bei
kann natürlich
nicht exakt bei 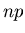 liegen, da
liegen, da  eine ganze Zahl und
eine ganze Zahl und 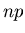 im allgemeinen
eine reelle Zahl ist. Für einen beliebigen Wert von
im allgemeinen
eine reelle Zahl ist. Für einen beliebigen Wert von  berechnet man die
Bernoulli- Formel am besten über den Logarithmus. Es ist
berechnet man die
Bernoulli- Formel am besten über den Logarithmus. Es ist
 |
(5) |
In einem Programm berechnen wir zunächst den
Funktionswert für
 , wobei INT eine Systemfunktion ist, die
die größte ganze Zahl liefert mit
, wobei INT eine Systemfunktion ist, die
die größte ganze Zahl liefert mit
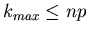 . Für diesen
. Für diesen  - Wert
berechnen wir die Bernoulli- Formel mit Hilfe von (5). Alle weiteren
Funktionswerte werden dann mit der Rekursion (3) und (4) berechnet.
Die Zahlenwerte dieser Rechnung sind für
- Wert
berechnen wir die Bernoulli- Formel mit Hilfe von (5). Alle weiteren
Funktionswerte werden dann mit der Rekursion (3) und (4) berechnet.
Die Zahlenwerte dieser Rechnung sind für 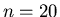 und
und 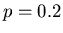 in
der zweiten Spalte von Tabelle 2 aufgelistet. Die übrigen Spalten
dieser Tabelle enthalten Ergebnisse von approximativen Formeln, die uns
im folgenden beschäftigen werden.
in
der zweiten Spalte von Tabelle 2 aufgelistet. Die übrigen Spalten
dieser Tabelle enthalten Ergebnisse von approximativen Formeln, die uns
im folgenden beschäftigen werden.
Die Rekursionsformel ist zwar gut für die Programmierung geeignet,
dagegen ist sie unbrauchbar für analytische Rechnungen, da  zunächst
nur für gerade Zahlen definiert ist. Eine Interpolationsformel
für reelle Zahlen erhält man mit Hilfe der Stirlingschen Formel
zunächst
nur für gerade Zahlen definiert ist. Eine Interpolationsformel
für reelle Zahlen erhält man mit Hilfe der Stirlingschen Formel
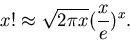 |
(6) |
Hiermit erhalten wir
und
Mit Hilfe eines zweiten kurzen Programms haben wir diese approximative
Darstellung der Bernoulli- Formel programmiert. In Tabelle 2 vergleichen wir
die Werte der Approximation mit denjenigen der exakten Formel (2) für
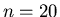 und
und 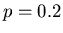 . Die Approximation ist für mittlere und große
k- Werte relativ gut, versagt dagegen völlig für kleine k- Werte.
Insbesondere darf man die Approximation nicht für kleine Werte von
. Die Approximation ist für mittlere und große
k- Werte relativ gut, versagt dagegen völlig für kleine k- Werte.
Insbesondere darf man die Approximation nicht für kleine Werte von 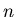 verwenden.
verwenden.
Tabelle:
Berechnung der Bernoulli- Verteilung für 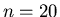 und
und 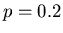 .
.
| k |
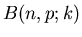 |
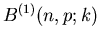 |
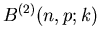 |
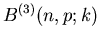 |
| |
|
|
|
|
| 0 |
0.011529 |
0.002300 |
0.026263 |
0.018306 |
| 1 |
0.057646 |
0.062527 |
0.071392 |
0.054652 |
| 2 |
0.136909 |
0.142754 |
0.141979 |
0.119372 |
| 3 |
0.205364 |
0.211283 |
0.206578 |
0.190755 |
| 4 |
0.218199 |
0.223016 |
0.219901 |
0.223016 |
| 5 |
0.174560 |
0.177736 |
0.171259 |
0.190755 |
| 6 |
0.109100 |
0.110822 |
0.097581 |
0.119372 |
| 7 |
0.054550 |
0.055327 |
0.040678 |
0.054652 |
| 8 |
0.022161 |
0.022455 |
0.012406 |
0.018306 |
| 9 |
0.007387 |
0.007481 |
0.002768 |
0.004486 |
| 10 |
0.002031 |
0.002057 |
0.000452 |
0.000804 |
| 11 |
0.000462 |
0.000468 |
0.000054 |
0.000106 |
| 12 |
0.000087 |
0.000088 |
0.000005 |
0.000010 |
| 13 |
0.000013 |
0.000014 |
0.000000 |
0.000001 |
| 14 |
0.000002 |
0.000002 |
0.000000 |
0.000000 |
|
Da uns die Bernoulli- Formel hauptsächlichst in der Nähe ihres Maximums
interessiert, führen wir die folgenden Parameter- und Variablen-
Transformationen ein:
Dann ist
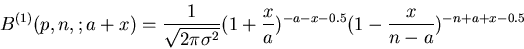 |
(10) |
Das Maximum dieser reellen Funktion ist, wie man leicht zeigen kann,
bei 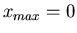 oder, wie wir oben schon vermutet haben, bei
einem k- Wert mit
oder, wie wir oben schon vermutet haben, bei
einem k- Wert mit
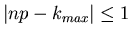 . Der Funktionswert im Maximum
ergibt sich zu
. Der Funktionswert im Maximum
ergibt sich zu
Eine weitere Approximation kann eingeführt werden durch
Wir entwickeln nach Potenzen von x und erhalten
Für  erhalten wir die zweite Approximation
erhalten wir die zweite Approximation
 |
(11) |
mit
 Wie man durch numerisches Rechnen leicht zeigen
kann, spielt der
Wie man durch numerisches Rechnen leicht zeigen
kann, spielt der 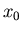 - Term im allgemeinen keine Rolle, sodaß wir auch
- Term im allgemeinen keine Rolle, sodaß wir auch
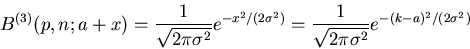 |
(12) |
setzen können. Diese letzteren Funktionen 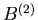 und
und 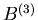 nennt
man auch Gauß- Funktionen. Für große Werte von n und k- Werte in der
Nähe des Maximums (
nennt
man auch Gauß- Funktionen. Für große Werte von n und k- Werte in der
Nähe des Maximums (
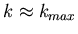 ) geht also die Bernoulli-
Verteilung in die Gauß- Verteilung über.
) geht also die Bernoulli-
Verteilung in die Gauß- Verteilung über.
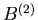 und
und 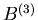 sind für n=20 und p=0.2 in Tabelle 2 aufgelistet.
Wie man sieht, sind diese Approximationen symmetrisch um den wahrscheinlichsten
Wert
sind für n=20 und p=0.2 in Tabelle 2 aufgelistet.
Wie man sieht, sind diese Approximationen symmetrisch um den wahrscheinlichsten
Wert
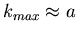 . Daher können diese Funktionen die Bernoulli-
Verteilung nicht in den unsymmetrischen Ausläufern für große und
kleine
. Daher können diese Funktionen die Bernoulli-
Verteilung nicht in den unsymmetrischen Ausläufern für große und
kleine  - Werte beschreiben. Besser stimmen die Bernoulli- Verteilung
und die Gaußsche Approximation
- Werte beschreiben. Besser stimmen die Bernoulli- Verteilung
und die Gaußsche Approximation  für große Werte von n
überein.
für große Werte von n
überein.
Simulation der Bernoulli- Verteilung
Wir können jetzt die Bernoulli- Verteilung durch eine sogenannte
Simulation bestimmen. Dazu führen wir den Versuch V, der uns zur
Definition der Bernoulli- Verteilung geführt hat, im Ereignisraum unseres
Zufallszahlen- Generators durch. Wir bezeichnen den einmaligen Aufruf des
Generators als Einzelversuch 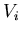 . Dieser Aufruf liefert uns eine Zahl
im Intervall [0,1]. Wir definieren das Ereignis
. Dieser Aufruf liefert uns eine Zahl
im Intervall [0,1]. Wir definieren das Ereignis  durch
durch

Da die vom Generator erzeugten Zufallszahlen gleichverteilt sind, ist dann
offenbar die Wahrscheinlichkeit im Einzelversuch durch
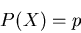
gegeben. Wir führen n derartige Einzelversuche 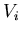 aus, indem wir den
Generator n- mal aufrufen. Wir zählen die Anzahl
aus, indem wir den
Generator n- mal aufrufen. Wir zählen die Anzahl  der Versuche,
in denen das Ereignis
der Versuche,
in denen das Ereignis  eingetroffen ist. Dieses ergibt dann den
Gesamtversuch V. Wir definieren wie bisher als Meßwert der Wahrscheinlichkeit
im Versuch V
eingetroffen ist. Dieses ergibt dann den
Gesamtversuch V. Wir definieren wie bisher als Meßwert der Wahrscheinlichkeit
im Versuch V
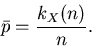
Die einmalige Ausführung des Versuches V liefert natürlich auch nur einen
Wert  bzw.
bzw. 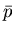 . Führen wir nun den Versuch V beliebig
häufig aus, z.B. M- mal, so erhalten wir bei jedem Versuch eine Zahl
. Führen wir nun den Versuch V beliebig
häufig aus, z.B. M- mal, so erhalten wir bei jedem Versuch eine Zahl

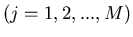 . Wir bezeichnen die Häufigkeit eines
möglichen
. Wir bezeichnen die Häufigkeit eines
möglichen  - Wertes in den M Versuchen mit
- Wertes in den M Versuchen mit 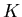 . Die Zahlen
. Die Zahlen 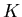 sollten
dann nach der Bernoulli- Formel verteilt sein, d.h.
sollten
dann nach der Bernoulli- Formel verteilt sein, d.h.
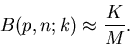
Für die Übungen haben wir ein einfaches Java Programm geschrieben, das diesen
soeben beschriebenen Sachverhalt simuliert.
Tabelle:
Simulationsprogramm und Berechnung der Bernoulli- Verteilung
für n=20 und p=0.2.
| |
M |
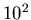 |
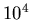 |
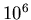 |
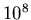 |
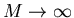 |
| k |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 0 |
|
0.02 |
0.0100 |
0.011586 |
0.011551 |
0.011529 |
| 1 |
|
0.04 |
0.0601 |
0.057492 |
0.057612 |
0.057646 |
| 2 |
|
0.21 |
0.1448 |
0.137091 |
0.136897 |
0.136909 |
| 3 |
|
0.18 |
0.2007 |
0.205006 |
0.205387 |
0.205364 |
| 4 |
|
0.16 |
0.2158 |
0.218123 |
0.218143 |
0.218199 |
| 5 |
|
0.22 |
0.1679 |
0.174831 |
0.174634 |
0.174560 |
| 6 |
|
0.10 |
0.1123 |
0.109178 |
0.109095 |
0.109100 |
| 7 |
|
0.05 |
0.0526 |
0.054584 |
0.054544 |
0.054550 |
| 8 |
|
0.02 |
0.0254 |
0.022207 |
0.022156 |
0.022161 |
| 9 |
|
|
0.0085 |
0.007345 |
0.007387 |
0.007387 |
| 10 |
|
|
0.0017 |
0.001986 |
0.002031 |
0.002031 |
| 11 |
|
|
0.0002 |
0.000471 |
0.000461 |
0.000462 |
| 12 |
|
|
|
0.000085 |
0.000087 |
0.000087 |
| 13 |
|
|
|
0.000012 |
0.000013 |
0.000013 |
| 14 |
|
|
|
0.000003 |
0.000002 |
0.000002 |
|
Simulationsrechnungen beanspruchen
im allgemeinen sehr hohe Rechenzeiten, da die Genauigkeit der Ergebnisse
von der Anzahl M der simulierten Versuche V abhängt. Für die Ergebnisse
in Tabelle 3 wurden bis zu 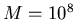 Versuche durchgeführt, um die
Bernoulli- Verteilung für n=20 und p=0.2 zu simulieren. Der Vergleich mit den exakten
Werten aus Tabelle 2 zeigt, daß wir mit dieser bereits relativ großen
Zahl M von Versuchen erst eine Übereinstimmung in der vierten Nachkommastelle
erreicht haben.
Man sollte also, wenn immer es geht, zunächst versuchen,
Probleme analytisch zu lösen. Erst wenn man klar erkannt hat, daß es
keine analytische Lösung gibt, sollte man auf eine Simulation zurückgreifen.
Und auch innerhalb der Simulation können Teilaspekte analytisch gelöst
werden. Die Optimierung von analytischen Problemlösungen und Lösungen mit
Hilfe einer Simulation ist das Hauptanliegen dieses Tutorials. Wir werden
später eine Simulation der Bernoulli- Verteilung kennenlernen,
die wesentlich schneller in der Rechenzeit ist.
Versuche durchgeführt, um die
Bernoulli- Verteilung für n=20 und p=0.2 zu simulieren. Der Vergleich mit den exakten
Werten aus Tabelle 2 zeigt, daß wir mit dieser bereits relativ großen
Zahl M von Versuchen erst eine Übereinstimmung in der vierten Nachkommastelle
erreicht haben.
Man sollte also, wenn immer es geht, zunächst versuchen,
Probleme analytisch zu lösen. Erst wenn man klar erkannt hat, daß es
keine analytische Lösung gibt, sollte man auf eine Simulation zurückgreifen.
Und auch innerhalb der Simulation können Teilaspekte analytisch gelöst
werden. Die Optimierung von analytischen Problemlösungen und Lösungen mit
Hilfe einer Simulation ist das Hauptanliegen dieses Tutorials. Wir werden
später eine Simulation der Bernoulli- Verteilung kennenlernen,
die wesentlich schneller in der Rechenzeit ist.
Fehler Integral und Standard Abweichung
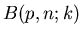 gibt also, um es noch mal zu sagen, die Wahrscheinlichkeit an,
in n Versuchen k-mal das Ereignis
gibt also, um es noch mal zu sagen, die Wahrscheinlichkeit an,
in n Versuchen k-mal das Ereignis  zu finden, wenn
zu finden, wenn 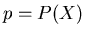 die
Wahrscheinlichkeit für das Ereignis
die
Wahrscheinlichkeit für das Ereignis  im Einzelversuch ist.
Im allgemeinen interessiert man sich nicht dafür, wie groß die
Wahrscheinlichkeit für ein bestimmtes
im Einzelversuch ist.
Im allgemeinen interessiert man sich nicht dafür, wie groß die
Wahrscheinlichkeit für ein bestimmtes  ist, sondern dafür, wie
groß die Wahrscheinlichkeit dafür ist, daß
ist, sondern dafür, wie
groß die Wahrscheinlichkeit dafür ist, daß  in einem Intervall von
in einem Intervall von
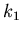 bis
bis 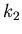 liegt. In diesem Fall muß man die Wahrscheinlichkeiten
für das Intervall
liegt. In diesem Fall muß man die Wahrscheinlichkeiten
für das Intervall ![$[k_{1},k_{2}]$](img82.gif) addieren. Dieses ergibt dann tatsächlich
die Gesamtwahrscheinlichkeit, da, wie wir oben ausgeführt haben,
addieren. Dieses ergibt dann tatsächlich
die Gesamtwahrscheinlichkeit, da, wie wir oben ausgeführt haben, 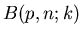 die Wahrscheinlichkeiten von Elementarereignissen
die Wahrscheinlichkeiten von Elementarereignissen 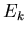 sind und somit
sind und somit
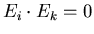 für
für 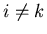 . Daher können wir schreiben
. Daher können wir schreiben
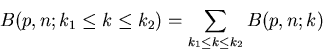 |
(13) |
Interessieren wir uns insbesondere für ein symmetrisches Intervall
um den wahrscheinlichsten Wert
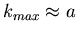 ,
,
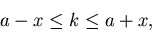 |
(14) |
dann gilt
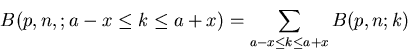 |
(15) |
Mit Hilfe der Approximation 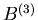 können wir schreiben
können wir schreiben
Wir ersetzen die Summe durch ein Integral und ersetzen die Integrationsvariable
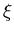 durch
durch 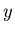 mit Hilfe der Substitution
mit Hilfe der Substitution
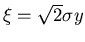 .
Weiterhin drücken wir die Variable
.
Weiterhin drücken wir die Variable 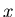 durch Vielfache des Parameters
durch Vielfache des Parameters
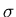 aus,
aus,
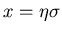 . Nach kurzer Rechnung ergibt sich
. Nach kurzer Rechnung ergibt sich
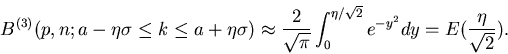 |
(16) |
Das rechts stehende Integral nennt man das Fehler- Integral und den
Parameter 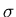 die Standard- Abweichung. Das Fehler- Integral
wird häufig geschrieben als
die Standard- Abweichung. Das Fehler- Integral
wird häufig geschrieben als
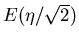 . Mit diesen Definitionen
erhalten wir die Aussage:
. Mit diesen Definitionen
erhalten wir die Aussage:
Satz: Die Wahrscheinlichkeit dafür, daß in 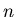 Einzelversuchen
Einzelversuchen  -mal
das Ereignis
-mal
das Ereignis  eintritt, und
eintritt, und  nicht mehr als
nicht mehr als 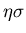 vom
wahrscheinlichsten Wert
vom
wahrscheinlichsten Wert 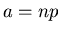 abweicht, ist in der Gaußschen Approximation
unabhängig von n und p und durch
abweicht, ist in der Gaußschen Approximation
unabhängig von n und p und durch
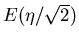 gegeben.
gegeben.
Tabelle:
BASIC- Programm und Berechnung des Fehler- Integrals für 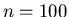 und
und 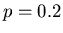 .
.
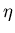 |
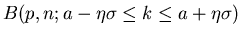 |
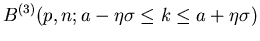 |
| |
|
|
| 0.5 |
0.467744 |
0.382925 |
| 1.0 |
0.740141 |
0.682689 |
| 1.5 |
0.897255 |
0.866386 |
| 2.0 |
0.967405 |
0.954500 |
| 2.5 |
0.991607 |
0.987581 |
| 3.0 |
0.998173 |
0.997300 |
| 3.5 |
0.999645 |
0.999534 |
| 4.0 |
0.999938 |
0.999937 |
|
Wir vergleichen den exakten Ausdruck
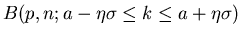 mit der approximativen
Formel
mit der approximativen
Formel
 in Tabelle 4.
in Tabelle 4.
Messung der Wahrscheinlichkeit
Nach diesen Betrachtungen sind wir in der Lage, die Wahrscheinlichkeit
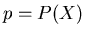 für das Eintreffen des Ereignisses
für das Eintreffen des Ereignisses  im Einzelversuch
im Einzelversuch 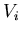 experimentell zu messen. Hierzu führen wir den Versuch
experimentell zu messen. Hierzu führen wir den Versuch 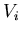 mit
jeweils demselben Bedingungskomplex n- mal aus und zählen die
Häufigkeit
mit
jeweils demselben Bedingungskomplex n- mal aus und zählen die
Häufigkeit  des Eintreffens des Ereignisses
des Eintreffens des Ereignisses  in n Versuchen.
Der wahrscheinlichste Wert
in n Versuchen.
Der wahrscheinlichste Wert 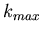 liegt in der Nähe von
liegt in der Nähe von 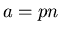 .
Wir definieren daher als Meßwert:
.
Wir definieren daher als Meßwert:
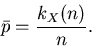 |
(17) |
Wir schreiben den gemessenen Wert in der Form
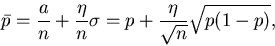 |
(18) |
wobei es fast sicher ist, daß 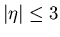 ist (siehe Tabelle 4).
Im vorigen Ausdruck ist
ist (siehe Tabelle 4).
Im vorigen Ausdruck ist 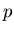 der axiomatisch postulierte Wert (oder auch
der sogenannte wahre Wert) der Wahrscheinlichkeit. Wir lösen diese
Gleichung nach
der axiomatisch postulierte Wert (oder auch
der sogenannte wahre Wert) der Wahrscheinlichkeit. Wir lösen diese
Gleichung nach 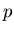 auf und erhalten
auf und erhalten
Vernachlässigen wir Terme mit 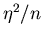 , so folgt
, so folgt
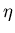 kann positive wie negative Werte annehmen, sodaß wir auch schreiben
können
kann positive wie negative Werte annehmen, sodaß wir auch schreiben
können
 |
(19) |
Als Fehler der Messung bezeichnet man im allgemeinen die einfache Standard-
Abweichung, d.h. für 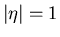 . Wir können also sagen:
. Wir können also sagen:
Mit einer Wahrscheinlichkeit von 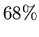 ist der wahre Wert der
Wahrscheinlickeit durch
ist der wahre Wert der
Wahrscheinlickeit durch
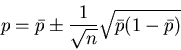 |
(20) |
gegeben, wobei 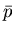 der gemessene Wert ist.
der gemessene Wert ist.
Approximiert man noch
 und beachtet (17), dann
folgt auch
und beachtet (17), dann
folgt auch
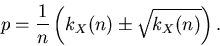 |
(21) |
Dieses beweist das bekannte Gesetz, daß der Fehler einer Zählrate durch die Wurzel der
Zählrate gegeben ist.
Poisson- Verteilung
Die Gaußschen Approximationen beschreiben die Bernoulli- Verteilung nicht
besonders gut für extrem kleine p- Werte. Schon für p=0.2 und n=20 hatten
wir signifikante Abweichungen bei kleinen k- Werten beobachtet (siehe Tabelle).
Um für
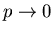 eine meßbare Häufigkeit zu erhalten,
muß in diesem Fall eine sehr große Zahl von Versuchen durchgeführt
werden (
eine meßbare Häufigkeit zu erhalten,
muß in diesem Fall eine sehr große Zahl von Versuchen durchgeführt
werden (
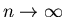 ). Wir nehmen also an, daß zwar
). Wir nehmen also an, daß zwar
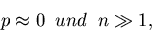 |
(22) |
daß aber das Produkt aus beiden weder verschwindet noch beliebig groß
wird, d.h.
 |
(23) |
Tabelle:
Vergleich der exakten Bernoulli- Verteilung und der Poisson-
Approximation für n=200 und p=0.02.
 |
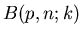 |
 |
| |
|
|
| 0 |
0.017588 |
0.018316 |
| 1 |
0.071788 |
0.073263 |
| 2 |
0.145773 |
0.146525 |
| 3 |
0.196347 |
0.195367 |
| 4 |
0.197349 |
0.195367 |
| 5 |
0.157879 |
0.156293 |
| 6 |
0.104716 |
0.104196 |
| 7 |
0.059277 |
0.059540 |
| 8 |
0.029160 |
0.029770 |
| 9 |
0.012696 |
0.013231 |
| 10 |
0.004949 |
0.005292 |
| 11 |
0.001744 |
0.001925 |
| 12 |
0.000561 |
0.000642 |
| 13 |
0.000165 |
0.000197 |
| 14 |
0.000045 |
0.000056 |
| 15 |
0.000011 |
0.000015 |
| 16 |
0.000003 |
0.000004 |
|
Wir schreiben die Bernoulli- Formel in der Form
Im Limes
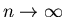 gilt
gilt
und daher
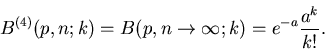 |
(24) |
Dieses ist eine Poisson- Verteilung und 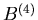 nennt man
die Poisson- Approximation für kleine
nennt man
die Poisson- Approximation für kleine 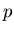 - Werte. Für n=200 und
p=0.02 werden die Funktionswerte der Bernoulli- Verteilung und der
Poisson- Approximation in Tabelle 5 miteinander verglichen. Wir
beobachten eine relativ gute Übereinstimmung für den gesamten
Wertebereich.
- Werte. Für n=200 und
p=0.02 werden die Funktionswerte der Bernoulli- Verteilung und der
Poisson- Approximation in Tabelle 5 miteinander verglichen. Wir
beobachten eine relativ gute Übereinstimmung für den gesamten
Wertebereich.
Ein Java Applet
Für alle Leser, die sich bis hierhin durchgequält haben, jetzt noch zur Belohnung ein
Applet
zum Spielen. Dargestellt ist ein Kartenspiel mit 52 Karten. Ein Versuch
besteht aus 100 Ziehungen einer zufälligen Karte. Die Karte wird nach der Ziehung wieder
in den Kartenstapel zurückgelegt. Im Auswahlmenu Choose können Sie auswählen,
welche Spielkarten als Kopie auf der rechten Seite des Fensters abgelegt werden sollen.
Falls Sie nur die Herzdamen wählen, ist die Erfolgschance pro Zug also
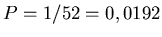 ,
bei 100 Ziehungen erwarten Sie also im Mittel 1,9 Herzdamen. In diesem Fall erhalten Sie
eine Poisson- Verteilung. Bei Wahl aller Damen erhöht sich die Erfolgschance pro Zug
auf
,
bei 100 Ziehungen erwarten Sie also im Mittel 1,9 Herzdamen. In diesem Fall erhalten Sie
eine Poisson- Verteilung. Bei Wahl aller Damen erhöht sich die Erfolgschance pro Zug
auf
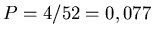 , wir erwarten also etwa 7,7 Damen in 100 Ziehungen. Dieses ergibt eine
typische Binominalverteilung. Akzeptieren wir alle roten Karten, so ist
, wir erwarten also etwa 7,7 Damen in 100 Ziehungen. Dieses ergibt eine
typische Binominalverteilung. Akzeptieren wir alle roten Karten, so ist 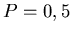 und man kann
die Binominalverteilung durch eine Normalverteilung approximieren. Die Geschwindigkeit der
Animation können Sie im Menu Speed steuern.
und man kann
die Binominalverteilung durch eine Normalverteilung approximieren. Die Geschwindigkeit der
Animation können Sie im Menu Speed steuern.
Aufgaben
Aufgabe 1:
In einer Maschinenhalle arbeiten 10 Maschinen. Die Wahrscheinlichkeit dafür,
daß eine Maschine im Laufe des Tages ausfällt, sei 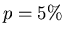 . Die Maschinen
mögen unabhängig voneinander arbeiten. Wie groß ist die Wahrscheinlichkeit
dafür, daß mindestens noch 5 Maschinen am Ende des Tages arbeiten?
. Die Maschinen
mögen unabhängig voneinander arbeiten. Wie groß ist die Wahrscheinlichkeit
dafür, daß mindestens noch 5 Maschinen am Ende des Tages arbeiten?
Aufgabe 2:
Bei der Familienplanung wünscht man sich im allgemeinen genauso viele
Jungens wie Mädchens. Aus der Gesamtbevölkerungsstatistik weiß man,
daß im Mittel von 100 Kindern 55 Jungens und 45 Mädchen geboren werden.
Wie groß sind die Wahrscheinlichkeiten dafür, bei 4 Kindern genau
| a) |
4 Jungens; |
|
| b) |
3 Jungens, |
1 Mädchen; |
| c) |
2 Jungens, |
2 Mädchen; |
| d) |
1 Junge, |
3 Mädchen; |
| e) |
|
4 Mädchen; |
zu bekommen?
Aufgabe 3:
In einem zur Aussenwelt hermetisch abgeriegelten Gasvolumen 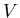 befinden sich
befinden sich
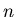 Atome. Für jedes einzelne Atom ist die Aufenthaltswahrscheinlichkeit
über das gesamte Gasvolumen gleich groß und nicht von der Position der
übrigen Atome abhängig.
Atome. Für jedes einzelne Atom ist die Aufenthaltswahrscheinlichkeit
über das gesamte Gasvolumen gleich groß und nicht von der Position der
übrigen Atome abhängig.
a) Wie groß ist die Wahrscheinlichkeit dafür, bei einer Messung der
Anzahlen der Atome genau  Atome in der einen und
Atome in der einen und 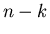 Atome in der
anderen Hälfte des Gasvolumens zu finden?
Atome in der
anderen Hälfte des Gasvolumens zu finden?
b) Bei einer zweiten Messung der Atomzahlen bringen Sie eine kleine Sonde
mit dem Volumen 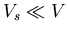 in das Gasvolumen. Berechnen Sie mit Hilfe
eines Computer- Programms die Wahrscheinlichkeitsverteilung der zu
erwartenden Meßwerte für
in das Gasvolumen. Berechnen Sie mit Hilfe
eines Computer- Programms die Wahrscheinlichkeitsverteilung der zu
erwartenden Meßwerte für  ,
, 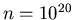 und
und
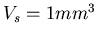 .
.
Aufgabe 4:
In einer radioaktivenn Quelle befinden sich zur Zeit 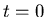 genau
genau 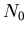 radioaktive Atome. Der Zerfall dieser Atome ist unabhängig voneinander
und die Wahrscheinlichkeit dafür, daß ein bestimmtes Atom zur Zeit
radioaktive Atome. Der Zerfall dieser Atome ist unabhängig voneinander
und die Wahrscheinlichkeit dafür, daß ein bestimmtes Atom zur Zeit 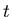 noch nicht zerfallen ist, ist durch
noch nicht zerfallen ist, ist durch
gegeben.
a) Wie groß ist die Wahrscheinlichkeit dafür, zur Zeit 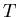 genau
genau 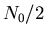 noch nicht zerfallende Atome vorzufinden?
noch nicht zerfallende Atome vorzufinden?
b) Angenommen, Sie bestimmen zur Zeit 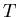 die Anzahl der noch nicht
zerfallenden Atome
die Anzahl der noch nicht
zerfallenden Atome 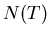 durch eine Messung. Geben Sie für diese Messung
den Fehler als Funktion des Parameters
durch eine Messung. Geben Sie für diese Messung
den Fehler als Funktion des Parameters 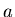 an.
an.
Harm Fesefeldt
2005-03-16
![]()
![]() bei 2 Versuchen ist in der rechten Spalte der Tabelle
aufgeführt. Hieraus ergibt sich
bei 2 Versuchen ist in der rechten Spalte der Tabelle
aufgeführt. Hieraus ergibt sich
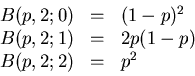

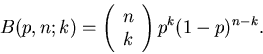
![]() besteht aus n Einzelversuchen
besteht aus n Einzelversuchen ![]()
![]() . Wir definieren die Ereignisse
. Wir definieren die Ereignisse ![]() dadurch, daß
wir sagen,
dadurch, daß
wir sagen, ![]() ist eingetreten, wenn bei n Einzelversuchen k- mal
das Ereignis
ist eingetreten, wenn bei n Einzelversuchen k- mal
das Ereignis ![]() eintritt. Die Ereignisse
eintritt. Die Ereignisse ![]()
![]() sind paarweise unvereinbar, sind also ein Satz von Elementarereignissen.
Wir ordnen jedem Elementarereignis
sind paarweise unvereinbar, sind also ein Satz von Elementarereignissen.
Wir ordnen jedem Elementarereignis ![]() eine Wahrscheinlichkeit
eine Wahrscheinlichkeit
![]() zu. Diese kann gemäß (2) durch die Wahrscheinlichkeit
zu. Diese kann gemäß (2) durch die Wahrscheinlichkeit
![]() für das Auftreten des Ereignisses
für das Auftreten des Ereignisses ![]() im Einzelversuch
ausgedrückt werden.
im Einzelversuch
ausgedrückt werden.
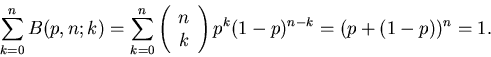
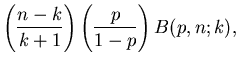
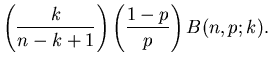

![]() zunächst
nur für gerade Zahlen definiert ist. Eine Interpolationsformel
für reelle Zahlen erhält man mit Hilfe der Stirlingschen Formel
zunächst
nur für gerade Zahlen definiert ist. Eine Interpolationsformel
für reelle Zahlen erhält man mit Hilfe der Stirlingschen Formel
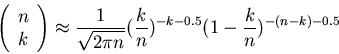

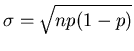
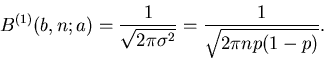
![]() und
und ![]() sind für n=20 und p=0.2 in Tabelle 2 aufgelistet.
Wie man sieht, sind diese Approximationen symmetrisch um den wahrscheinlichsten
Wert
sind für n=20 und p=0.2 in Tabelle 2 aufgelistet.
Wie man sieht, sind diese Approximationen symmetrisch um den wahrscheinlichsten
Wert
![]() . Daher können diese Funktionen die Bernoulli-
Verteilung nicht in den unsymmetrischen Ausläufern für große und
kleine
. Daher können diese Funktionen die Bernoulli-
Verteilung nicht in den unsymmetrischen Ausläufern für große und
kleine ![]() - Werte beschreiben. Besser stimmen die Bernoulli- Verteilung
und die Gaußsche Approximation
- Werte beschreiben. Besser stimmen die Bernoulli- Verteilung
und die Gaußsche Approximation ![]() für große Werte von n
überein.
für große Werte von n
überein.
![]() . Dieser Aufruf liefert uns eine Zahl
im Intervall [0,1]. Wir definieren das Ereignis
. Dieser Aufruf liefert uns eine Zahl
im Intervall [0,1]. Wir definieren das Ereignis ![]() durch
durch
![]() gibt also, um es noch mal zu sagen, die Wahrscheinlichkeit an,
in n Versuchen k-mal das Ereignis
gibt also, um es noch mal zu sagen, die Wahrscheinlichkeit an,
in n Versuchen k-mal das Ereignis ![]() zu finden, wenn
zu finden, wenn ![]() die
Wahrscheinlichkeit für das Ereignis
die
Wahrscheinlichkeit für das Ereignis ![]() im Einzelversuch ist.
Im allgemeinen interessiert man sich nicht dafür, wie groß die
Wahrscheinlichkeit für ein bestimmtes
im Einzelversuch ist.
Im allgemeinen interessiert man sich nicht dafür, wie groß die
Wahrscheinlichkeit für ein bestimmtes ![]() ist, sondern dafür, wie
groß die Wahrscheinlichkeit dafür ist, daß
ist, sondern dafür, wie
groß die Wahrscheinlichkeit dafür ist, daß ![]() in einem Intervall von
in einem Intervall von
![]() bis
bis ![]() liegt. In diesem Fall muß man die Wahrscheinlichkeiten
für das Intervall
liegt. In diesem Fall muß man die Wahrscheinlichkeiten
für das Intervall ![]() addieren. Dieses ergibt dann tatsächlich
die Gesamtwahrscheinlichkeit, da, wie wir oben ausgeführt haben,
addieren. Dieses ergibt dann tatsächlich
die Gesamtwahrscheinlichkeit, da, wie wir oben ausgeführt haben, ![]() die Wahrscheinlichkeiten von Elementarereignissen
die Wahrscheinlichkeiten von Elementarereignissen ![]() sind und somit
sind und somit
![]() für
für ![]() . Daher können wir schreiben
. Daher können wir schreiben
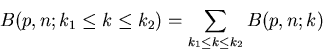
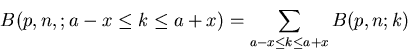
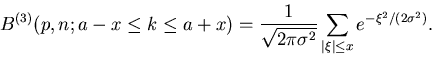
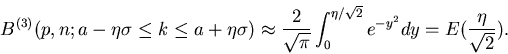
![]() mit der approximativen
Formel
mit der approximativen
Formel
![]() in Tabelle 4.
in Tabelle 4.
![]() für das Eintreffen des Ereignisses
für das Eintreffen des Ereignisses ![]() im Einzelversuch
im Einzelversuch ![]() experimentell zu messen. Hierzu führen wir den Versuch
experimentell zu messen. Hierzu führen wir den Versuch ![]() mit
jeweils demselben Bedingungskomplex n- mal aus und zählen die
Häufigkeit
mit
jeweils demselben Bedingungskomplex n- mal aus und zählen die
Häufigkeit ![]() des Eintreffens des Ereignisses
des Eintreffens des Ereignisses ![]() in n Versuchen.
Der wahrscheinlichste Wert
in n Versuchen.
Der wahrscheinlichste Wert ![]() liegt in der Nähe von
liegt in der Nähe von ![]() .
Wir definieren daher als Meßwert:
.
Wir definieren daher als Meßwert:


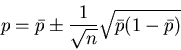
![]() und beachtet (17), dann
folgt auch
und beachtet (17), dann
folgt auch
![]() eine meßbare Häufigkeit zu erhalten,
muß in diesem Fall eine sehr große Zahl von Versuchen durchgeführt
werden (
eine meßbare Häufigkeit zu erhalten,
muß in diesem Fall eine sehr große Zahl von Versuchen durchgeführt
werden (
![]() ). Wir nehmen also an, daß zwar
). Wir nehmen also an, daß zwar
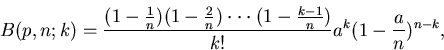
![]() ,
bei 100 Ziehungen erwarten Sie also im Mittel 1,9 Herzdamen. In diesem Fall erhalten Sie
eine Poisson- Verteilung. Bei Wahl aller Damen erhöht sich die Erfolgschance pro Zug
auf
,
bei 100 Ziehungen erwarten Sie also im Mittel 1,9 Herzdamen. In diesem Fall erhalten Sie
eine Poisson- Verteilung. Bei Wahl aller Damen erhöht sich die Erfolgschance pro Zug
auf
![]() , wir erwarten also etwa 7,7 Damen in 100 Ziehungen. Dieses ergibt eine
typische Binominalverteilung. Akzeptieren wir alle roten Karten, so ist
, wir erwarten also etwa 7,7 Damen in 100 Ziehungen. Dieses ergibt eine
typische Binominalverteilung. Akzeptieren wir alle roten Karten, so ist ![]() und man kann
die Binominalverteilung durch eine Normalverteilung approximieren. Die Geschwindigkeit der
Animation können Sie im Menu Speed steuern.
und man kann
die Binominalverteilung durch eine Normalverteilung approximieren. Die Geschwindigkeit der
Animation können Sie im Menu Speed steuern.
![]() . Die Maschinen
mögen unabhängig voneinander arbeiten. Wie groß ist die Wahrscheinlichkeit
dafür, daß mindestens noch 5 Maschinen am Ende des Tages arbeiten?
. Die Maschinen
mögen unabhängig voneinander arbeiten. Wie groß ist die Wahrscheinlichkeit
dafür, daß mindestens noch 5 Maschinen am Ende des Tages arbeiten?
![]() befinden sich
befinden sich
![]() Atome. Für jedes einzelne Atom ist die Aufenthaltswahrscheinlichkeit
über das gesamte Gasvolumen gleich groß und nicht von der Position der
übrigen Atome abhängig.
Atome. Für jedes einzelne Atom ist die Aufenthaltswahrscheinlichkeit
über das gesamte Gasvolumen gleich groß und nicht von der Position der
übrigen Atome abhängig. ![]() Atome in der einen und
Atome in der einen und ![]() Atome in der
anderen Hälfte des Gasvolumens zu finden?
Atome in der
anderen Hälfte des Gasvolumens zu finden? ![]() in das Gasvolumen. Berechnen Sie mit Hilfe
eines Computer- Programms die Wahrscheinlichkeitsverteilung der zu
erwartenden Meßwerte für
in das Gasvolumen. Berechnen Sie mit Hilfe
eines Computer- Programms die Wahrscheinlichkeitsverteilung der zu
erwartenden Meßwerte für ![]() ,
, ![]() und
und
![]() .
.
![]() genau
genau ![]() radioaktive Atome. Der Zerfall dieser Atome ist unabhängig voneinander
und die Wahrscheinlichkeit dafür, daß ein bestimmtes Atom zur Zeit
radioaktive Atome. Der Zerfall dieser Atome ist unabhängig voneinander
und die Wahrscheinlichkeit dafür, daß ein bestimmtes Atom zur Zeit ![]() noch nicht zerfallen ist, ist durch
noch nicht zerfallen ist, ist durch