Zufällige Prozesse
Definition des zufälligen Prozesses
Das Beispiel der Vielfachstreuung im vorherigen Abschnitt führt uns direkt zum
Begriff des zufälligen Prozesses.
Wir gehen daher jetzt einen Schritt weiter und diskutieren zufällige Prozesse.
Ein zufälliger Prozeß wird vollkommen analog zur Definition der
zufälligen Veränderlichen eingeführt. Gegeben sei ein Ereignisraum
mit endlich vielen oder abzählbar unendlich vielen Elementarereignissen
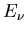 .
Wir ordnen jedem Elementarereignis
.
Wir ordnen jedem Elementarereignis 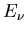 eine Funktion
eine Funktion 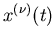 zu. Diese Zuordnung kann, ähnlich wie bei der Abbildung der Ereignisse auf
eine zufällige Veränderliche, durch die Zuordnung
zu. Diese Zuordnung kann, ähnlich wie bei der Abbildung der Ereignisse auf
eine zufällige Veränderliche, durch die Zuordnung
 |
(1) |
beschrieben werden. Man schreibt auch hier symbolisch:
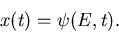 |
(2) |
Man muß also klar unterscheiden: Eine zufällige Veränderliche wurde
definiert durch eine Abbildung des Ereignisraumes auf eine Teilmenge der
reellen Zahlen, ein zufälliger Prozeß wird definiert durch eine
Abbildung des Ereignisraumes auf eine Menge von Funktionen.
Einfache Beispiele von zufälligen Prozessen sind:
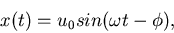 |
(3) |
wobei 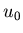 eine zufällige Veränderliche ist. Ein solchen Prozess können wir im ersten
Applet
studieren. Öffnen Sie hierzu das Auswahlmenu Process und wählen Sie Process1.
Weiterhin öffnen Sie das Fenster View. Es erscheint ein Bildschirm, auf dem ein Strom
mit zufälligen Werten für
eine zufällige Veränderliche ist. Ein solchen Prozess können wir im ersten
Applet
studieren. Öffnen Sie hierzu das Auswahlmenu Process und wählen Sie Process1.
Weiterhin öffnen Sie das Fenster View. Es erscheint ein Bildschirm, auf dem ein Strom
mit zufälligen Werten für 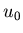 ,
, 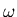 und
und 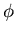 gezeigt wird. In dem Auswahlfenster
Plot haben Sie die Möglichkeit, zu 4 verschieden Zeiten Time1, Time2, Time3 und Time4
sich die Verteilung des Stromes anzeigen zu lassen. Diese Zeiten sind auf dem Bildschirm als rote
Linien dargestellt. Man erhält ersichtlich zu allen Zeiten die gleiche Verteilung. Auf die Verteilungen
mit den Bezeichnungen Correlation 1 und CorrelationFunction werden wir noch am Ende dieses
Abschnittes zurückkommen.
gezeigt wird. In dem Auswahlfenster
Plot haben Sie die Möglichkeit, zu 4 verschieden Zeiten Time1, Time2, Time3 und Time4
sich die Verteilung des Stromes anzeigen zu lassen. Diese Zeiten sind auf dem Bildschirm als rote
Linien dargestellt. Man erhält ersichtlich zu allen Zeiten die gleiche Verteilung. Auf die Verteilungen
mit den Bezeichnungen Correlation 1 und CorrelationFunction werden wir noch am Ende dieses
Abschnittes zurückkommen.
Allgemeiner kann ein Prozess auch durch
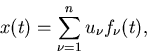 |
(4) |
dargestellt werden, wobei die  die Komponenten eines zufälligen Vektors
die Komponenten eines zufälligen Vektors
 sind und die
sind und die 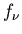 irgendwelche
irgendwelche
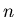 Funktionen sind.
Funktionen sind.
In den beiden vorhergehenden Beispielen konnten wir den zufälligen
Prozeß  als gegeben ansehen, wenn die Dichtefunktion
der zufälligen Veränderlichen
als gegeben ansehen, wenn die Dichtefunktion
der zufälligen Veränderlichen 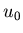 in (3) bzw die Dichtefunktion
des zufälligen Vektors
in (3) bzw die Dichtefunktion
des zufälligen Vektors 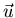 in (4) bekannt sind. Zufällige
Prozesse sind aber im allgemeinen nicht so einfach darstellbar wie
in den beiden obigen Beispielen. Wir verallgemeinern daher und sagen:
in (4) bekannt sind. Zufällige
Prozesse sind aber im allgemeinen nicht so einfach darstellbar wie
in den beiden obigen Beispielen. Wir verallgemeinern daher und sagen:
Ein zufälliger Prozeß  ist als gegeben anzusehen,
wenn für beliebige Zeiten
ist als gegeben anzusehen,
wenn für beliebige Zeiten 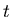 die Dichtefunktionen
die Dichtefunktionen 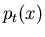 der
zufälligen Veränderlichen
der
zufälligen Veränderlichen 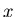 bekannt sind. Hierbei können die
bekannt sind. Hierbei können die
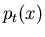 für verschiedene Zeiten
für verschiedene Zeiten 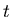 durchaus verschiedene
Dichtefunktionen sein.
durchaus verschiedene
Dichtefunktionen sein.
Um es nochmal mit anderen Worten zu sagen: Bei einem Versuch können
endlich viele oder abzählbar unendlich viele Funktionen  als
Ergebnis des Versuches auftreten. Handelt es sich hierbei um zufällige
Ereignisse, so nennen wir
als
Ergebnis des Versuches auftreten. Handelt es sich hierbei um zufällige
Ereignisse, so nennen wir  einen zufälligen Prozeß. Wir führen
jetzt einen Zeitschnitt ein und betrachten
einen zufälligen Prozeß. Wir führen
jetzt einen Zeitschnitt ein und betrachten  zu einer festen Zeit
zu einer festen Zeit 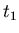 .
. 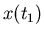 ist dann eine
zufällige Veränderliche mit der Dichtefunktion
ist dann eine
zufällige Veränderliche mit der Dichtefunktion 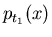 .
Wir betrachten den zufälligen Prozeß als gegeben, wenn die
Dichtefunktionen
.
Wir betrachten den zufälligen Prozeß als gegeben, wenn die
Dichtefunktionen 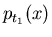 für beliebige Zeiten
für beliebige Zeiten 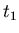 bekannt sind.
bekannt sind.
Die weitere Untersuchung von zufälligen Prozessen basiert damit
weitgehend auf der Untersuchung der zufälligen Veränderlichen 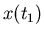 mit der Dichtefunktion
mit der Dichtefunktion 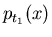 für beliebige, aber feste Zeiten
für beliebige, aber feste Zeiten 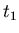 .
.
Beispiele
Zwei einfache Beispiele sollen das Gesagte verdeutlichen. Bei der im vorherigen Abschnitt
behandelten Vielfachstreuung beim Durchgang von Teilchen durch Materie können wir die
Strecke 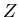 auch durch die Zeit
auch durch die Zeit 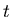 ersetzen, bei konstanter Geschwindigkeit
ersetzen, bei konstanter Geschwindigkeit 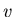 ist dann
ist dann
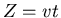 und die Dichtefunktion zur Zeit
und die Dichtefunktion zur Zeit 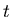 lässt sich schreiben als:
lässt sich schreiben als:
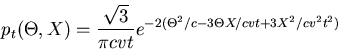 |
(5) |
Im folgenden
Applet
zeigen wir noch einmal die Dichtefunktionen bei verschiedenen Strecken
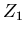 und
und 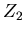 bzw Zeiten
bzw Zeiten 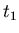 und
und 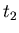 . Öffnen Sie hierzu zunächst im rechten Auswahlfenster
die Wahl x1-x2. Im Hauptfenster sehen Sie dann die Korrelation der Abweichungen der
Teilchenbahn von der geradliniegen Bahn bei den Zeiten
. Öffnen Sie hierzu zunächst im rechten Auswahlfenster
die Wahl x1-x2. Im Hauptfenster sehen Sie dann die Korrelation der Abweichungen der
Teilchenbahn von der geradliniegen Bahn bei den Zeiten 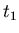 und
und 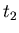 . Zusätzlich
werden zwei Fenster geöffnet, in denen die Verteilung der Abweichungen selbst gezeigt wird.
Beide sind normal verteilt, die Verteilung bei
. Zusätzlich
werden zwei Fenster geöffnet, in denen die Verteilung der Abweichungen selbst gezeigt wird.
Beide sind normal verteilt, die Verteilung bei 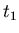 ist offensichtlich schmaler als die
Verteilung bei
ist offensichtlich schmaler als die
Verteilung bei 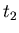 .
.
Ein weiteres Beispiel ist der Rauschstrom an einem Widerstand. Bei konstanter Spannung ist der
Strom bekanntlich durch 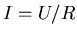 gegeben. Durch Instabilität des Netzes und durch Temperaturschwankungen
erhält man allerdings einen statistisch schwankenden Strom,
gegeben. Durch Instabilität des Netzes und durch Temperaturschwankungen
erhält man allerdings einen statistisch schwankenden Strom,
 |
(6) |
wobei wir den Rauschprozess durch die Dichtefunktion
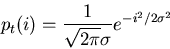 |
(7) |
darstellen können. Insgesamt erhält man in diesem Fall als Dichtefunktion des Stromes 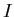 :
:
 |
(8) |
In unserem schon bekannten
Applet
starten Sie jetzt den Prozess Process 2.
Die Dichtefunktion ist normal verteilt und hängt nicht von der Zeit ab. Legen
wir statt der Gleichspannung allerdings eine Wechselpannung an, so wird die Dichtefunktion sehr
wohl von der Zeit abhängen. Die Berechnung solcher Prozesse müssen wir auf ein späteres Kapitel
verschieben, da uns noch die mathematischen Grundlagen fehlen.
Führen wir jetzt in Verallgemeinerung des eben gesagten 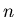 Zeitschnitte
Zeitschnitte
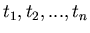 ein und betrachten die
ein und betrachten die 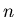 zufälligen
Veränderlichen
zufälligen
Veränderlichen
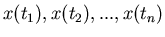 , so bilden diese einen
zufälligen Vektor
, so bilden diese einen
zufälligen Vektor
 .
Wir benutzen die folgenden symbolischen Schreibweisen,
.
Wir benutzen die folgenden symbolischen Schreibweisen,
und schreiben die Dichtefunktion des zufälligen Vektors 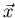 als
als
Wir können dann sagen:
Ein zufälliger Prozeß  ist als gegeben anzusehen, wenn die
Verteilungsfunktionen
ist als gegeben anzusehen, wenn die
Verteilungsfunktionen
 für beliebige Zeiten
für beliebige Zeiten
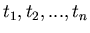 und für beliebige natürliche
Zahlen
und für beliebige natürliche
Zahlen 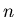 bekannt sind.
bekannt sind.
Momente
Im Sinne der vorherigen Ausführungen definieren wir als gewöhnliches
Moment der Ordnung
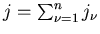 den Mittelwert
den Mittelwert
und als zentrales Moment den Mittelwert
Die Definitionen für Varianzen, Kovarianzen sowie alle Rechenregeln für
die allgemeinen Momente sind vollkommen identisch zu denen des vorgerigen
Kapitels über zufällige Veränderliche und brauchen daher nicht
wiederholt zu werden.
Stationäre zufällige Prozesse
In der Praxis hat man es im allgemeinen nur mit einer sehr eingeschränkten
Klasse von Prozessen zu tun. Wir definieren:
Ein zufälliger Prozeß heißt stationär, wenn für beliebige Zeiten
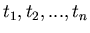 und für ein beliebiges Zeitintervall
und für ein beliebiges Zeitintervall
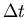 gilt:
gilt:
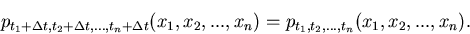 |
(11) |
Man kann also, ohne die Dichtefunktion zu ändern, einen 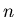 -
dimensionalen Schnitt durch einen stationären zufälligen Prozeß
zeitlich beliebig verschieben, wenn dabei nur die einzelnen zeitlichen
Abstände erhalten bleiben. Wichtig ist in (11) also, daß das Zeitintervall
-
dimensionalen Schnitt durch einen stationären zufälligen Prozeß
zeitlich beliebig verschieben, wenn dabei nur die einzelnen zeitlichen
Abstände erhalten bleiben. Wichtig ist in (11) also, daß das Zeitintervall
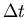 für alle
für alle
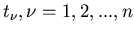 dasselbe ist. Als Gegenbeispiel sei
unser Applet über Vielfachstreung genannt. Die zweite Variable ist hier der Ablenkwinkel
dasselbe ist. Als Gegenbeispiel sei
unser Applet über Vielfachstreung genannt. Die zweite Variable ist hier der Ablenkwinkel
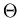 . Die gemeinsamen Dichtefunktion hängt wird in beiden Variablen breiter,
wenn man in der Zeit von
. Die gemeinsamen Dichtefunktion hängt wird in beiden Variablen breiter,
wenn man in der Zeit von 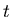 nach
nach  geht. Unser Rauschstrom dagegen ist
stationär.
geht. Unser Rauschstrom dagegen ist
stationär.
Der stationäre Prozeß ist ein Sonderfall des periodischen Prozesses,
zu dessen Definition man gelangt, wenn der Verschiebungsparameter 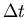 durch
durch 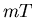 ersetzt wird.
ersetzt wird.  ist die Periodendauer des Prozesses und
ist die Periodendauer des Prozesses und 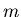 eine natürliche Zahl.
eine natürliche Zahl.
Ein zufälliger Prozeß heißt periodisch mit der Periodendauer  , wenn
für eine beliebige natürliche Zahl
, wenn
für eine beliebige natürliche Zahl 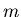 gilt:
gilt:
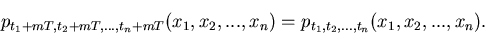 |
(12) |
Ein Sonderfall der stationären Prozesse sind die normalen Prozesse.
Wir definieren:
Ein zufälliger Prozeß  heißt normal, wenn für beliebige Zeiten
heißt normal, wenn für beliebige Zeiten
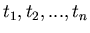 gilt:
gilt:
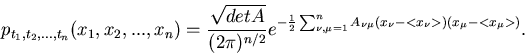 |
(13) |
Wir hatten die 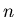 - dimensionale Normalverteilung im vorherigen Unterkapitel
bereits kurz diskutiert. Die Matrix
- dimensionale Normalverteilung im vorherigen Unterkapitel
bereits kurz diskutiert. Die Matrix 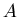 ist hierbei die inverse Matrix der
Kovarianzmatrix,
ist hierbei die inverse Matrix der
Kovarianzmatrix,
Korrelationsfunktion
Bei einem Schnitt durch einen stationären Prozeß  an der Stelle
an der Stelle
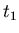 erhalten wir eine eindimensionale Veränderliche
erhalten wir eine eindimensionale Veränderliche
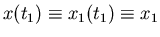 , für deren Dichtefunktion
nach (11) gilt:
, für deren Dichtefunktion
nach (11) gilt:
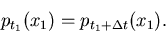 |
(14) |
Wählen wir speziell
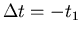 , so folgt
, so folgt
 |
(15) |
Daher: Bei einem stationären Prozeß sind alle eindimensionalen
Dichtefunktionen
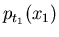 unabhängig von der speziellen Wahl
von
unabhängig von der speziellen Wahl
von 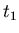 . Für die zweidimensionale Dichtefunktion gilt entsprechend
. Für die zweidimensionale Dichtefunktion gilt entsprechend
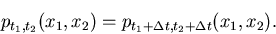 |
(16) |
Setzen wir wieder
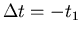 , so gilt
, so gilt
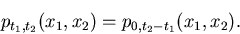 |
(17) |
Daher: Bei einem stationären Prozeß sind alle zweidimensionalen
Dichtefunktionen
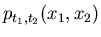 nur von der Zeitdifferenz
nur von der Zeitdifferenz
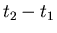 abhängig. Wir lassen im folgenden den Nullindex weg und
schreiben daher
abhängig. Wir lassen im folgenden den Nullindex weg und
schreiben daher
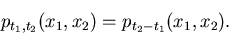 |
(18) |
Wir betrachten jetzt das normale Moment zweiter Ordnung
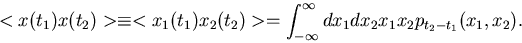 |
(19) |
Da die Dichtefunktion nur von 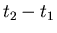 abhängt, können wir setzen
abhängt, können wir setzen
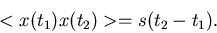 |
(20) |
Man nennt
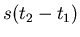 die Korrelationsfunktion des zufälligen
Prozesses
die Korrelationsfunktion des zufälligen
Prozesses  . Man beachte, daß
. Man beachte, daß
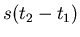 nicht mit der exakten Definition eines Korrelationskoeffizienten
übereinstimmt. Besser wäre die Bezeichnung ,,Momentenfunktion zweiter
Ordnung''. In der technischen Literature hat sich aber der Ausdruck
,,Korrelationsfunktion'' fest eingebürgert.
nicht mit der exakten Definition eines Korrelationskoeffizienten
übereinstimmt. Besser wäre die Bezeichnung ,,Momentenfunktion zweiter
Ordnung''. In der technischen Literature hat sich aber der Ausdruck
,,Korrelationsfunktion'' fest eingebürgert.
Für die Korrelationsfunktion ergeben sich folgende vier Grundeigenschaften:
Die Beweise überlassen wir dem Leser. Aus diesen 4 Eigenschaften läßt
sich der grundsätzliche Verlauf der Korrelationsfunktion, wie in Abb.1
gezeigt, herleiten. Dieses Bild haben wir als Screenshot aus unserem
Applet gewonnen,
wobei wir den Prozess Process 1 und den Plot CorrelationFunction ausgewählt haben.
Die schwarz dargestellten Bereiche stellen hierbei negative Werte dar.
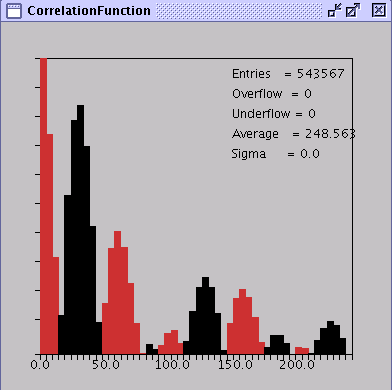
Abbildung 1:
Grundsätzlicher Verlauf der Korrelationsfunktion. Die schwarz dargestellten Werte sind
negative Zahlen.
Integral zufälliger Prozesse
Das Integral über einen zufälligen Prozeß  ,
,
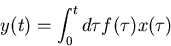 |
(25) |
ergibt einen anderen zufälligen Prozeß 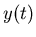 . Die zwei wichtigsten
Regeln sind:
. Die zwei wichtigsten
Regeln sind:
1. In (25) darf die Mittelwertbildung unter dem Integral ausgeführt werden:
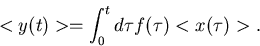 |
(26) |
2. Ist  ein normaler Prozeß, so ist auch
ein normaler Prozeß, so ist auch 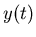 ein normaler Prozeß.
ein normaler Prozeß.
Der Beweis der zweiten Behauptung erfordert die Einführung der erzeugenden
Funktionen und muß daher auf ein späteres Kapitel verschoben
werden.
Aufgaben
Aufgabe 1:
Gegeben sei ein stationärer normaler Prozeß  mit verschwindendem
Mittelwert und der Korrelationsfunktion
mit verschwindendem
Mittelwert und der Korrelationsfunktion
Wie groß ist die Wahrscheinlichkeit dafür, daß  einen Wert annimmt,
der größer als
einen Wert annimmt,
der größer als 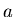 ist?
ist?
Als Zahlenwerte nehmen Sie: 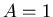 ,
, 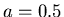 ,
,
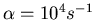 ,
,
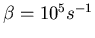 .
.
Aufgabe 2:
Ein experimenteller Versuch gibt zu Beginn eines konstanten Zeitintervalls
 einen Puls mit konstanter Amplitude
einen Puls mit konstanter Amplitude 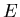 ab. Die Pulslänge
ab. Die Pulslänge 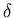 sei mit der Dichtefunktion
sei mit der Dichtefunktion
verteilt. Wie groß ist die Wahrscheinlichkeit dafür, daß sowohl bei
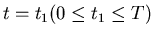 als auch bei
als auch bei 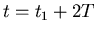 der
Amplitudenwert
der
Amplitudenwert 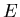 beobachtet wird? Die Richtigkeit Ihrer Lösung können Sie im
Applet
prüfen, wenn Sie den Prozess Process 3 und den Plot Correlation 1 auswählen.
Gezeigt wird dann die gesuchte Funktion
beobachtet wird? Die Richtigkeit Ihrer Lösung können Sie im
Applet
prüfen, wenn Sie den Prozess Process 3 und den Plot Correlation 1 auswählen.
Gezeigt wird dann die gesuchte Funktion
Harm Fesefeldt
2005-03-16
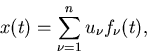
![]() als gegeben ansehen, wenn die Dichtefunktion
der zufälligen Veränderlichen
als gegeben ansehen, wenn die Dichtefunktion
der zufälligen Veränderlichen ![]() in (3) bzw die Dichtefunktion
des zufälligen Vektors
in (3) bzw die Dichtefunktion
des zufälligen Vektors ![]() in (4) bekannt sind. Zufällige
Prozesse sind aber im allgemeinen nicht so einfach darstellbar wie
in den beiden obigen Beispielen. Wir verallgemeinern daher und sagen:
in (4) bekannt sind. Zufällige
Prozesse sind aber im allgemeinen nicht so einfach darstellbar wie
in den beiden obigen Beispielen. Wir verallgemeinern daher und sagen:
![]() ist als gegeben anzusehen,
wenn für beliebige Zeiten
ist als gegeben anzusehen,
wenn für beliebige Zeiten ![]() die Dichtefunktionen
die Dichtefunktionen ![]() der
zufälligen Veränderlichen
der
zufälligen Veränderlichen ![]() bekannt sind. Hierbei können die
bekannt sind. Hierbei können die
![]() für verschiedene Zeiten
für verschiedene Zeiten ![]() durchaus verschiedene
Dichtefunktionen sein.
durchaus verschiedene
Dichtefunktionen sein.
![]() als
Ergebnis des Versuches auftreten. Handelt es sich hierbei um zufällige
Ereignisse, so nennen wir
als
Ergebnis des Versuches auftreten. Handelt es sich hierbei um zufällige
Ereignisse, so nennen wir ![]() einen zufälligen Prozeß. Wir führen
jetzt einen Zeitschnitt ein und betrachten
einen zufälligen Prozeß. Wir führen
jetzt einen Zeitschnitt ein und betrachten ![]() zu einer festen Zeit
zu einer festen Zeit ![]() .
. ![]() ist dann eine
zufällige Veränderliche mit der Dichtefunktion
ist dann eine
zufällige Veränderliche mit der Dichtefunktion ![]() .
Wir betrachten den zufälligen Prozeß als gegeben, wenn die
Dichtefunktionen
.
Wir betrachten den zufälligen Prozeß als gegeben, wenn die
Dichtefunktionen ![]() für beliebige Zeiten
für beliebige Zeiten ![]() bekannt sind.
bekannt sind.
![]() mit der Dichtefunktion
mit der Dichtefunktion ![]() für beliebige, aber feste Zeiten
für beliebige, aber feste Zeiten ![]() .
.
![]() auch durch die Zeit
auch durch die Zeit ![]() ersetzen, bei konstanter Geschwindigkeit
ersetzen, bei konstanter Geschwindigkeit ![]() ist dann
ist dann
![]() und die Dichtefunktion zur Zeit
und die Dichtefunktion zur Zeit ![]() lässt sich schreiben als:
lässt sich schreiben als:
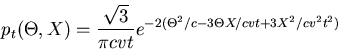
![]() gegeben. Durch Instabilität des Netzes und durch Temperaturschwankungen
erhält man allerdings einen statistisch schwankenden Strom,
gegeben. Durch Instabilität des Netzes und durch Temperaturschwankungen
erhält man allerdings einen statistisch schwankenden Strom,
![]() Zeitschnitte
Zeitschnitte
![]() ein und betrachten die
ein und betrachten die ![]() zufälligen
Veränderlichen
zufälligen
Veränderlichen
![]() , so bilden diese einen
zufälligen Vektor
, so bilden diese einen
zufälligen Vektor
![]() .
Wir benutzen die folgenden symbolischen Schreibweisen,
.
Wir benutzen die folgenden symbolischen Schreibweisen,
![]() den Mittelwert
den Mittelwert

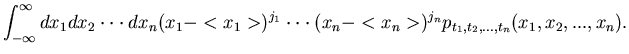
![]() und für ein beliebiges Zeitintervall
und für ein beliebiges Zeitintervall
![]() gilt:
gilt:
![]() durch
durch ![]() ersetzt wird.
ersetzt wird. ![]() ist die Periodendauer des Prozesses und
ist die Periodendauer des Prozesses und ![]() eine natürliche Zahl.
eine natürliche Zahl. ![]() , wenn
für eine beliebige natürliche Zahl
, wenn
für eine beliebige natürliche Zahl ![]() gilt:
gilt:
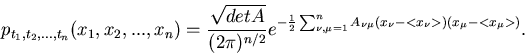
![]() an der Stelle
an der Stelle
![]() erhalten wir eine eindimensionale Veränderliche
erhalten wir eine eindimensionale Veränderliche
![]() , für deren Dichtefunktion
nach (11) gilt:
, für deren Dichtefunktion
nach (11) gilt:
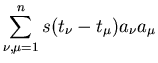

![]() ,
,
![]() mit verschwindendem
Mittelwert und der Korrelationsfunktion
mit verschwindendem
Mittelwert und der Korrelationsfunktion
![]() einen Puls mit konstanter Amplitude
einen Puls mit konstanter Amplitude ![]() ab. Die Pulslänge
ab. Die Pulslänge ![]() sei mit der Dichtefunktion
sei mit der Dichtefunktion