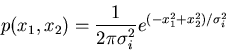Zufällige Veränderliche
Dichtefunktion
Im Mittelpunkt unserer bisherigen Erläuterungen stand der Ereignisraum
mit endlich oder unendlich vielen Elementarereignissen  .
Jedem dieser Elementarereignisse konnten wir eine Wahrscheinlichkeit
.
Jedem dieser Elementarereignisse konnten wir eine Wahrscheinlichkeit
 zuordnen. Die Gesamtheit dieser Zahlenwerte heißt
Wahrscheinlichkeitsverteilung. Es bleibt aber noch eine Besonderheit
zu diskutieren, nämlich die Abbildung der Elementarereignisse
zuordnen. Die Gesamtheit dieser Zahlenwerte heißt
Wahrscheinlichkeitsverteilung. Es bleibt aber noch eine Besonderheit
zu diskutieren, nämlich die Abbildung der Elementarereignisse  auf eine Zahlenskala
auf eine Zahlenskala 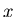 . Diese Abbildung ist natürlich wichtig, wenn man
mit den Wahrscheinlichkeiten analytisch rechnen will oder wenn man die
Wahrscheinlichkeitsverteilung graphisch darstellen will. In vielen
Fällen der Statistik ist diese Abbildung
. Diese Abbildung ist natürlich wichtig, wenn man
mit den Wahrscheinlichkeiten analytisch rechnen will oder wenn man die
Wahrscheinlichkeitsverteilung graphisch darstellen will. In vielen
Fällen der Statistik ist diese Abbildung
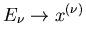 bereits aus dem Problem heraus vorgegeben. Bei unserem Spielwürfel
z.B. wird jedermann die Abbildung
bereits aus dem Problem heraus vorgegeben. Bei unserem Spielwürfel
z.B. wird jedermann die Abbildung
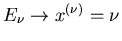 (
(
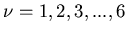 ) durchführen. In diesem Fall geht man in Wahrheit
eigentlich andersherum vor, man definiert die Wahrscheinlichkeiten als
Funktion der zufälligen Veränderlichen
) durchführen. In diesem Fall geht man in Wahrheit
eigentlich andersherum vor, man definiert die Wahrscheinlichkeiten als
Funktion der zufälligen Veränderlichen 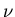 und konstruiert
daraus die logischen Ereignisse. In vielen anderen Fällen ist diese
Abbildung dagegen außerordentlich schwierig zu konstruieren. Als Beispiel
sei das Lottospiel ,,6 aus 49'' erwähnt. Wie soll man 6 beliebige Zahlen
aus 49 möglichen auf eine geordnete Menge von Zahlen abbilden? Das
einzige, was wir mit Sicherheit sagen können, ist, daß der gesamte
Zahlenbereich der Abbildung die Zahlen 1 bis 13983816 umfaßt.
Aber welche Zahlenkombination bezeichnen wir mit der Zahl 1, welche mit der
Zahl 2 usw.? Lassen wir die Besonderheit dieses Beispiels außer acht,
so ergibt sich folgende Situation.
Wir ordnen jedem
und konstruiert
daraus die logischen Ereignisse. In vielen anderen Fällen ist diese
Abbildung dagegen außerordentlich schwierig zu konstruieren. Als Beispiel
sei das Lottospiel ,,6 aus 49'' erwähnt. Wie soll man 6 beliebige Zahlen
aus 49 möglichen auf eine geordnete Menge von Zahlen abbilden? Das
einzige, was wir mit Sicherheit sagen können, ist, daß der gesamte
Zahlenbereich der Abbildung die Zahlen 1 bis 13983816 umfaßt.
Aber welche Zahlenkombination bezeichnen wir mit der Zahl 1, welche mit der
Zahl 2 usw.? Lassen wir die Besonderheit dieses Beispiels außer acht,
so ergibt sich folgende Situation.
Wir ordnen jedem 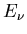 einen Zahlenwert
einen Zahlenwert 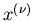 zu. Diese Zuordnung
kann man durch
zu. Diese Zuordnung
kann man durch
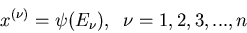 |
(1) |
ausdrücken. Durch diese Zuordnung definieren wir eine zufällige
Veränderliche 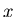 , die mit der Wahrscheinlichkeit
, die mit der Wahrscheinlichkeit 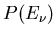 die Werte
die Werte 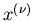 annimmt. Man schreibt symbolisch
annimmt. Man schreibt symbolisch
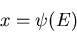 |
(2) |
und meint damit, daß, wenn 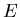 den ,,Wert''
den ,,Wert'' 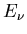 annimmt, nimmt x den
Wert
annimmt, nimmt x den
Wert 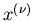 an. Diese Zuordnung kann man verallgemeinern. Ordnet man
jedem Elementarereignis
an. Diese Zuordnung kann man verallgemeinern. Ordnet man
jedem Elementarereignis 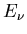 allgemeiner
allgemeiner 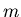 Zahlen zu, so ergibt sich
die Darstellung in Abbildung 1.
Zahlen zu, so ergibt sich
die Darstellung in Abbildung 1.
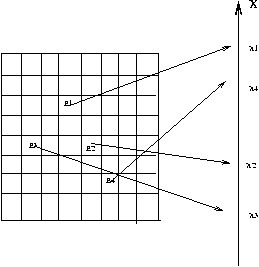
Abbildung 1:
Zuordnung von Ereignis und zufälliger Veränderlicher.
Oder, als Abbildung ausgedrückt,
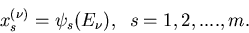 |
(3) |
Jedem Elementarereignis sind also 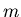 Zahlenwerte zugeordnet, die alle
mit der gleichen Wahrscheinlichkeit auftreten, mit der auch das
Elementarereignis
Zahlenwerte zugeordnet, die alle
mit der gleichen Wahrscheinlichkeit auftreten, mit der auch das
Elementarereignis 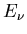 auftritt. Diese Abbildung kann man kürzer
als Vektor schreiben:
auftritt. Diese Abbildung kann man kürzer
als Vektor schreiben:
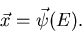 |
(4) |
Darin ist
 ein zufälliger Vektor
oder eine
ein zufälliger Vektor
oder eine 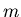 - dimensionale zufällige Veränderliche, die beim Eintreten
des Elementarereignisses
- dimensionale zufällige Veränderliche, die beim Eintreten
des Elementarereignisses 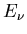 das feste
das feste  -Tupel
-Tupel
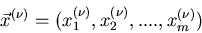
annimmt.
Wie müssen also in der Statistik unterscheiden zwischen zufälligen
Ereignissen und zufälligen Veränderlichen. Ereignisse sind logische
Größen, die mit Hilfe logischer Funktionen verknüpft werden können.
Zufällige Veränderliche sind Größen aus dem Zahlenraum 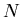 oder
oder 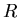 .
Zwischen den Ereignissen und den zufälligen Veränderlichen steht die
Abbildung
.
Zwischen den Ereignissen und den zufälligen Veränderlichen steht die
Abbildung 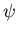 . Die Bedeutung dieser Zuordnung liegt darin, daß mit
ihrer Hilfe die ungeordnete Menge der Elementarereignisse auf eine
geordnete Menge (ganze Zahlen oder reelle Zahlen) abgebildet wird, d.h.
auf eine Menge, in der eine Ordnungsrelation (z.B.
. Die Bedeutung dieser Zuordnung liegt darin, daß mit
ihrer Hilfe die ungeordnete Menge der Elementarereignisse auf eine
geordnete Menge (ganze Zahlen oder reelle Zahlen) abgebildet wird, d.h.
auf eine Menge, in der eine Ordnungsrelation (z.B. 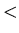 , = oder
, = oder 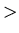 )
definiert ist. Dadurch entsteht ein Ereignisraum mit geordneten
Elementarereignissen. Im Falle eines endlichen Ereignisraumes führt man
diese Abbildung im allgemeinen auf eine Teilmenge der ganzen Zahlen durch,
bei unendlichen Ereignisräumen dagegen auf die Menge der reellen Zahlen.
Die Wahrscheinlichkeitsverteilung
)
definiert ist. Dadurch entsteht ein Ereignisraum mit geordneten
Elementarereignissen. Im Falle eines endlichen Ereignisraumes führt man
diese Abbildung im allgemeinen auf eine Teilmenge der ganzen Zahlen durch,
bei unendlichen Ereignisräumen dagegen auf die Menge der reellen Zahlen.
Die Wahrscheinlichkeitsverteilung 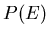 geht dann über in eine
Wahrscheinlichkeitsverteilung für die zufällige Veränderliche
geht dann über in eine
Wahrscheinlichkeitsverteilung für die zufällige Veränderliche 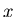 ,
die wir mit
,
die wir mit 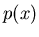 bezeichnen und Dichtefunktion nennen.
Man versucht die Abbildung
bezeichnen und Dichtefunktion nennen.
Man versucht die Abbildung 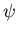 so zu wählen, daß
so zu wählen, daß 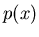 eine stetige
und differenzierbare Funktion wird, bzw. im Falle eines endlichen
Ereignisraumes durch eine einfache Funktion dargestellt werden kann,
die zu einer stetigen und differenzierbaren Funktion erweitert werden kann.
Wie wir später noch genauer ausführen werden, braucht man in der
Simulationstechnik beide Darstellungen, sowohl die Darstellung im
logischen Ereignisraum wie die Darstellung im geordneten Zahlenraum.
Eine kurze Bemerkung zur Schreibweise. Im folgenden werden wir uns
bemühen, Ereignisse und Wahrscheinlichkeiten mit Großbuchstaben,
zufällige Veränderliche und Wahrscheinlichkeitsdichten
dagegen mit Kleinbuchstaben zu schreiben.
eine stetige
und differenzierbare Funktion wird, bzw. im Falle eines endlichen
Ereignisraumes durch eine einfache Funktion dargestellt werden kann,
die zu einer stetigen und differenzierbaren Funktion erweitert werden kann.
Wie wir später noch genauer ausführen werden, braucht man in der
Simulationstechnik beide Darstellungen, sowohl die Darstellung im
logischen Ereignisraum wie die Darstellung im geordneten Zahlenraum.
Eine kurze Bemerkung zur Schreibweise. Im folgenden werden wir uns
bemühen, Ereignisse und Wahrscheinlichkeiten mit Großbuchstaben,
zufällige Veränderliche und Wahrscheinlichkeitsdichten
dagegen mit Kleinbuchstaben zu schreiben.
Wir fassen die Dichtefunktion noch einmal zusammen:
In einem unendlich großen Ereignisraum mit den Elementarereignissen
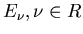 definieren wir eine Abbildung
definieren wir eine Abbildung 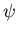 auf die Menge
der reellen Zahlen gemäß
auf die Menge
der reellen Zahlen gemäß
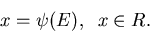 |
(5) |
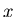 bezeichnen wir als die zugehörige zufällige Veränderliche.
Wir postulieren, daß es eine Dichtefunktion
bezeichnen wir als die zugehörige zufällige Veränderliche.
Wir postulieren, daß es eine Dichtefunktion 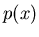 gibt, wobei
gibt, wobei
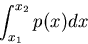 |
(6) |
die Wahrscheinlichkeit ist, die zufällige Veränderliche 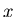 im Intervall
von
im Intervall
von 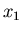 bis
bis 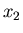 zu finden. Diese Wahrscheinlichkeit ist
prinzipiell nicht bekannt, man kann ihr nur durch Messung der relativen
Häufigkeiten beliebig nahe kommen,
zu finden. Diese Wahrscheinlichkeit ist
prinzipiell nicht bekannt, man kann ihr nur durch Messung der relativen
Häufigkeiten beliebig nahe kommen,
![\begin{displaymath}
h_{x \in [x_{1},x_{2}]} (n) \approx \int_{x_{1}}^{x_{2}} p(x) dx.
\end{displaymath}](img31.gif) |
(7) |
Experimentell mißt man fast immer eine diskrete Häufigkeitsverteilung,
auch wenn die zugehörige Dichtefunktion kontinuierlich ist. Als Beispiel
erwähnen wir die statistische Zählung der Altersstruktur der
Bevölkerung. Hierzu bedient man sich der Einfachheit halber einer
Stichprobe, d.h. man zählt nicht die Altersstruktur der
Gesamtbevölkerung, sondern nur die Altersstruktur einer representativen
Untergruppe. In Abbildung 2 haben wir die relativen Häufigkeiten
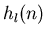 der Menschen mit einem bestimmten Alter
der Menschen mit einem bestimmten Alter 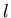 aufgetragen
(
aufgetragen
( ist die Gesamtzahl der Menschen in der Stichprobe).
ist die Gesamtzahl der Menschen in der Stichprobe).
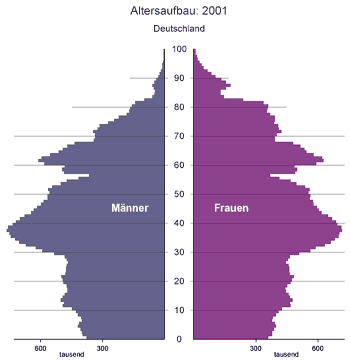
Abbildung 3:
Altersstruktur von Menschen in einer Stichprobe.
Die Dichtefunktion 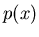 ist aber auch für Menschen mit nicht- ganzzahligem
Alter definiert, und zwar so, daß
ist aber auch für Menschen mit nicht- ganzzahligem
Alter definiert, und zwar so, daß
Wie schon öfters gesagt, die Wahrscheinlichkeiten und damit auch die
Dichtefunktionen sind prinzipiell nicht bekannt. Hier behilft man
sich jetzt häufig eines Modells. Man erstellt aus anderweitigen
theoretischen Überlegungen eine Funktion  , die der
Häufigkeitsverteilung und damit auch der Dichtefunktion möglichst
nahe kommt. Diese Funktion kann im allgemeinen noch von freien Parametern
, die der
Häufigkeitsverteilung und damit auch der Dichtefunktion möglichst
nahe kommt. Diese Funktion kann im allgemeinen noch von freien Parametern
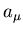 abhängen, sodaß wir schreiben können,
abhängen, sodaß wir schreiben können,
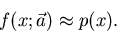 |
(8) |
Wenn wir im folgenden
von Dichtefunktion reden, so meinen wir im allgemeinen die Funktion
 , schreiben aber häufig dafür ebenfalls
, schreiben aber häufig dafür ebenfalls 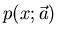 .
Prinzipiell sind aber
.
Prinzipiell sind aber 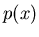 und
und  völlig verschieden. Die Funktion
völlig verschieden. Die Funktion
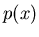 ist durch den Bedingungskomplex des Versuches eindeutig gegeben,
die Funktion
ist durch den Bedingungskomplex des Versuches eindeutig gegeben,
die Funktion  beschreibt gerade das, was wir über den
Bedingungskomplex des Versuches verstanden zu haben glauben.
beschreibt gerade das, was wir über den
Bedingungskomplex des Versuches verstanden zu haben glauben.
Häufig kann man den Ereignisraum auf eine Teilmenge der ganzen Zahlen abbilden:
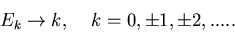 |
(9) |
Man spricht dann von der diskreten Veränderlichen 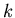 . In diesem Fall
gibt es keine Wahrscheinlichkeitsdichte, sondern nur eine
Wahrscheinlichkeitsverteilung
. In diesem Fall
gibt es keine Wahrscheinlichkeitsdichte, sondern nur eine
Wahrscheinlichkeitsverteilung 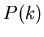 . Eine Wahrscheinlichkeitsdichte
. Eine Wahrscheinlichkeitsdichte
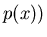 kann durch eine Wahrscheinlichkeitsverteilung
kann durch eine Wahrscheinlichkeitsverteilung 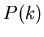 approximiert
werden, indem man die reelle Zahlengerade in geeignet gewählte Intervalle
einteilt und
approximiert
werden, indem man die reelle Zahlengerade in geeignet gewählte Intervalle
einteilt und
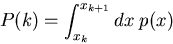 |
(10) |
setzt. Hiervon werden wir später sehr viel Gebrauch machen.
Mittelwerte
Eine zufällige Veränderliche ist gegeben, wenn ihre Dichtefunktion
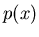 gegeben ist. Diese Funktionen sind aber oft unbekannt und auch
meßtechnisch nur schwer erfaßbar. Es kommt somit darauf an, solche
Parameter der zufälligen Veränderlichen zu finden, die einerseits leicht
gemessen werden können und mit deren Hilfe andererseits auf die
Dichtefunktion
gegeben ist. Diese Funktionen sind aber oft unbekannt und auch
meßtechnisch nur schwer erfaßbar. Es kommt somit darauf an, solche
Parameter der zufälligen Veränderlichen zu finden, die einerseits leicht
gemessen werden können und mit deren Hilfe andererseits auf die
Dichtefunktion 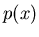 bzw. auf die Modellfunktion
bzw. auf die Modellfunktion 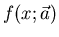 geschlossen werden kann. Solche Parameter sind teils sehr einfache,
häufig aber auch komplizierte Mittelwerte der Veränderlichen, die man
allgemein als Momente bezeichnet. Wir beginnen mit dem einfachen
Mittelwert.
geschlossen werden kann. Solche Parameter sind teils sehr einfache,
häufig aber auch komplizierte Mittelwerte der Veränderlichen, die man
allgemein als Momente bezeichnet. Wir beginnen mit dem einfachen
Mittelwert.
Sind 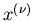 (
(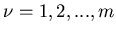 ) mögliche Zahlenergebnisse eines
Versuches V, d.h. sind die
) mögliche Zahlenergebnisse eines
Versuches V, d.h. sind die 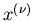 die aus den Elementarereignissen
die aus den Elementarereignissen
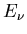 hergeleiteten Veränderlichen, und sind
hergeleiteten Veränderlichen, und sind 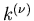 die
gemessenen Häufigkeiten für die Ergebnisse
die
gemessenen Häufigkeiten für die Ergebnisse 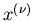 , so nennt man
, so nennt man
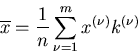 |
(11) |
den arithmetischen Mittelwert. Hierbei ist
die Gesamtzahl der durchgeführten Versuche. Für sehr große
Versuchszahlen  stabilisiert sich die relative Häufigkeit
stabilisiert sich die relative Häufigkeit
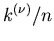 des Zahlenwertes
des Zahlenwertes 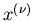 in der Nähe der
Wahrscheinlichkeit
in der Nähe der
Wahrscheinlichkeit  . Dann gilt
. Dann gilt
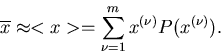 |
(12) |
Ist 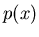 eine stetige Funktion, so können wir auch schreiben
eine stetige Funktion, so können wir auch schreiben
 |
(13) |
Wir bezeichnen mit 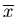 den arithmetischen Mittelwert einer
Stichprobe, mit
den arithmetischen Mittelwert einer
Stichprobe, mit 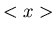 den mathematischen Erwartungswert. Man beachte die verschiedenen Bedeutungen des Querstriches über einer
Größe in der Statistik. Bei zufälligen Ereignissen bedeutet es das
komplementäre Ereignis, bei zufälligen Veränderlichen dagegen
den arithmetischen Mittelwert. Beides hat offensichtlich nichts
miteinander zu tun.
den mathematischen Erwartungswert. Man beachte die verschiedenen Bedeutungen des Querstriches über einer
Größe in der Statistik. Bei zufälligen Ereignissen bedeutet es das
komplementäre Ereignis, bei zufälligen Veränderlichen dagegen
den arithmetischen Mittelwert. Beides hat offensichtlich nichts
miteinander zu tun.
Für eine diskrete Veränderliche 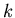 wird der Erwartungswert entsprechend
durch
wird der Erwartungswert entsprechend
durch
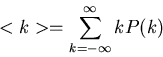 |
(14) |
definiert. Für die Normierungen gilt
Dieses drückt die Tatsache aus, daß die Wahrscheinlichkeit für das
Eintreten irgendeines Ereignisses gleich 1 sein muß.
Im folgenden schreiben wir alle Formeln nur für stetige Veränderliche 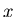 .
Die entsprechenden Formeln für diskrete Veränderliche erhält man mit der
einfachen Ersetzung
.
Die entsprechenden Formeln für diskrete Veränderliche erhält man mit der
einfachen Ersetzung
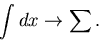 |
(17) |
Momente
Man versteht unter einem Moment einen verallgemeinerten Mittelwert
nach folgender Definition. Gegeben sei eine  - dimensionale zufällige
Veränderliche
- dimensionale zufällige
Veränderliche
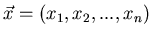 mit der Dichtefunktion
mit der Dichtefunktion
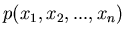 . Dann ist ein gewöhnliches Moment der
Ordnung
. Dann ist ein gewöhnliches Moment der
Ordnung
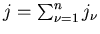 der Mittelwert
der Mittelwert
 |
(18) |
und das zentrale Moment der Ordnung
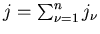 der
Mittelwert
der
Mittelwert
Die wichtigsten Momente sind einmal die eigentlichen Mittelwerte
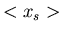 selbst, sowie die beiden quadratischen zentralen Momente
selbst, sowie die beiden quadratischen zentralen Momente
Die erstere nennt man die Varianz oder Dispersion. Sie ist ein Maß für die
Stärke der Streuung der Werte von 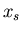 um den Mittelwert
um den Mittelwert 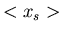 .
Die Kovarianz
.
Die Kovarianz
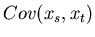 ist eine wichtige Größe bei der
Untersuchung der statistischen Unabhängigkeit der Veränderlichen
ist eine wichtige Größe bei der
Untersuchung der statistischen Unabhängigkeit der Veränderlichen
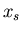 und
und 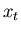 . Auf diese Größe werden wir später in diesem
Kapitel bei der Erläuterung des Korrelationskoeffizienten noch detailierter
eingehen.
. Auf diese Größe werden wir später in diesem
Kapitel bei der Erläuterung des Korrelationskoeffizienten noch detailierter
eingehen.
Bestimmt man diese Momente aus einer statistischen Stichprobe, so ist
in den vorhergehenden Formeln
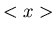 durch
durch 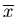 und die Integrale durch Summenbildungen über
die relativen Häufigkeiten zu ersetzen. Man bezeichnet diese Größen
dann als Momente der Stichprobe.
und die Integrale durch Summenbildungen über
die relativen Häufigkeiten zu ersetzen. Man bezeichnet diese Größen
dann als Momente der Stichprobe.
Rechenregeln
Die folgenden Rechenregeln folgen sofort aus der Integral- bzw.
Summendefinition der Erwartungswerte.
1. Sei
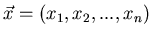 ein Vektor von zufälligen
Veränderlichen mit der Dichtefunktion
ein Vektor von zufälligen
Veränderlichen mit der Dichtefunktion
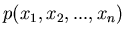 , so
ist
, so
ist
2. Gilt für eine eindimensionale Veränderliche 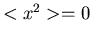 , so ist
die Dichtefunktion durch die Diracsche
, so ist
die Dichtefunktion durch die Diracsche 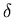 - Funktion gegeben, d.h.
- Funktion gegeben, d.h.
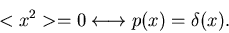 |
(24) |
Diese wichtige und interessante Aussage soll kurz bewiesen werden.
Ist 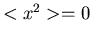 , so kann
, so kann 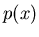 nur für
nur für 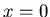 von Null verschieden sein.
Da
von Null verschieden sein.
Da 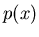 normiert sein muß, d.h.
normiert sein muß, d.h.
erfüllt die Diracsche 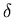 - Funktion die Behauptung. Ist umgekehrt
- Funktion die Behauptung. Ist umgekehrt
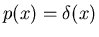 , so ist nach Definition
, so ist nach Definition
Auf Grund der allgemeinen Beziehung
erhalten wir den Beweis der umgekehrten Folgerung.
3. Sind alle Komponenten des zufälligen Vektors
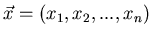 mit der Dichtefunktion
mit der Dichtefunktion
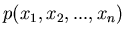 voneinander unabhängig, d.h. wenn gilt,
voneinander unabhängig, d.h. wenn gilt,
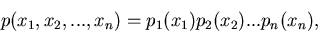 |
(25) |
dann gilt auch
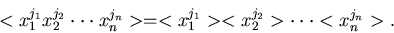 |
(26) |
4. Sind zwei Komponenten 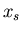 und
und 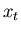 eines Vektors
eines Vektors
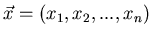 zufälliger Veränderlicher unabhängig
voneinander, d.h. wenn
zufälliger Veränderlicher unabhängig
voneinander, d.h. wenn
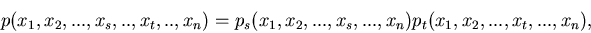 |
(27) |
wobei also  nicht von
nicht von 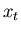 und
und 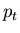 nicht von
nicht von
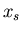 abhängt, dann gilt
abhängt, dann gilt
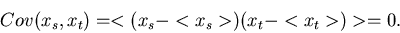 |
(28) |
Für unabhängige Veränderliche 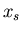 und
und 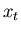 verschwindet die
Kovarianz. Die Umkehrung dieser Behauptung braucht nicht richtig zu
sein.
verschwindet die
Kovarianz. Die Umkehrung dieser Behauptung braucht nicht richtig zu
sein.
5. Sind alle Komponenten des zufälligen Vektors
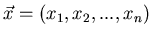 voneinander unabhängig, dann genügt
die Dispersion einer Summe der Identität
voneinander unabhängig, dann genügt
die Dispersion einer Summe der Identität
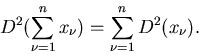 |
(29) |
6. Sind 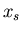 und
und 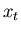 zwei zufällige Veränderliche aus
zwei zufällige Veränderliche aus
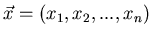 , so gilt die Cauchy-Schwarzsche
Ungleichung
, so gilt die Cauchy-Schwarzsche
Ungleichung
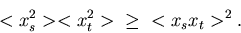 |
(30) |
Korrelationskoeffizient
Ein Maß für die statistische Abhängigkeit zweier zufälliger
Veränderlicher 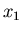 und
und 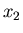 wird durch den
Korrelationskoeffizienten gegeben. Wir definieren diese Größe durch
wird durch den
Korrelationskoeffizienten gegeben. Wir definieren diese Größe durch
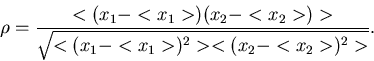 |
(31) |
Der Korrelationskoeffizient hat drei bemerkenswerte Eigenschaften:
1. Für unabhängige Veränderliche 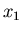 und
und 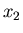 ist
ist
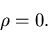 |
(32) |
2. Der Korrelationskoeffizient genügt stets der Ungleichung
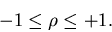 |
(33) |
Der Beweis erfolgt mit Hilfe der Cauchy-Schwarzschen Ungleichung.
3. Ist 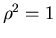 , so sind die Veränderlichen
, so sind die Veränderlichen 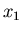 und
und 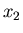 vollständig miteinander korreliert, d.h. es gilt
vollständig miteinander korreliert, d.h. es gilt
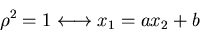 |
(34) |
mit reellen Konstanten 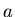 und
und 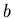 .
.
Kovarianzmatrix
Die Erläuterungen des vorhergehenden Abschnitts können auf
mehrdimensionale Veränderliche
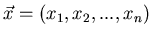 übertragen werden. Stellt man die Kovarianzen
übertragen werden. Stellt man die Kovarianzen
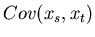 aller Komponentenpaare in einer Matrix zusammen,
aller Komponentenpaare in einer Matrix zusammen,
so gilt der für die Anwendungen wichtige Satz:
Notwendig und hinreichend dafür, daß zwischen den Veränderlichen
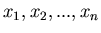 mit
mit
 mindestens eine lineare Beziehung der
Form
mindestens eine lineare Beziehung der
Form
 besteht, ist die Bedingung
besteht, ist die Bedingung
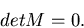 |
(35) |
Dieses ist die Verallgemeinerung der dritten Behauptung des
vorhergehenden Abschnitts.
Die Beweise für die Behauptungen dieses gesamten Abschnitts können
in jedem Lehrbuch der Statistik nachgeschlagen werden.
Transformation von zufälligen Veränderlichen
In den Anwendungen kommt es häufig vor, daß einer gegebenen zufälligen
Veränderlichen 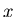 in ganz bestimmter Weise eine neue zufällige
Veränderliche
in ganz bestimmter Weise eine neue zufällige
Veränderliche 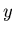 zugeordnet wird, und zwar gemäß einer Abbildung
zugeordnet wird, und zwar gemäß einer Abbildung
 |
(36) |
Wir nehmen an, daß auch die Umkehrfunktion existiert,
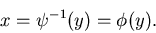 |
(37) |
Die Dichtefunktion 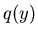 der zufälligen Veränderlichen
der zufälligen Veränderlichen 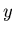 findet man
folgendermaßen. Wegen der Normierung der Dichtefunktion gilt
findet man
folgendermaßen. Wegen der Normierung der Dichtefunktion gilt
und
Daher können wir schreiben
Also ist
 |
(38) |
die Dichtefunktion der zufälligen Veränderlichen 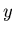 .
.
Dieses Verfahren kann man auf zufällige Vektoren verallgemeinern.
Sei
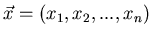 ein Vektor von
ein Vektor von  zufälligen
Veränderlichen und
zufälligen
Veränderlichen und
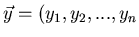 ein anderer Vektor
von
ein anderer Vektor
von  zufälligen Veränderlichen. Seien ferner
zufälligen Veränderlichen. Seien ferner
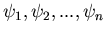 umkehrbar eindeutige Abbildungen,
umkehrbar eindeutige Abbildungen,
mit
dann kann die Dichtefunktion
 aus der
Dichtefunktion
aus der
Dichtefunktion
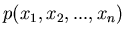 berechnet werden gemäß
berechnet werden gemäß
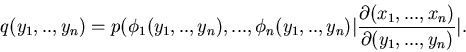 |
(42) |
Die darin auftretende Funktionaldeterminante lautet ausführlich
geschrieben
In (42) ist dann der Betrag dieser Determinante einzusetzen.
Häufig hat man es mit Transformationen der Art
mit 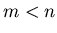 zu tun, d.h. man interessiert sich für die Verteilungsfunktion
eines reduzierten Vektors von zufälligen Veränderlichen. Zur Lösung
erweitern wir die Transformationen mit beliebigen, aber geeignet
gewählten Hilfstransformationen. Die einfachste Wahl ist
zu tun, d.h. man interessiert sich für die Verteilungsfunktion
eines reduzierten Vektors von zufälligen Veränderlichen. Zur Lösung
erweitern wir die Transformationen mit beliebigen, aber geeignet
gewählten Hilfstransformationen. Die einfachste Wahl ist
Dann lautet die Umkehrfunktion:
Die weitere Rechnung geht wie Gleichung (42), nur muß noch über
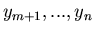 integriert werden:
integriert werden:
Da 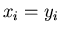 für
für 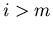 , gilt auch
, gilt auch
und damit
Dieses Integral schreibt man häufig in der saloppen, aber einprägsamen
Form
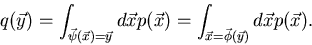 |
(48) |
Die Einfachheit der numerischen Lösung der Transformation hängt manchmal
von der Wahl der Hilfstransformationen ab. Bei einigen Problemen müssen
diese daher verschieden von der Wahl (45) gewählt werden.
Beispiel
In der Simulation kommt es häufig vor, daß man abhängige
Variable 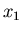 und
und 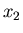 derart transformieren muß, daß die neuen
Variablen
derart transformieren muß, daß die neuen
Variablen 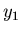 und
und  nicht mehr voneinender abhängig sind.
Sei also
nicht mehr voneinender abhängig sind.
Sei also
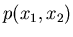 die Dichtefunktion einer zweidimensionalen
Veränderlichen
die Dichtefunktion einer zweidimensionalen
Veränderlichen 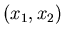 mit
mit
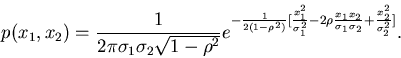 |
(49) |
Man prüft leicht nach, daß 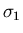 und
und 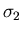 die Varianzen
von
die Varianzen
von 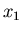 und
und 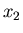 sind und daß
sind und daß  der Korrelationskoeffizient
ist. Der Faktor vor der Exponentialfunktion garantiert die richtige
Normierung,
der Korrelationskoeffizient
ist. Der Faktor vor der Exponentialfunktion garantiert die richtige
Normierung,
Wir schreiben den Ausdruck im Exponenten gemäß
und substituieren
Die Umkehrung ist eindeutig und ergibt
Die Funktionaldeterminante berechnet sich zu
Die transformierte Dichtefunktion lautet schließlich
 |
(50) |
Hierin sind die zufälligen Veränderlichen 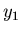 und
und  offensichtlich
unabhängig. Dieses ist eine zweidimensionale Gaußverteilung mit den
Varianzen
offensichtlich
unabhängig. Dieses ist eine zweidimensionale Gaußverteilung mit den
Varianzen
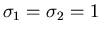 und dem Korrelationskoeffizienten
und dem Korrelationskoeffizienten
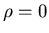 .
.
Eine andere Transformation,
mit
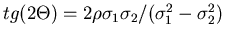 führt auf das gleiche Ergebnis. Diese Transformation ist zwar in ihrer
Abhängigkeit von
führt auf das gleiche Ergebnis. Diese Transformation ist zwar in ihrer
Abhängigkeit von 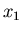 und
und 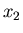 bzw
bzw 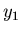 und
und  symmetrischer,
und damit ästhetisch schöner, rechentechnisch jedoch ungünstiger,
da trigonometrische Funktionen auftreten.
symmetrischer,
und damit ästhetisch schöner, rechentechnisch jedoch ungünstiger,
da trigonometrische Funktionen auftreten.
Der Ausdruck (49) stellt eine Normalverteilung um die Erwartungswerte
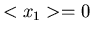 und
und  eines zweidimensionalen Vektors
eines zweidimensionalen Vektors
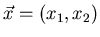 dar. Die Normalverteilung läßt sich auf
dar. Die Normalverteilung läßt sich auf
 - dimensionale Vektoren verallgemeinern:
- dimensionale Vektoren verallgemeinern:
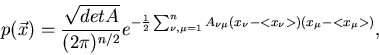 |
(51) |
wobei wir die Matrix
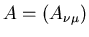 eingeführt haben. Der Ausdruck vor
der Exponentialfunktion garantiert die richtige Normierung,
eingeführt haben. Der Ausdruck vor
der Exponentialfunktion garantiert die richtige Normierung,
Wir werden in einem späteren Kapitel noch detaillierter auf diese Verteilung eingehen. Im
Augenblick soll die Bemerkung genügen, daß die Kovarianzmatrix des
zufälligen Vektors  die zu
die zu 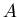 inverse Matrix
inverse Matrix 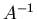 ist, d.h.
ist, d.h.
Man muß also bei gegebener Kovarianzmatrix 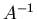 zunächst die inverse
Matrix
zunächst die inverse
Matrix 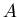 bestimmen, um zu einem expliziten Ausdruck für die Dichtefunktion
von normalverteilten Vektoren zu gelangen.
bestimmen, um zu einem expliziten Ausdruck für die Dichtefunktion
von normalverteilten Vektoren zu gelangen.
Für einen zweidimensionalen Vektor rechnen wir dieses Verfahren einmal
explizit durch. Wir setzen
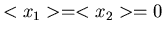 und erhalten
und erhalten
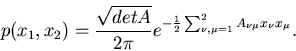 |
(52) |
Die Kovarianzmatrix ist
Wir identifizieren
Daher können wir setzen
Die hierzu inverse Matrix ist, wie man leicht nachrechnen kann,
Einsetzen dieser Matrix in (52) ergibt dann tatsächlich (49).
Anwendung
Als Anwendung betrachten wir ein Beispiel aus der Teilchenphysik. Wenn ein
Teilchen durch Materie dringt, wird es durch vielfache elastische Streuungen
mit den Atomen der Materie aus seiner geradliniegen Bahn abgelengt. Es hat beim
Verlassen der Materieschicht nicht nur eine Richtungsänderung 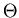 gegenüber
seiner ursprünglichen Richtung, sondern auch einen Versatz
gegenüber
seiner ursprünglichen Richtung, sondern auch einen Versatz 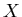 (siehe Abbildung 3).
Die theoretische Behandlung dieses Problems müssen wir auf ein späteres Kapitel
vertagen. Als Ergebnis erhält man
(siehe Abbildung 3).
Die theoretische Behandlung dieses Problems müssen wir auf ein späteres Kapitel
vertagen. Als Ergebnis erhält man
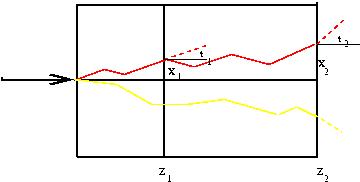
Abbildung 3:
Teilchenbahn unter dem Einfluss der Vielfachstreuung.
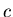 ist hierbei eine materialabhängige Konstante und
ist hierbei eine materialabhängige Konstante und 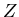 ist die Dicke des Materials.
Die Dichtefunktion in
ist die Dicke des Materials.
Die Dichtefunktion in  und
und 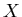 ist (siehe Aufgabe 1):
ist (siehe Aufgabe 1):
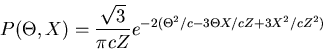 |
(53) |
Im folgenden
Applet
haben wir eine Simulation dieser Vielfachstreuung programmiert.
Beim Laden des Applets wird zunächst die Bahn des Teilchens gezeigt. Im rechten
Auswahlfeld kann man sich sich die simulierten Grössen für 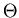 und
und 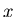 in einem
zweidimensionalen Plot ansehen. Als Erweiterung haben wir auch noch die Möglichkeit,
die Korrelationen für die Ablenkwinkel und Versätze bei zwei Orten
in einem
zweidimensionalen Plot ansehen. Als Erweiterung haben wir auch noch die Möglichkeit,
die Korrelationen für die Ablenkwinkel und Versätze bei zwei Orten 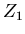 und
und  der Teichenbahn zu untersuchen.
der Teichenbahn zu untersuchen.
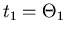 bzw
bzw
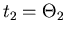 sind dann die Ablenkwinkel bei den Schichtdicken
sind dann die Ablenkwinkel bei den Schichtdicken 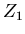 bzw
bzw  ,
, 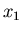 und
und 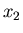 die
entsprechenden Versätze gegenüber der geradliniegen Bahn.
Die Parameter des Teilchens, des Ansorbers
und die Werte für
die
entsprechenden Versätze gegenüber der geradliniegen Bahn.
Die Parameter des Teilchens, des Ansorbers
und die Werte für 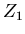 und
und  können im Eingabefeld verändert werden.
Die theoretischen Erwartungswerte für die Messwerte bei verschiedenen Schichtdicken
sind:
können im Eingabefeld verändert werden.
Die theoretischen Erwartungswerte für die Messwerte bei verschiedenen Schichtdicken
sind:
Diese Ergebnisse sind als rote Korrelationsgeraden in die Plots eingezeichnet.
Übungen
Aufgabe 1:
Beweisen Sie die Formel (53) für die zweidimensionale Dichtefunktion in der
Vielfachstreuung.
Aufgabe 2:
Zeichnen Sie die Kurve der Dichtefunktion
a) Berechnen Sie die Wendepunkte. Wie groß ist die Wahrscheinlichkeit
dafür, bei einer Messung der Veränderlichen 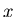 einen Wert zwischen den
Abzissen der Wendepunkte zu erhalten?
einen Wert zwischen den
Abzissen der Wendepunkte zu erhalten?
b) Der Wert für 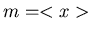 sei bekannt, z.B.
sei bekannt, z.B. 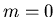 . Berechnen Sie die
Dichtefunktion der zufälligen Veränderlichen
. Berechnen Sie die
Dichtefunktion der zufälligen Veränderlichen 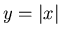 .
.
Aufgabe 3:
Eine zweidimensionale zufällige Veränderliche möge die
Dichtefunktion
besitzen. Wie lauten die Dichtefunktionen der zufälligen Veränderlichen
Aufgabe 4:
Zwei Schützen A und B schießen auf eine Scheibe mit dem Mittelpunkt
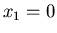 ,
, 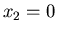 . Die Wahrscheinlichkeit der Einschläge betrage
. Die Wahrscheinlichkeit der Einschläge betrage
mit 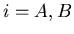 . Sieger ist derjenige Schütze, dessen Schuß den geringsten
Abstand vom Scheibenmittelpunkt hat. Wie groß ist die Wahrscheinlichkeit
dafür, daß
. Sieger ist derjenige Schütze, dessen Schuß den geringsten
Abstand vom Scheibenmittelpunkt hat. Wie groß ist die Wahrscheinlichkeit
dafür, daß 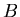 gewinnt?
gewinnt?
Harm Fesefeldt
2005-02-25

![]() oder
oder ![]() .
Zwischen den Ereignissen und den zufälligen Veränderlichen steht die
Abbildung
.
Zwischen den Ereignissen und den zufälligen Veränderlichen steht die
Abbildung ![]() . Die Bedeutung dieser Zuordnung liegt darin, daß mit
ihrer Hilfe die ungeordnete Menge der Elementarereignisse auf eine
geordnete Menge (ganze Zahlen oder reelle Zahlen) abgebildet wird, d.h.
auf eine Menge, in der eine Ordnungsrelation (z.B.
. Die Bedeutung dieser Zuordnung liegt darin, daß mit
ihrer Hilfe die ungeordnete Menge der Elementarereignisse auf eine
geordnete Menge (ganze Zahlen oder reelle Zahlen) abgebildet wird, d.h.
auf eine Menge, in der eine Ordnungsrelation (z.B. ![]() , = oder
, = oder ![]() )
definiert ist. Dadurch entsteht ein Ereignisraum mit geordneten
Elementarereignissen. Im Falle eines endlichen Ereignisraumes führt man
diese Abbildung im allgemeinen auf eine Teilmenge der ganzen Zahlen durch,
bei unendlichen Ereignisräumen dagegen auf die Menge der reellen Zahlen.
Die Wahrscheinlichkeitsverteilung
)
definiert ist. Dadurch entsteht ein Ereignisraum mit geordneten
Elementarereignissen. Im Falle eines endlichen Ereignisraumes führt man
diese Abbildung im allgemeinen auf eine Teilmenge der ganzen Zahlen durch,
bei unendlichen Ereignisräumen dagegen auf die Menge der reellen Zahlen.
Die Wahrscheinlichkeitsverteilung ![]() geht dann über in eine
Wahrscheinlichkeitsverteilung für die zufällige Veränderliche
geht dann über in eine
Wahrscheinlichkeitsverteilung für die zufällige Veränderliche ![]() ,
die wir mit
,
die wir mit ![]() bezeichnen und Dichtefunktion nennen.
Man versucht die Abbildung
bezeichnen und Dichtefunktion nennen.
Man versucht die Abbildung ![]() so zu wählen, daß
so zu wählen, daß ![]() eine stetige
und differenzierbare Funktion wird, bzw. im Falle eines endlichen
Ereignisraumes durch eine einfache Funktion dargestellt werden kann,
die zu einer stetigen und differenzierbaren Funktion erweitert werden kann.
Wie wir später noch genauer ausführen werden, braucht man in der
Simulationstechnik beide Darstellungen, sowohl die Darstellung im
logischen Ereignisraum wie die Darstellung im geordneten Zahlenraum.
Eine kurze Bemerkung zur Schreibweise. Im folgenden werden wir uns
bemühen, Ereignisse und Wahrscheinlichkeiten mit Großbuchstaben,
zufällige Veränderliche und Wahrscheinlichkeitsdichten
dagegen mit Kleinbuchstaben zu schreiben.
eine stetige
und differenzierbare Funktion wird, bzw. im Falle eines endlichen
Ereignisraumes durch eine einfache Funktion dargestellt werden kann,
die zu einer stetigen und differenzierbaren Funktion erweitert werden kann.
Wie wir später noch genauer ausführen werden, braucht man in der
Simulationstechnik beide Darstellungen, sowohl die Darstellung im
logischen Ereignisraum wie die Darstellung im geordneten Zahlenraum.
Eine kurze Bemerkung zur Schreibweise. Im folgenden werden wir uns
bemühen, Ereignisse und Wahrscheinlichkeiten mit Großbuchstaben,
zufällige Veränderliche und Wahrscheinlichkeitsdichten
dagegen mit Kleinbuchstaben zu schreiben.
![]() definieren wir eine Abbildung
definieren wir eine Abbildung ![]() auf die Menge
der reellen Zahlen gemäß
auf die Menge
der reellen Zahlen gemäß

![]() ist aber auch für Menschen mit nicht- ganzzahligem
Alter definiert, und zwar so, daß
ist aber auch für Menschen mit nicht- ganzzahligem
Alter definiert, und zwar so, daß
![]() gegeben ist. Diese Funktionen sind aber oft unbekannt und auch
meßtechnisch nur schwer erfaßbar. Es kommt somit darauf an, solche
Parameter der zufälligen Veränderlichen zu finden, die einerseits leicht
gemessen werden können und mit deren Hilfe andererseits auf die
Dichtefunktion
gegeben ist. Diese Funktionen sind aber oft unbekannt und auch
meßtechnisch nur schwer erfaßbar. Es kommt somit darauf an, solche
Parameter der zufälligen Veränderlichen zu finden, die einerseits leicht
gemessen werden können und mit deren Hilfe andererseits auf die
Dichtefunktion ![]() bzw. auf die Modellfunktion
bzw. auf die Modellfunktion ![]() geschlossen werden kann. Solche Parameter sind teils sehr einfache,
häufig aber auch komplizierte Mittelwerte der Veränderlichen, die man
allgemein als Momente bezeichnet. Wir beginnen mit dem einfachen
Mittelwert.
geschlossen werden kann. Solche Parameter sind teils sehr einfache,
häufig aber auch komplizierte Mittelwerte der Veränderlichen, die man
allgemein als Momente bezeichnet. Wir beginnen mit dem einfachen
Mittelwert.
![]() (
(![]() ) mögliche Zahlenergebnisse eines
Versuches V, d.h. sind die
) mögliche Zahlenergebnisse eines
Versuches V, d.h. sind die ![]() die aus den Elementarereignissen
die aus den Elementarereignissen
![]() hergeleiteten Veränderlichen, und sind
hergeleiteten Veränderlichen, und sind ![]() die
gemessenen Häufigkeiten für die Ergebnisse
die
gemessenen Häufigkeiten für die Ergebnisse ![]() , so nennt man
, so nennt man
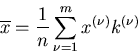
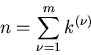
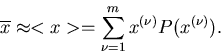
![]() wird der Erwartungswert entsprechend
durch
wird der Erwartungswert entsprechend
durch
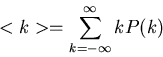
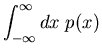
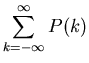
![]() .
Die entsprechenden Formeln für diskrete Veränderliche erhält man mit der
einfachen Ersetzung
.
Die entsprechenden Formeln für diskrete Veränderliche erhält man mit der
einfachen Ersetzung
![]() - dimensionale zufällige
Veränderliche
- dimensionale zufällige
Veränderliche
![]() mit der Dichtefunktion
mit der Dichtefunktion
![]() . Dann ist ein gewöhnliches Moment der
Ordnung
. Dann ist ein gewöhnliches Moment der
Ordnung
![]() der Mittelwert
der Mittelwert
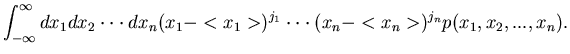
![]() durch
durch ![]() und die Integrale durch Summenbildungen über
die relativen Häufigkeiten zu ersetzen. Man bezeichnet diese Größen
dann als Momente der Stichprobe.
und die Integrale durch Summenbildungen über
die relativen Häufigkeiten zu ersetzen. Man bezeichnet diese Größen
dann als Momente der Stichprobe.
![]() ein Vektor von zufälligen
Veränderlichen mit der Dichtefunktion
ein Vektor von zufälligen
Veränderlichen mit der Dichtefunktion
![]() , so
ist
, so
ist
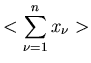

![]() , so ist
die Dichtefunktion durch die Diracsche
, so ist
die Dichtefunktion durch die Diracsche ![]() - Funktion gegeben, d.h.
- Funktion gegeben, d.h.
![]() mit der Dichtefunktion
mit der Dichtefunktion
![]() voneinander unabhängig, d.h. wenn gilt,
voneinander unabhängig, d.h. wenn gilt,
![]() und
und ![]() eines Vektors
eines Vektors
![]() zufälliger Veränderlicher unabhängig
voneinander, d.h. wenn
zufälliger Veränderlicher unabhängig
voneinander, d.h. wenn
![]() voneinander unabhängig, dann genügt
die Dispersion einer Summe der Identität
voneinander unabhängig, dann genügt
die Dispersion einer Summe der Identität
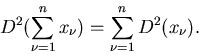
![]() und
und ![]() zwei zufällige Veränderliche aus
zwei zufällige Veränderliche aus
![]() , so gilt die Cauchy-Schwarzsche
Ungleichung
, so gilt die Cauchy-Schwarzsche
Ungleichung
![]() und
und ![]() wird durch den
Korrelationskoeffizienten gegeben. Wir definieren diese Größe durch
wird durch den
Korrelationskoeffizienten gegeben. Wir definieren diese Größe durch
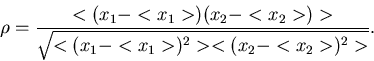
![]() und
und ![]() ist
ist
![]() , so sind die Veränderlichen
, so sind die Veränderlichen ![]() und
und ![]() vollständig miteinander korreliert, d.h. es gilt
vollständig miteinander korreliert, d.h. es gilt
![]() übertragen werden. Stellt man die Kovarianzen
übertragen werden. Stellt man die Kovarianzen
![]() aller Komponentenpaare in einer Matrix zusammen,
aller Komponentenpaare in einer Matrix zusammen,
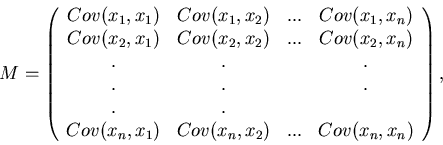
![]() in ganz bestimmter Weise eine neue zufällige
Veränderliche
in ganz bestimmter Weise eine neue zufällige
Veränderliche ![]() zugeordnet wird, und zwar gemäß einer Abbildung
zugeordnet wird, und zwar gemäß einer Abbildung
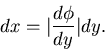
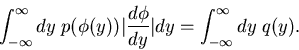

![]() ein Vektor von
ein Vektor von ![]() zufälligen
Veränderlichen und
zufälligen
Veränderlichen und
![]() ein anderer Vektor
von
ein anderer Vektor
von ![]() zufälligen Veränderlichen. Seien ferner
zufälligen Veränderlichen. Seien ferner
![]() umkehrbar eindeutige Abbildungen,
umkehrbar eindeutige Abbildungen,
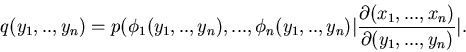
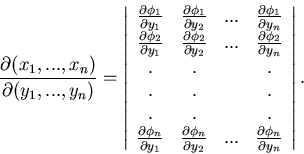
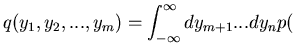
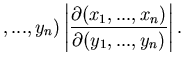
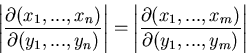
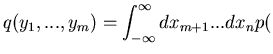
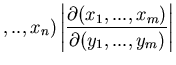
![]() und
und ![]() derart transformieren muß, daß die neuen
Variablen
derart transformieren muß, daß die neuen
Variablen ![]() und
und ![]() nicht mehr voneinender abhängig sind.
Sei also
nicht mehr voneinender abhängig sind.
Sei also
![]() die Dichtefunktion einer zweidimensionalen
Veränderlichen
die Dichtefunktion einer zweidimensionalen
Veränderlichen ![]() mit
mit
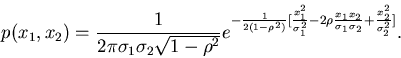
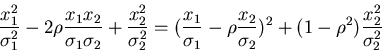
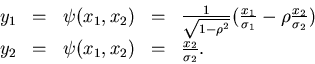
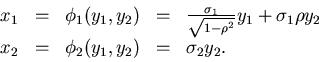
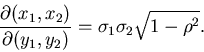
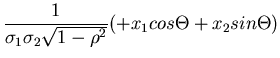
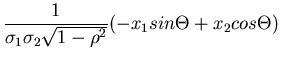
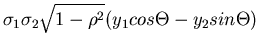
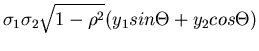
![]() und
und ![]() eines zweidimensionalen Vektors
eines zweidimensionalen Vektors
![]() dar. Die Normalverteilung läßt sich auf
dar. Die Normalverteilung läßt sich auf
![]() - dimensionale Vektoren verallgemeinern:
- dimensionale Vektoren verallgemeinern:
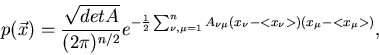
![]() und erhalten
und erhalten
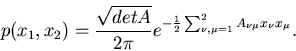
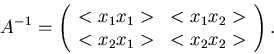
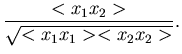
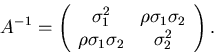
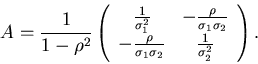
![]() gegenüber
seiner ursprünglichen Richtung, sondern auch einen Versatz
gegenüber
seiner ursprünglichen Richtung, sondern auch einen Versatz ![]() (siehe Abbildung 3).
Die theoretische Behandlung dieses Problems müssen wir auf ein späteres Kapitel
vertagen. Als Ergebnis erhält man
(siehe Abbildung 3).
Die theoretische Behandlung dieses Problems müssen wir auf ein späteres Kapitel
vertagen. Als Ergebnis erhält man

![]() ist hierbei eine materialabhängige Konstante und
ist hierbei eine materialabhängige Konstante und ![]() ist die Dicke des Materials.
Die Dichtefunktion in
ist die Dicke des Materials.
Die Dichtefunktion in ![]() und
und ![]() ist (siehe Aufgabe 1):
ist (siehe Aufgabe 1):
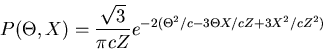

![\begin{displaymath}
p(x_{1},x_{2}) = \frac{1}{2 \pi \sigma_{1} \sigma_{2} \sqrt{...
...\sigma_{1} \sigma_{2}}
+ \frac{x_{2}^{2}}{\sigma_{2}^{2}} ] }
\end{displaymath}](img232.gif)
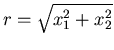 ,
,![]() ,
, ![]() . Die Wahrscheinlichkeit der Einschläge betrage
. Die Wahrscheinlichkeit der Einschläge betrage