This applet illustrates nonrelativistic quantum mechanical scattering from a one-dimensional square potential well of width L and finite energy depth V>0. The well is located between x=0 and x=L, and the incident wave approaches along the negative x axis.

The energy eigenstates are

where k and 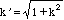are the wavenumbers outside and inside the well, respectively. The e^ikx term is the incident wave, the R term is the reflected wave, and the T term is the transmitted wave.

The unit of distance is chosen such that the state with k=0 has wavenumber

inside the well.

The coefficients are given by

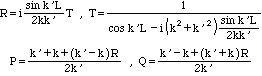
|R|² is the reflection coefficient and |T|² is the transmission coefficient. (They satisfy |R|²+|T|²=1.) The reflection coefficient is given by

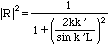
This has maxima at those values of k (the scattering resonances) for which

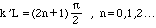
The wavefunction whose probability distribution is animated by the applet has the form

This is a finite sum of energy eigenstates weighted by a Gaussian centered at k₀ with width proportional to Dk. The sum runs in equal steps from k₀-Dk/2 to k₀+Dk/2. A phase factor is included to center the incident wave packet around x=x₀ at t=0. The unit of time is chosen such that the frequency is k²/2.

Notes:

• The location of the well is indicated by the red bar on the graph of the probability density.
• The momentum spectrum is superimposed in blue on the graph of the reflection coefficient.
• The incident wavepacket looks irregular because of interference with the reflected waves.

Instructions for use

• Set the width L of the well (fixed at 30 in the demo) using the scrollbar provided.
• Set the initial position x₀ of the incident wavepacket (fixed at -40 in the demo) using the scrollbar provided.
• Set the number of k values (fixed at 6 in the demo) using the popup menu.
• Set the central momentum k₀ and width Dk using the scrollbars provided.
• Start, stop, resume, and reset using the buttons provided.
• After a run is stopped, any change in parameters resets the time to t=0.